一道关于椭圆中直线恒过定点问题的思考

■河南省商丘市第一高级中学

在圆锥曲线中,椭圆是高考考查的重要内容,其中的定点问题是重点题型之一,值得我们关注。

这类问题的求解策略为:直接推理、计算,并在计算中提取变量,从而得到定点。

下面通过一道例题推导一般结论,再对一般结论进行简要证明。

(1)求椭圆C的方程;

(2)过点A(3,0)作关于x轴对称的两条不同直线l1,l2分别交椭圆C于M(x1,y1)与N(x2,y2),且x1≠x2,证明直线MN恒过x轴上的定点。

解析一:直观设法,从已知两条对称直线入手,根据斜率的关系进行代数化,这种方法找到思路易,但运算难。

故直线MN的方程为:

把②代入③整理得:

解析二:从结论入手,找出直线MN的方程后,直接令y=0,求x即可。

(2)设l1:y=k(x-3),l2:y=-k(x-3)。

解析三:直接设直线MN的方程,此法难想,却易求。

(2)设直线MN的方程x=ny+m(n≠0)。

因为直线l1,l2关于x轴对称,故斜率之和为零。

通过对这道例题的解析,我们可得到如下结论:

证明:设直线AE的方程x=ny+m(n≠0)。

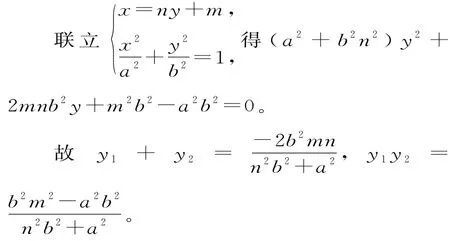
因为直线lEP,lAP关于x轴对称,故其斜率之和为零。

注意:这种解法具有一定的局限性,只适合解决该类问题。