“一网打尽”常用逻辑用语中的参数问题

■江苏省盐城市亭湖区南洋中学

求参数的值或参数的取值范围,是高中数学最常见的一类问题。在常用逻辑用语中也不例外,这类问题比比皆是,随手可得,本文举例说明,供大家参考。

一、与充分条件、必要条件有关的参数问题

这类问题主要有两种情形,一种是根据参数的值判断条件的充分性或必要性;另一种是根据条件的充分性与必要性求参数的取值范围。

例1(1)对于常数m,n,“关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

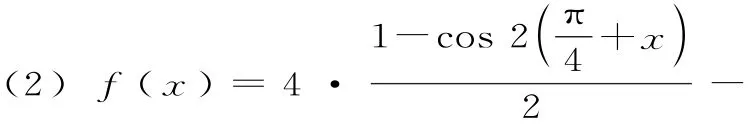
点评:(1)判断不具备充分性或必要性,只需举一个反例说明;(2)根据条件的充分性与必要性求参数的取值范围问题,通常先将其转化为含参数的集合之间的关系,进而转化为不等式问题。

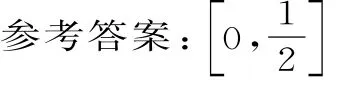
【变式训练1】已知条件p:2x2-3x+1≤0,条件q:x2-(2a+1)x+a(a+1)≤0。若￢p是￢q的必要不充分条件,则实数a的取值范围是 。

二、与逻辑联结词有关的参数问题

这类问题主要指已知复合命题的真假求参数的取值范围,涉及“p∨q”和“p∧q”形式的命题。

例2(1)命题p:对任意实数x,都有ax2+ax+1＞0成立;命题q:关于x的方程x2-x+a=0有实数根。若p∧q为真,则a的取值范围是 。

(2)已知命题p:∃x0∈R,ex0-mx0=0,q:∀x∈R,mx2+mx+1＞0,若p∨(￢q)为假命题,则实数m的取值范围是( )。

A.(-∞,0)∪(4,+∞) B.[0,4]

C.[0,e) D.(0,e)

解析:(1)当p为真命题时,对任意实数x都有ax2+ax+1＞0成立。

(2)由p∨(￢q)为假命题可得p假,q真,若p为假,则ex=mx无解,可得0≤m＜e;若q为真,则0≤m＜4。由[0,e)∩[0,4)=[0,e),故选C。

点评:由复合命题的真假求参数范围问题,一般分三个步骤:首先求出每个简单命题为真时参数的取值范围;再由复合命题的真假确定简单命题的真假情形;最后根据第二步求出满足条件的参数的取值范围。

【变式训练2】已知命题p:∃x0∈R,(m+1)(x20+1)≤0,命题q:∀x∈R,x2+mx+1＞0恒成立,若p∧q为假命题,则实数m的取值范围为 。

参考答案:m≤-2或m＞-1

三、与全称命题、特称命题真假有关的参数问题

例3(1)若命题“∃x0∈R,使得+(1-a)x0+1＜0”是假命题,则实数a的取值范围为 。

(2)已知命题p:“x∈R,m∈R,使4x+2x·m+1=0”,若命题p为真命题,则实数m的取值范围是 。

解析:(1)因为命题“∃x0∈R,使得+(1-a)x0+1＜0”是假命题,所以它的否定“∀x∈R,使得x2+(1-a)x+1≥0”是真命题,故Δ=(a-1)2-4≤0,解得-1≤a≤3,故答案为[-1,3]。

(2)因为命题p为真命题,即方程4x+·m+1=0有实数解,所以≥2,m≤-2,m的取值范围是(-∞,-2]。

点评:(1)已知命题为假命题,则其否定是真命题,故将该题转化为恒成立问题处理。(2)已知命题为真命题,故将该题转化为能成立问题处理。

【变式训练3】已知命题“x∈R,x2-5x的否定为假命题,则实数a的取值范围是 。

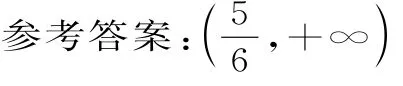
四、与全称量词、特称量词有关的参数问题

这类问题,其实就是含参数的命题恒成立问题与能成立问题,一般可转化为函数的最值问题或值域问题来求参数的取值范围。

(2)当x≥2时,f(x)≥3,g(x)≥a2。

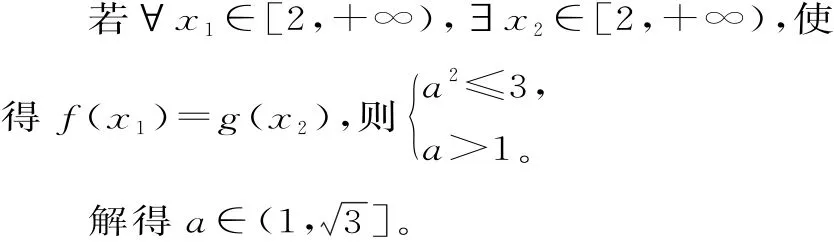
点评:(1)若m=f(x)能成立,则m的取值范围就是函数f(x)的值域;(2)若m≥f(x)(或m≤f(x))恒成立,则m≥f(x)max(或m≤f(x)min)。

A.a≤1 B.a≥1

C.a≤2 D.a≥2

参考答案:A