焦点三角形我为你“点赞”

■湖北省巴东县第三高级中学

椭圆(或双曲线)上任意一点与两焦点的连线构成的三角形称为焦点三角形。焦点三角形,又称“魅力三角形”。

题型一:已知焦点三角形的内角,求解相关问题

例1(2018·全国Ⅱ卷文)已知F1、F2是椭圆C的两个焦点,P是椭圆C上的一点,若PF1⊥PF2,且∠PF2F1=60°,则椭圆C的离心率为( )。

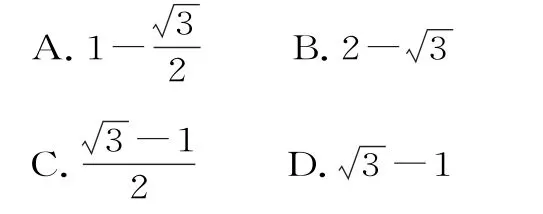
解题思路:设|PF2|=m,利用直角三角形三角函数的定义求|F1F2|、|PF1|,再结合椭圆定义求实轴长,利用离心率计算公式求值。

解析:在 △F1PF2中,∠F1PF2=90°,∠PF2F1=60°。

设|PF2|=m,则2c=|F1F2|=2m,|PF1|=3m。

又由椭圆定义可知2a=|PF1|+|PF2|=+1)m。

点评:椭圆定义的应用主要有两个方面:一是判断平面内动点的轨迹是否为椭圆;二是利用定义求焦点三角形的周长、面积、椭圆的弦长及最值和离心率。

例2(2018·全国Ⅱ卷理)已知F1、F是椭圆2(a＞b＞0)的左、右焦点,A是椭圆C的左顶点,点P在过A且斜率为的直线上,△PFF为等腰三角形,12∠F1F2P=120°,则椭圆C的离心率为( )。

解题思路:等腰三角形的性质求|PF2|、|F1F2|⇒直线斜率的定义、同角三角函数间的关系求sin∠PAF2、cos∠PAF2⇒正弦定理、两角差的正弦公式求a、c关系⇒离心率计算公式求结论。

解析:因为△PF1F2为等腰三角形,∠F1F2P=120°,所以|PF2|=|F1F2|=2c。

点评:求解本题的关键是:①求角∠PAF2的正弦值;②由正弦定理求a、c的关系。

题型二:求焦点三角形的内角或内角的三角函数值

例3(2012·全国Ⅰ卷)已知F1、F2为双曲线C:x2-y2=2的左、右焦点,点P在双曲线C上,|PF1|=2|PF2|,则cos∠F1PF2=( )。

解题思路:设|PF2|=m,则|PF1|=2|PF2|=2m。由双曲线的定义求出m,根据双曲线中a、b、c的关系求2c,再利用余弦定理求cos∠F1PF2。

解析:设|PF2|=m,则|PF1|=2m。

由双曲线定义知|PF1|-|PF2|=2a,所以2m-m=2,m=2。

点评:题目中给定的是等轴双曲线,在“焦点三角形”中,正弦定理、余弦定理、双曲线的定义是经常使用的知识点。

题型三:焦点三角形的内角平分线问题

例4(2011·全国Ⅰ卷)已知F1、F2分别为双曲线C:=1的左、右焦点,点A在双曲线C上,点M的坐标为(2,0),AM为∠F1AF2的平分线,则|AF2|=。

解题思路:先由双曲线的性质求焦点坐标,再由三角形内角平分线定理求,最后由双曲线的定义求|AF2|。

解析:由已知得F1(-6,0),F2(6,0),由三角形内角平分线定理得=2。

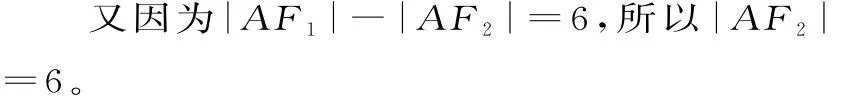
题型四 焦点三角形边的关系问题

例5(2007·湖北卷)双曲线的左准线为l,左焦点和右焦点分别为F1和F2。抛物线C2的准线为l,焦点为F2。双曲线C1与抛物线C2的一个交点为M,则等于( )。

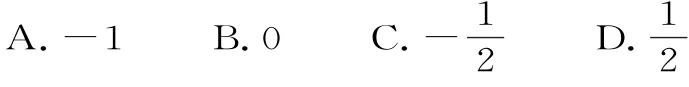
解题思路:设M点在准线l上的射影为点D,由双曲线的定义、抛物线的定义得到关于|MF1|、|MF2|、|MD|的方程组,解方程组求|MF1|、|MF2|,最后代入式子计算

点评:本题是双曲线与抛物线的交汇题,用好双曲线和抛物线的定义,就可顺利解题。

例6(2007·湖北卷)过双曲线1左焦点F的直线交双曲线的左支于

M、N 两点,F2为其右焦点,则|MF2|+|NF2|-|MN|的值为 。

解题思路:妙用双曲线的定义求|MF2|-|MF|、|NF2|-|NF|。

解析:根据双曲线的定义有|MF2|-|MF|=2a,|NF2|-|NF|=2a。

两式相加得|MF2|+|NF2|-|MN|=4a=8。

点评:由双曲线的定义解题时要注意动点的位置,在双曲线的标准方程中,决定焦点位置的因素是x2或y2的系数。