一题攻克解析几何综合问题之弦长

■北京市顺义区第一中学

每次谈及高考数学,大家似乎都有同感:高中数学难,而解析几何又是难中之难。其实只要我们平时注意多思考、多积累、多归纳,就会发现高考题中的解析几何题型稳定,是有规律可循的。只要认真分析就能够找到解题的方法和规律,完全可以让高考数学中的解析几何题,变成让同学们很有信心的得分题目。

解析几何中的弦长问题一般涉及证明题、定值问题、面积问题等,是一类考得最多的解析几何题。下面我们就圆锥曲线中的弦长问题,做深入研究和探讨。

(Ⅰ)求椭圆C的方程。

(Ⅱ)如图1,设直线y=x与椭圆C交于A,B两点,斜率为k的直线l与椭圆交于M,N两点,与直线y=x交于点P(点P与点A,B,M,N不重合)。

(i)当k=-1时,证明:|PA||PB|=|PM||PN|。

图1

所以|PA||PB|=|PM||PN|。

点评:求出A、B、P点坐标,代入两点间距离公式直接计算长度之积

点评:本题考查了椭圆的标准方程,以及向量与几何结合的一些几何性质等基础知识,考查综合运用数学知识进行推理运算的能力。利用法二来做第一问会大大减少运算量,明显提高准确率。对弦长公式的熟练掌握是解决这类问题的关键点。

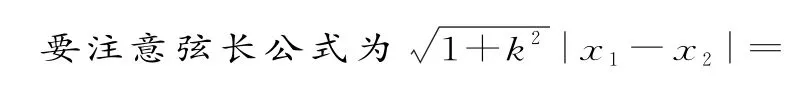
同时,要善于用长度和夹角已知的线段表示未知线段,以达到简化运算的目的。

(1)求椭圆W的方程。

(2)过点A作直线AQ交椭圆W于另一点Q,交y轴于点R。P为椭圆W上一点,且OP∥AQ,直线OP的斜率为k。求证:为定值。

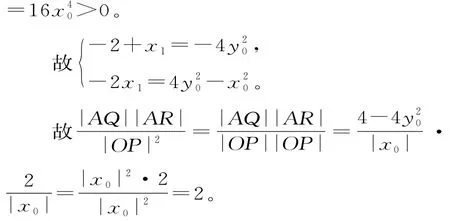
点评:通过本练习题我们可以学到两点:①在直角三角形中长度比与坐标比的转化关系。②直线与椭圆相交时,已知其中一个交点坐标,利用韦达定理求另一个交点坐标(这一技巧会经常在高考中应用)。

纵观近几年高考题,我们会发现解析几何试题的难度,相比前些年下降了不少,选择题、填空题均属中档题,且解答题不再处于压轴题的位置,计算量在减少,但同时要看到思维量还保持着原来的层次和要求,同时加大了与相关知识的联系(如向量、函数、方程等),凸现了教材中研究性学习的能力要求。我们有理由相信自己,只要经过努力,一定会攻克解析几何这一难关的!