高考小题藏乾坤一题九解现真身

■安徽省合肥六中 合肥市中学数学特级教师工作站

2018年新课标全国Ⅰ卷理科第16题是一道在三角背景下求函数最小值的问题,试题设问简洁、构思精巧。命题人的设计初衷应是考查导数在求函数最值中的应用。我们充分挖掘试题内涵,广泛联系数学知识,给出下面九种解法。

题目:已知函数f(x)=2sinx+sin2x,则f(x)的最小值是 。

1.突出导数工具作用,简洁明快

解法一:f(x)的最小正周期为T=2π,只考虑x∈[0,2π)的情形。

评析:上述四种解法都是借助导数这一工具解答的,但处理的细节不一样:解法一最常规,利用周期性将定义域限定在[0,2π)上,通过比较极值和区间端点处函数值的大小来确定函数最小值;解法二将定义域限定在[-π,π)上,并注意到构成函数f(x)的两个函数y=sinx和sin2x的图像特征,发现函数f(x)在上可取到最大值,结合奇函数的中心对称性,得到函数f(x)的最小值,解法二可看作解法一的优化;解法三通过换元、消元将问题转化为一个四次多项式函数,再利用导数来解决;解法四是将函数表达式平方后,通过换元将问题转化为多项式函数解决的。

2.借力于著名不等式,巧妙构造

评析:解法五至解法七是利用四元均值不等式完成解答的。解法五和解法六都对函数解析式作了平方处理,不同点在于解法五直接配凑系数用均值不等式,解法六利用倍角公式变形后再用不等式。解法七借助万能公式将函数解析式用半角的正切表达后直接配凑系数用均值不等式。

图1

3.渗透数形结合思想,形象直观

解法八:如图1所示,在单位圆上,记三点A(-1,0),B(cosx,sinx),C(cos x,-sinx),则 S△ABC=注意到圆的内接三角形中,正三角形面积最大,于是,S△ABC=,故函数的最小值为

图2

要使f(x)=2t取最小值,则需t＜0。如图2所示,当且仅当圆a2+b2=1与双曲线b=-1相切时函数f(x)取得最小值。记切点为P(a0,b0),则

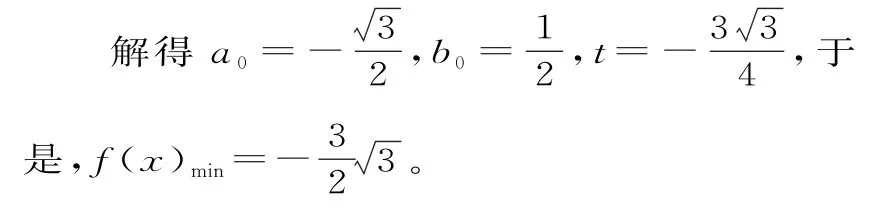
评析:注意到sin2x+cos2x=1可与单位圆自然联系。解法八深入挖掘函数f(x)的几何意义,将其表达成单位圆内接三角形的面积来解决问题。解法九通过换元将问题转化为单位圆与双曲线有公共点的问题,函数f(x)的最小值当且仅当两条曲线相切时取到。

我们看到,上述九个解法或直接研究函数本身的性态,或沟通问题与著名不等式的联系,或构造图形“以形助数”,无论哪种方法,都需要我们仔细分析问题的结构特征,作模式识别,从代数或几何的角度去阐释问题,进而创造性地解决问题。