椭圆两种定义的三种应用

浙江省诸暨工业职业技术学校

运用椭圆的定义解题,主要从三个方面考虑:(1)涉及椭圆上点与两个焦点的距离问题,可借助椭圆的第一定义来转化;(2)涉及椭圆焦点、准线、离心率与曲线上点的有关问题,可借助椭圆的第二定义来转化;(3)同时涉及椭圆的两个焦点与一条准线的有关问题时,可同时借助两个定义来转化。下面举例说明,仅供参考。

一、求椭圆的方程

例1已知圆C1:(x-4)2+y2=169,圆C2:(x+4)2+y2=9,动圆P与圆C1内切,与圆C2外切,求圆心P的轨迹方程。

解析:由平面几何知识知道,两圆相切时可连接两个圆心,利用圆心距与两半径的关系解题。

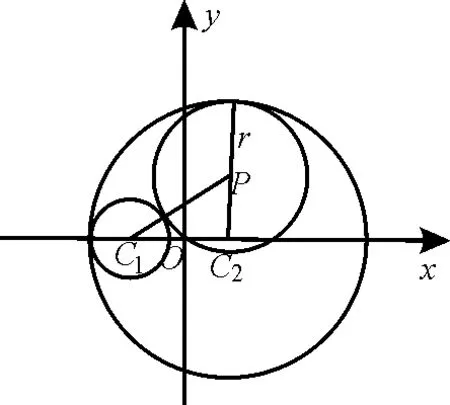
图1

如图1,由条件知两圆半径分别是13和3,设P(x,y),动圆半径 为 r。 则 有消去r得|PC1|+|PC2|=16,即P点到两定点C1、C2的距离之和是定值16,且16＞|C1C2|。所以点P的轨迹是椭圆,易求得其轨迹方程为=1。

二、求离心率

例2设椭圆(a＞b＞0)的左、右焦点分别为F1、F2,如果椭圆上存在点P,使∠F1PF2=90°,求离心率e的取值范围。

解析:先找到e与某个三角函数之间的关系,再利用已知角的范围得到这个三角函数的取值范围即可求解。

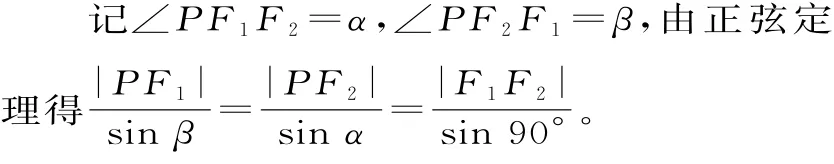
评注:找出本题的不等关系是解题的关键,椭圆的定义中隐含的不等关系主要有:

(1)设点P为椭圆C上一点,则有||PF1|-|PF2||≤2c;

(2)设点P为椭圆C上一点,则有|PF1|+|PF2|≥2c。

三、求最值

例3如图2,点A(4,0),B(2,2)在椭圆内,点M是椭圆上的动点,求|MA|+|MB|的最值。

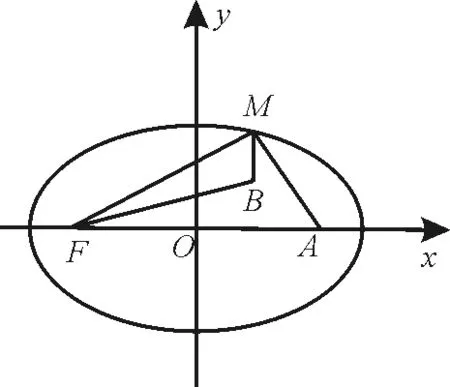
图2

解析:易知A为椭圆的右焦点,则|MA|是一条焦半径,故考虑用椭圆定义解题。

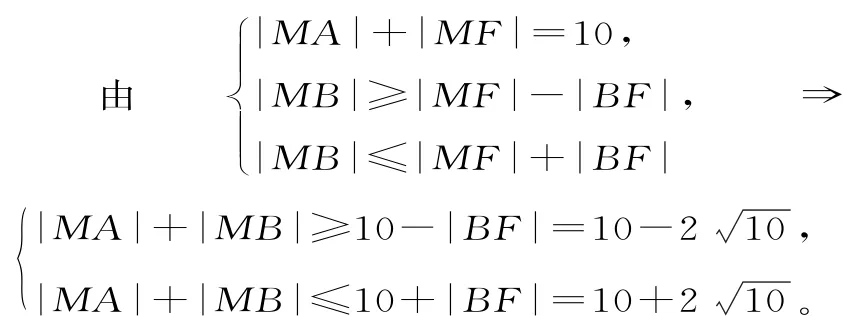
解得|MA|+|MB|的最大值为10+2,最小值为10-2。