常用逻辑用语要点导学

■郑州工业应用技术学院

一、知识盘点

1.命题

在数学中,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫作命题。其中判断为真的语句叫作真命题,判断为假的语句叫作假命题。

2.四种命题及其关系

(1)四种命题间的相互关系(如图1)。

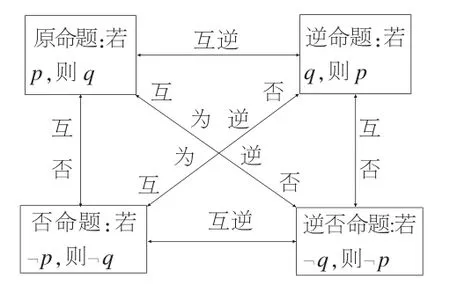
图1

(2)四种命题的真假关系:①两个命题互为逆否命题,它们有相同的真假性;②两个命题为互逆命题或互否命题,它们的真假性没有关系。

3.充分条件与必要条件

(1)如果p⇒q,则p是q的充分条件,q是p的必要条件。

(2)如果p⇒q,q⇒p,则p是q的充分必要条件,记作p⇔q。

4.命题p∧q、p∨q,￢p的真假判定

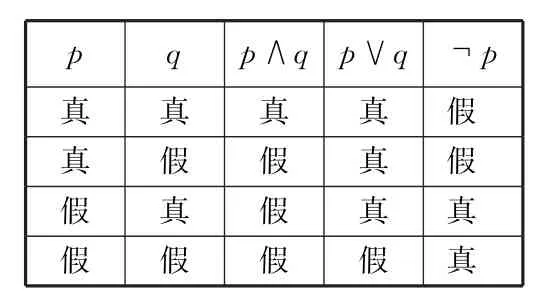
表1

5.全称量词和存在量词

(1)全称量词有:所有的,任意一个,任给,用符号“∀”表示;存在量词有:存在一个,至少有一个,有些,用符号“∃”表示。

(2)含有全称量词的命题,叫作全称命题。“对M中任意一个x,有p(x)成立”用符号简记为:∀x∈M,p(x)。

(3)含有存在量词的命题,叫作特称命题。“存在M中元素x0,使p(x0)成立”用符号简记为:∃x0∈M,p(x0)。

6.含有一个量词的命题的否定

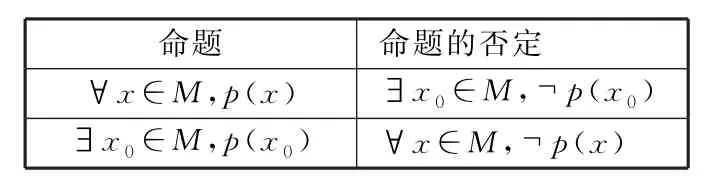
表2

二、方法小结

1.判断四种命题间的关系的方法

(1)在判断四种命题之间的关系时,首先要注意分清命题的条件与结论,再比较每个命题的条件与结论之间的关系。要注意四种命题关系的相对性,一旦一个命题定为原命题,也就相应地有了它的“逆命题”“否命题”“逆否命题”。

(2)当一个命题有大前提而要写出其他三种命题时,必须保留大前提,也就是大前提不动。

2.判断充要条件的方法

(1)命题判断法:设“若p,则q”为原命题,原命题为真,逆命题为假时,则p是q的充分不必要条件;原命题为假,逆命题为真时,p是q的必要不充分条件;原命题与逆命题都为真时,p是q的充要条件;原命题与逆命题都为假时,p是q的既不充分也不必要条件。

(2)集合判断法:从集合的观点,建立命题p,q相应的集合,p:A={x|p(x)成立},q:B={x|q(x)成立},那么若A是B的真子集,则p是q的充分不必要条件,q是p的必要不充分条件;若A=B,则p是q的充要条件;若A不是B的子集且B也不是A的子集,则p是q的既不充分也不必要条件。

(3)等价转化法:p是q的什么条件等价于￢q是￢p的什么条件。

3.全称命题真假的判断方法

(1)要判断一个全称命题是真命题,必须对限定的集合M中的每一个元素x,证明p(x)成立。

(2)要判断一个全称命题是假命题,只需例举出集合M中的一个特殊值x=x0,使p(x0)不成立即可。

4.特称命题真假的判断方法

要判断一个特称命题是真命题,只要在限定的集合M中,找到一个x=x0,使p(x0)成立即可,否则这一特称命题就是假命题。

5.对含有一个量词的命题进行否定的方法

一般地,写含有一个量词的命题的否定,首先要明确这个命题是全称命题还是特称命题,并找到其量词的位置及相应结论,然后把命题中的全称量词改成存在量词或存在量词改成全称量词,同时否定结论。

三、特别提醒

(1)否命题与命题的否定是不相同的,若p表示命题,“非p”叫作命题的否定。如果原命题是“若p,则q”,否命题是“若￢p,则￢q”,而命题的否定是“若p,则￢q”,即只否定结论。

(2)当一个命题的真假不易判断时,往往可以判断原命题的逆否命题的真假,从而得出原命题的真假。

(3)对于省略量词的命题,应先挖掘命题中隐含的量词,改写成含量词的完整形式,再写出命题的否定。

(4)命题p或q的否定为:￢p且￢q;命题p且q的否定为:￢p或￢q。

(5)由于全称命题的否定变为特称命题,因此,可以通过“举反例”来否定一个全称命题。

四、基本题型

题型一 四种命题及其真假判断

本题型考查简单命题的真假判断和命题的四种形式,多以原命题的否命题、逆否命题的形式出现。

例1(2018·南昌十校模拟)命题:已知a,b,c为实数,若abc=0,则a,b,c中至少有一个等于0。在该命题的逆命题、否命题、逆否命题中,真命题的个数为( )。

A.0 B.1 C.2 D.3

解析:原命题为真命题,其逆命题为“已知a,b,c为实数,若a,b,c中至少有一个等于0,则abc=0”,也为真命题。根据命题的等价关系可知其否命题、逆否命题也是真命题,故在该命题的逆命题、否命题、逆否命题中,真命题的个数为3。故答案为D。

解题秘籍:(1)由原命题写出其他三种命题,关键要分清原命题的条件和结论,将条件与结论互换即得逆命题,将条件与结论同时否定即得否命题,将条件与结论互换的同时进行否定即得逆否命题。(2)命题真假的判断方法:①联系已有的数学公式、定理、结论进行直接判断;②利用原命题和其逆否命题的等价关系进行判断。

题型二 充分条件、必要条件的判断

本题型主要以其他知识为背景,考查充要条件的判断,多与函数的性质、不等式的性质及其应用,解析几何中的直线与圆,圆锥曲线的位置关系以及空间中的线面位置关系等知识交汇。

例2(1)(2018·衡阳联考)设p:x2-x-20＞0,q:log2(x-5)＜2,则p是q的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

(2)(2018·惠州市调研)设函数y=f(x),x∈R,“y=|f(x)|是偶函数”是“y=f(x)的图像关于原点对称”的( )。

A.充分不必要条件

B.充要条件

C.必要不充分条件

D.既不充分也不必要条件

解析:(1)因为x2-x-20＞0,所以x＞5或x＜-4,p:x＞5或x＜-4。

因为log2(x-5)＜2,所以0＜x-5＜4,即5＜x＜9,q:5＜x＜9。

因为{x|5＜x＜9}⊂{x|x＞5或x＜-4},所以p是q的必要不充分条件。故选B。

(2)设f(x)=x2,y=|f(x)|是偶函数,但是不能推出y=f(x)的图像关于原点对称。

反之,若y=f(x)的图像关于原点对称,则y=f(x)是奇函数,这时y=|f(x)|是偶函数。故选C。

解题秘籍:充分条件、必要条件的判定方法有定义法、集合法和等价转化法。三种不同的方法适用于不同的类型,定义法适用于定义、定理判断型问题;而集合法多适用于命题中涉及字母范围的推断问题;等价转化法适用于条件和结论带有否定性词语的命题,常转化为其逆否命题来判断。

题型三 充要条件的应用

例3(2018·济南月考)已知P={x|x2-8x-20≤0},S={x|1-m≤x≤1+m},是否存在实数m,使得x∈P是x∈S的充分必要条件?若存在,请求出m的取值范围。

解析:解得P={x|x2-8x-20≤0}={x|-2≤x≤10}。

要使x∈P是x∈S的充分必要条件,则P=S,{x|-2≤x≤10}={x|1-m≤x≤1+m}。

因此,不存在实数m,使得x∈P是x∈S的充分必要条件。

解题秘籍:解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式求解。

题型四 含有逻辑联结词的命题的真假判断

解析:对于命题p,当x=4时,x+00,故命题p为真命题。对于命题q,当x=4时,24=42=16,即∃x0∈(2,+∞),使得成立,故命题q为假命题。所以p∧(￢q)为真命题,故选A。

解题秘籍:若要判断一个含有逻辑联结词的命题的真假,其步骤如下:(1)判断复合命题的结构;(2)判断构成这个命题的每个简单命题的真假;(3)依据含有“或”、“且”、“非”的命题的真假判断方法,进行判断即可。

题型五 写出全称命题或特称命题的否定

给出一个与不等式有关的全称命题或特称命题,要求直接写出它的否定。

例5(1)(2018·郑州模拟)命题“∃x0∈R,x20-x0-1＞0”的否定是( )。

A.∀x∈R,x2-x-1≤0

B.∀x∈R,x2-x-1＞0

C.∃x0∈R,x20-x0-1≤0

D.∃x0∈R,x20-x0-1≥0

解析:(1)依题意得,命题“∃x0∈R,x20-x0-1＞0”的否定是“∀x∈R,x2-x-1≤0”,故选A。

解题秘籍:全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词,存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论即可。同时需注意,对于省略量词的命题,应先挖掘命题中隐含的量词,改写成含量词的完整形式,再写出命题的否定。