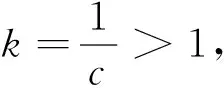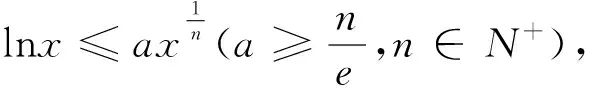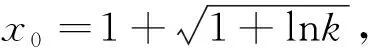探析含参函数零点两侧附近函数值符号的解题策略

福建省泉州市第七中学 (362000)

郭富梅 林志斌

近几年来，全国高考卷的压轴题常常是函数零点问题，由函数零点定理知，要判断函数零点的存在，需要寻找两个端点并判断这两端点的函数值异号，当碰到含参函数零点不可求，且无法直接判断零点两侧附近的函数值符号时，学生只能走江湖，大约通过图像猜想零点个数，解答过程不够严谨，很多高考题的解答过程也是犹如天降，直接给出答案，并没有给出常规的解法，学生老师很多时候也摸不着头脑，下面结合这几年的教学经验，结合实例，初步探析解决含参函数零点两侧附近符号的几种解题策略，供大家参考．

1.赋值法

对于函数的特征比较明显，通过观察，在所要判断的区间内具体赋值，并判断函数值的符号．

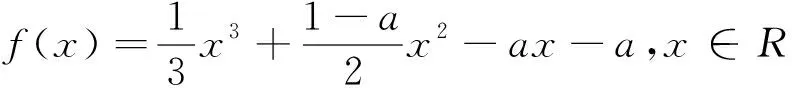
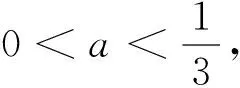
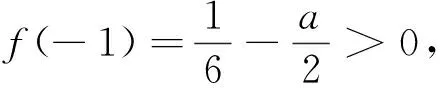
2.重新合并同类项法

对于有些函数不易观察出函数零点两侧附近的函数值符号，可通过对函数重新分解、重新合并同类项，寻找函数大于零或小于零的充分条件．

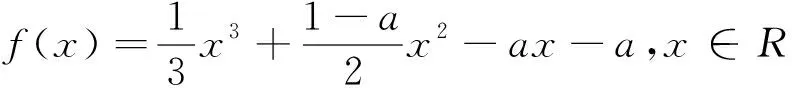
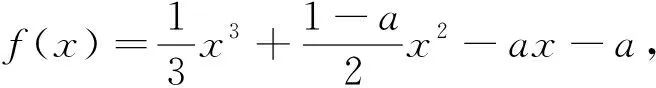
例3 (2016全国卷改编)已知函数f(x)=(x-2)ex+a(x-1)2,其中a>0，求证；f(x)有两个零点．

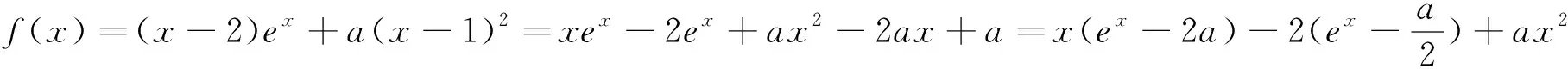
3.执果索因法

根据函数的具体特征，寻找满足函数大于零或小于零的充分条件.

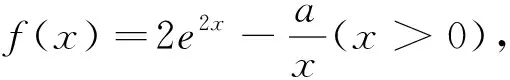
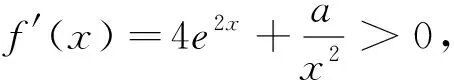
下面探析在(0，a)存在一点x0使f(x0)<0．

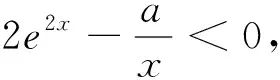
4.放缩法

对于有些函数不易观察出函数零点两侧附近的函数值符号，可通过适当缩小范围，适当放缩，以达到能解出或找出函数大于零或小于零的充分条件．

例3中的探析在(-∞，1)存在一点x0使f(x0)>0，也可以采用适当放缩法，以达到能找出函数小于零的点或范围．

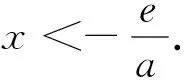
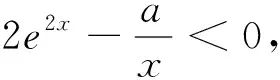
在对于含有指数函数与对数函数的函数式，经常利用常见不等式进行放缩，达到能够找出函数大于零或小于零的充分条件．

常见的几个放大的不等式：

常见的几个缩小的不等式：

上述不等式还可根据题目的需要对参数a与n取不同值，避免放缩过大或过小．

例5 (2017全国卷改编)已知函数f(x)=ae2x+(a-2)ex-x.a∈(0,1)，求证：f(x)有两个零点.

解：f(x)的定义域为(-∞,+∞)，f′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1)，其中a∈(0,1)，由f′(x)<0解得x∈(-∞,-lna)；f′(x)>0解得x∈(-lna,+∞)，所以f(x)在

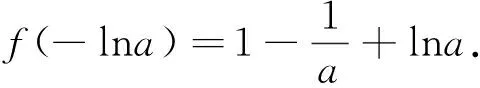
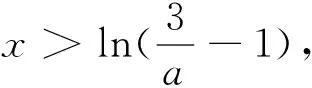
例6 (2014福建高考卷改编)求证：对任意给定的0