基于锥模型的一种新非单调信赖域算法
邢治业
(山西工程职业技术学院 基础部,山西 太原030009)
1.引言
本文考虑以下非线性无约束优化问题
(1)
其中f(x)为二次连续可微函数且有下界,解决上述问题一般采用信赖域方法[1-4],一般构造子问题模型如下:
(2)
这里,Sk为子问题的解,gk=f(xk)是当前点xk的梯度,bk和Bk分别为n维向量和n×n阶正定对称矩阵,△k是信赖域半径。
当bk=0时,上述锥模型就转化为二次模型。锥模型[5-8]有较多的自由度,可以更好的逼近目标函数,并且具有丰富的迭代点信息,提高算法的有效率。
近年来,许多学者将非单调技术加入到信赖域算法中[9-11],算法取得了良好的计算效果,而且加快了收敛速度。尽管传统的非单调技术有众多优点,但也存在丢失最优迭代点等缺点,基于上述问题,本文在前人研究[12~13]的基础上,结合新非单调技术、wolfe线搜索,应用于锥模型信赖域算法,提出有效且收敛效果较好的新非单调锥模型信赖域算法。
2.算法的提出
本节中,所采用的新非单调技术形式为:
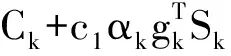

(3)
(4)
ηk-1∈[ηmin,ηmax],0≤ηmin≤ηmax<1

现在将新算法描述如下:
Step0:置初始点xk∈Rn,b0∈Rn,B0∈Rn×n为对称矩阵,△>0,ε≥0,τ>0,
C1=f(x1),Q1=1,0≤ηmin≤ηmax<1,k:=0.
Step1:计算gk,若‖gk‖≤ε,则停止。
Step2:否则解锥模型子问题式(2)得sk.
Step4:如果rk≥u,xk+1=xk+Sk,△k+1∈[‖Sk‖,r3‖Sk‖];否则求αk满足Wolfe线搜索

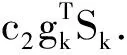

3.新算法的收敛性
为证算法的收敛性,我们作以下假设:
(A1)水平集S={x∈Rn∶f(x)≤f(x0)}有界,其中x0为初始点。
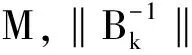
引理1[9]令sk是算法(3)产生的解,则有
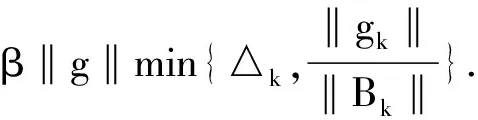
(5)
引理2 若假设(A1)(A3)成立,{xk}为上述算法产生的点列,则fk+1≤Ck+1≤Ck且数列{Ck}收敛。
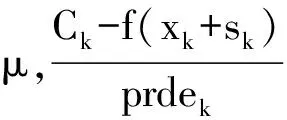

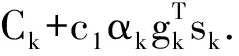
综上所述fk+1≤Ck+1≤Ck,因为S(x)是有界闭集,所以{Ck}非增且收敛.


(6)
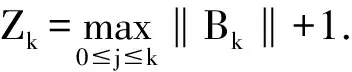

(7)

(8)
下面用数学归纳法证明此引理成立。

现假设当n=k时,引理显然成立.
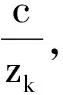
(9)
当△k+1∈[‖sk‖,c3‖sk‖]时,有△k+1≥△k,rk≥μ,容易证明结论成立。
下面只需考虑△k+1∈[c1‖sk‖,c2‖sk‖]这种情况,此时有
(10)

(11)


由式(10)和式(11)可得:

(12)

(13)

(14)
将式(14)代入式(10)结合式(11)可得出以下结论
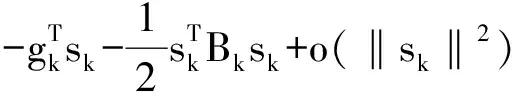
(15)
将式(15)两边乘(1-u)加到式(12)可得:

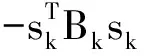
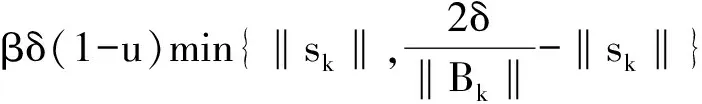
(16)

(17)
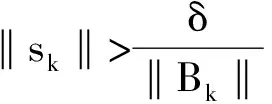
(18)
式(17)和式(18)必有一个成立,又由式(10)得