一种改进的自适应信赖域算法
胡梦英
北京邮电大学理学院
一种改进的自适应信赖域算法
胡梦英
北京邮电大学理学院
胡梦英,女,硕士在读,北京邮电大学理学院,主要研究方向为最优化算法。
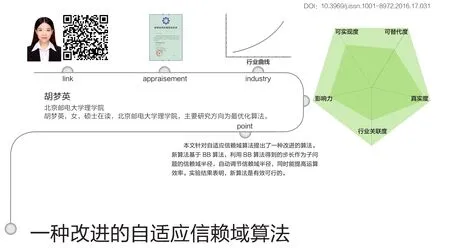
考虑无约束极小化问题

其中f:Rn→R 二次连续可微。
求解上述无约束问题主要有信赖域法和线搜索法。线性搜索先确定方向再确定步长,信赖域法则是先确定步长再确定方向。信赖域方法的主要思想是围绕当前迭代点xk定义一个区域,即信赖域,使二次模型在信赖域内能充分近似目标函数,之后求解信赖域子问题得到试探步长,然后用某一评价函数来决定是否接受该试探步长以及决定下一次迭代的信赖域。信赖域法具有很强的全局收敛性,但是算法效率会受到子问题中信赖域半径大小的影响。
对于无约束优化问题的信赖域算法,子问题中二次模型的信赖域半径大小的选择是关键。本文的改进自适应信赖域算法,利用BB算法得到的步长作为子问题的信赖域半径,随着迭代的进行自动调节信赖域半径,提高运算效率。
自适应信赖域算法
信赖域半径大小的选择是影响每一步迭代效率的关键。如果信赖域太小,则算法就可能得不到目标函数的最优点,影响迭代速度。反之如果信赖域太大,则二次模型与目标函数近似程度不高,因而不得不减少信赖域并重新计算。自适应信赖域算法中信赖域半径随每一次迭代的进行而自动改变,是对传统信赖域算法的一个改进。
自适应信赖域法的信赖域子问题:
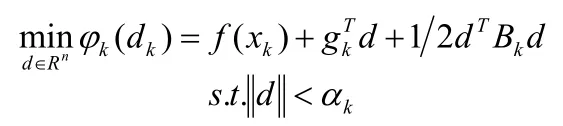
BB算法
BB算法是Barzilai和Borwein提出的Two-Point Step Size Gradient Methods。BB算法的基本思路是用当前迭代点以及前一点的信息来确定步长因子。迭代公式可以看成是
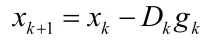
因此计算得出,
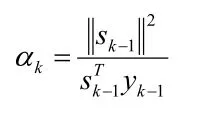
改进的自适应信赖域算法
改进思路
自适应信赖域算法中信赖域半径自动调节,本文提出的新算法利用BB算法得到的步长的倍数作为信赖域子问题的信赖域半径,这其实是一种自适应信赖域算法。
新得到的信赖域的子问题为:
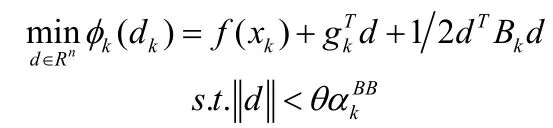
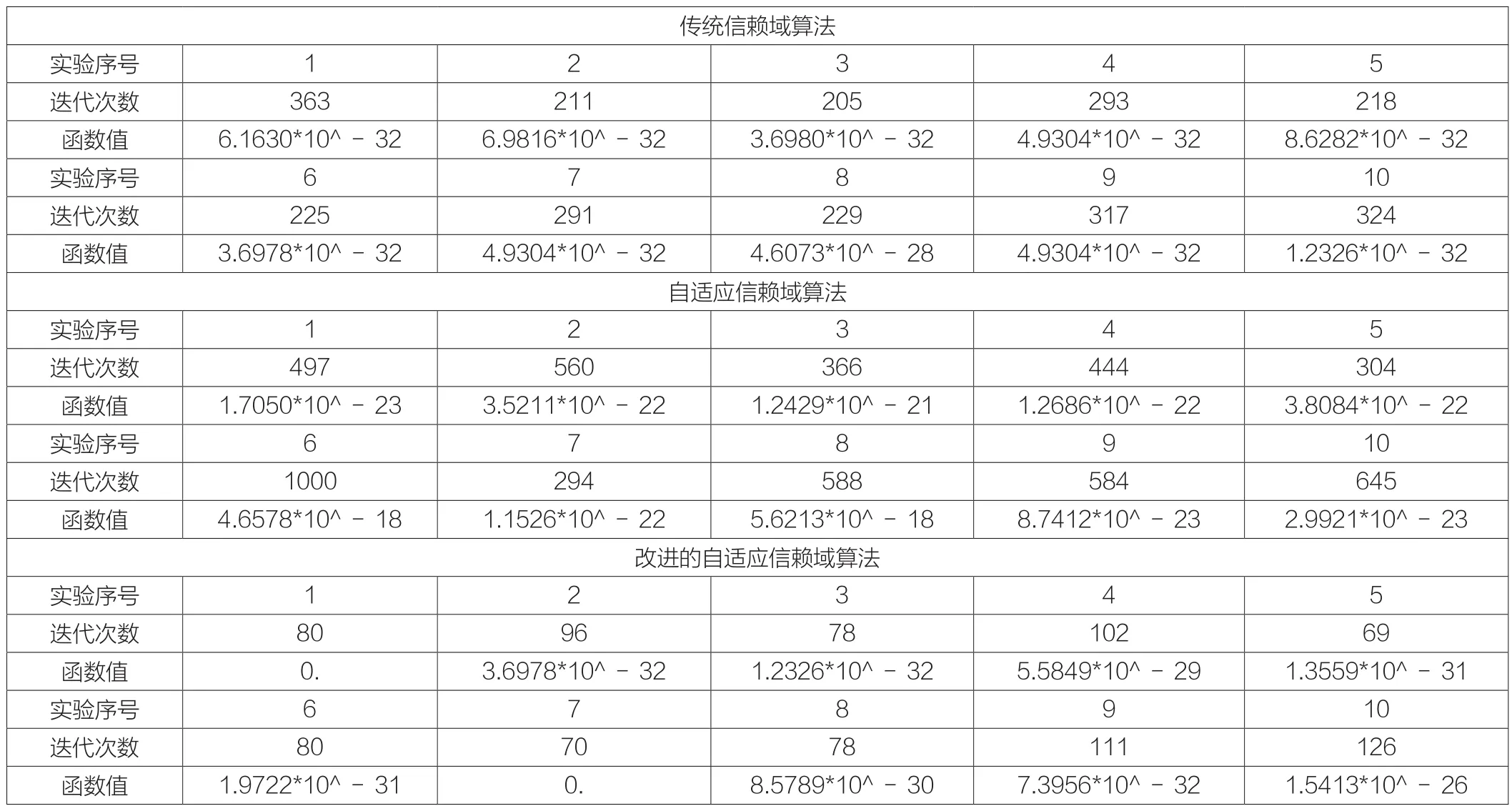
表1 三种算法的运行结果
算法步骤
Step1 给定初始点x0,初始信赖域半径α0,给定θ的值,参数0<µ<η<1,置k=1。
Step2 计算gk,若则停止,否则转Step3。
Step3 求解子问题(3.1),得到近似解dk。
Step6 令k=k+1,返回Step2。
数值实验
本次数值实验,我们选用的编程环境为Mathematics8.0。用Mathematics语言分别编写了传统信赖域算法、自适应信赖域算法和改进自适应信赖域算法的算法程序。
选用的测试函数
测试算法
1.传统信赖域算法
传统信赖域算法的信赖域子问题:
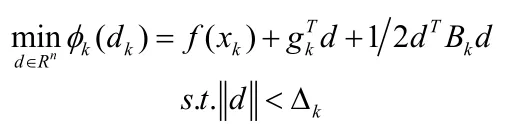
其中∆k是信赖域半径。
2.自适应信赖域算法
自适应信赖域法的信赖域子问题:
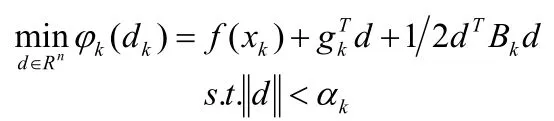
3.改进的自适应信赖域算法
改进的自适应信赖域法的信赖域子问题:
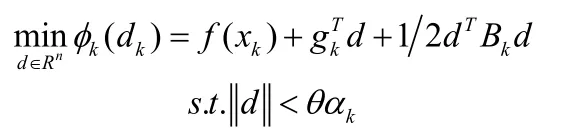
数值结果
实验一:Rosenbrock函数,
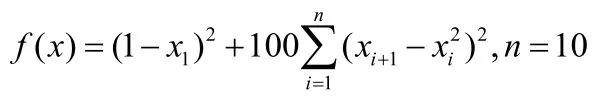
实验二:
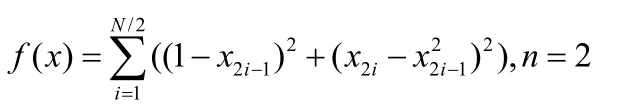
实验三:
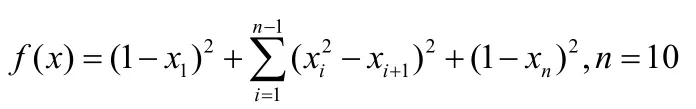
从表中结果分析:无论对于一些维数较高的测试问题,还是次数较高的函数来说,改进的自适应信赖域算法具有良好的计算效能。改进算法迭代次数少,效率高,误差小。
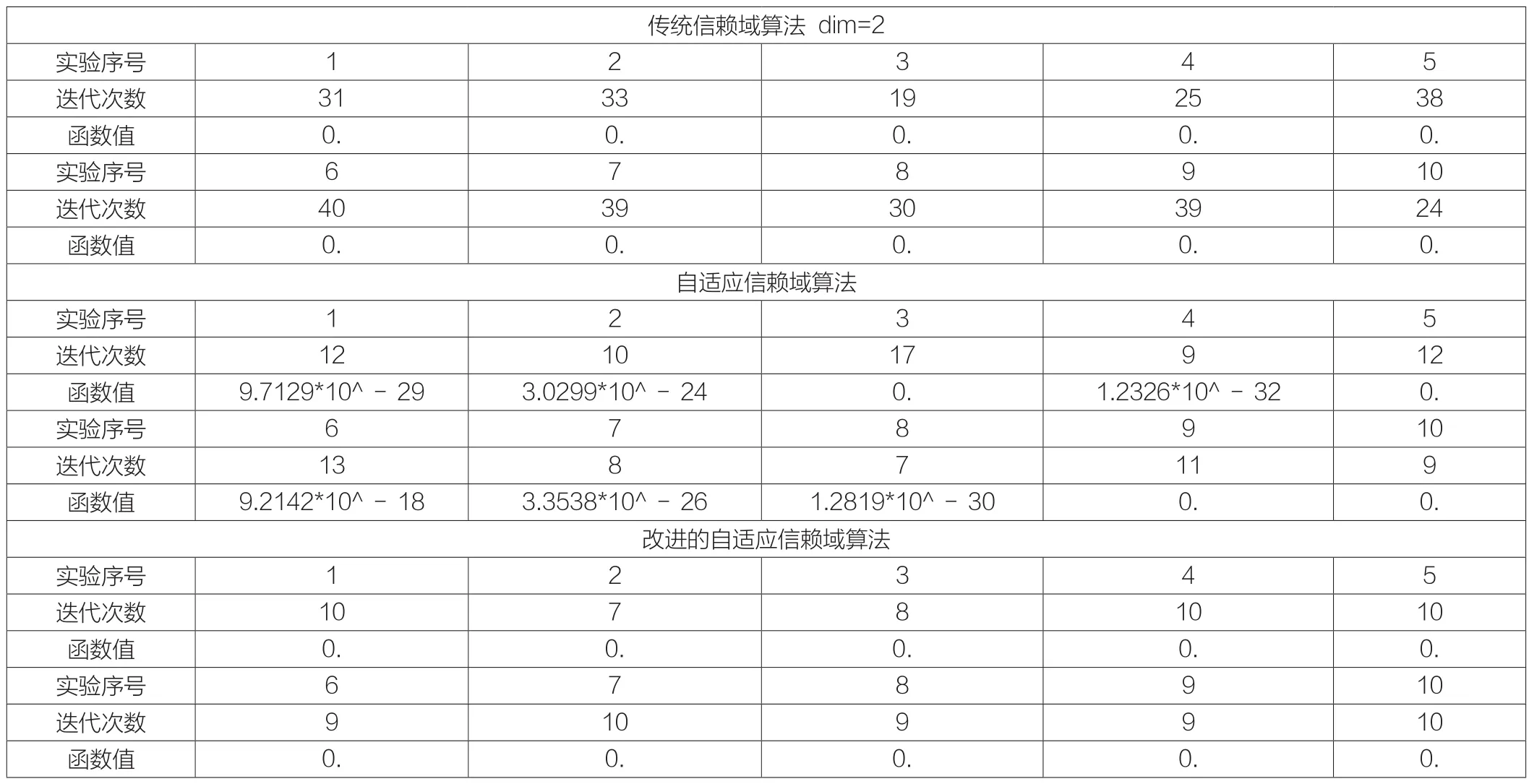
表2 三种算法的运行结果
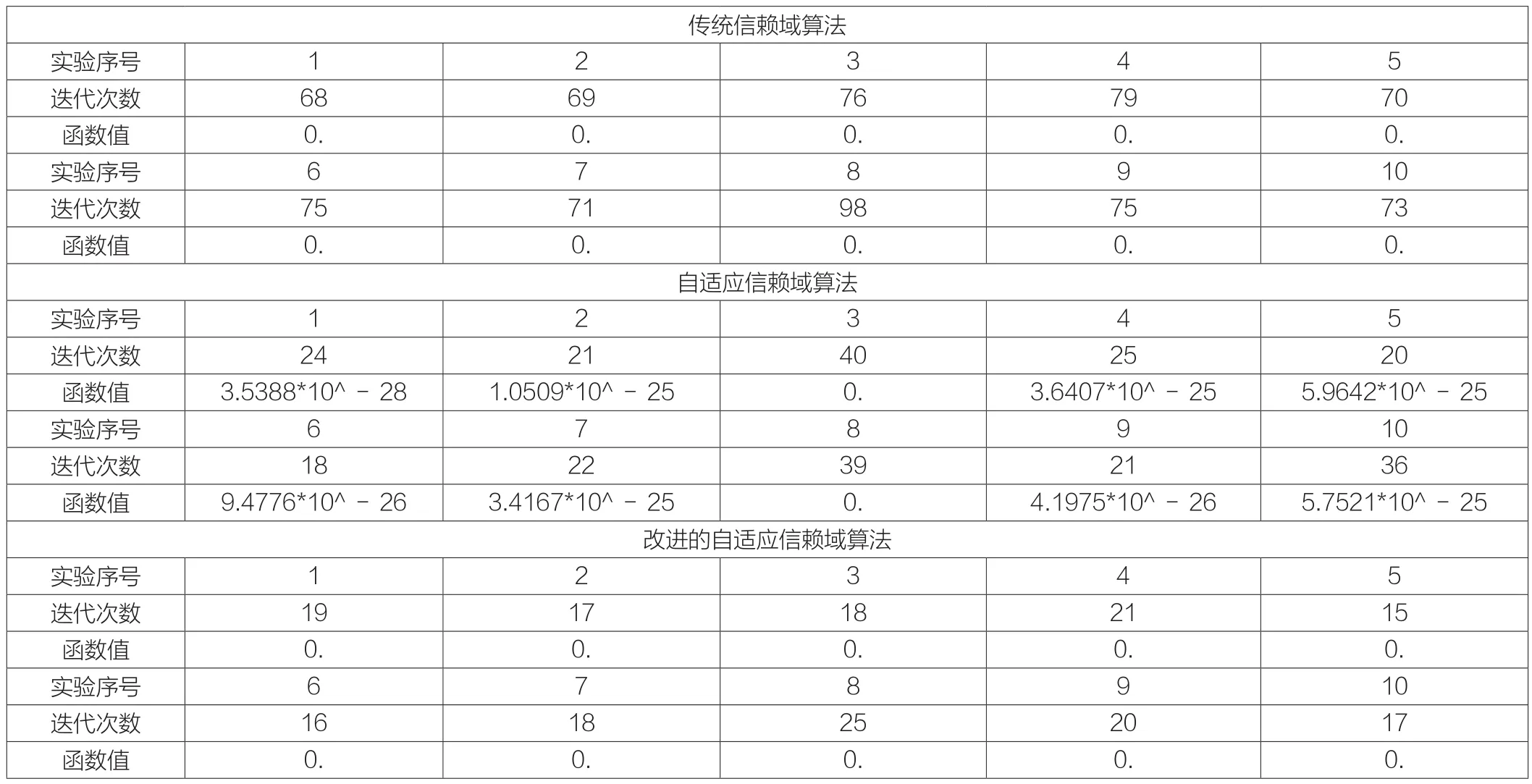
表3 三种算法的运行结果
结语
对于求解无约束优化问题最优解的信赖域算法,子问题二次模型的信赖域半径的大小的选择是影响算法收敛速度的关键。本文提出改进自适应信赖域算法,利用BB算法得到的步长作为子问题的信赖域半径,用BB步长自动调节信赖域半径。数值实验结果显示改进算法具有良好的计算效能,不管是迭代步数还是精度,本文的改进算法都有较好的计算性能。

