隧道沉降引起的轨道结构变形与脱空

杨成永，程 霖, 余 乐，韩薛果

(1.北京交通大学 土木建筑工程学院，北京 100044；2.北京城市快轨建设管理有限公司，北京 100027)

城市地铁穿越施工引起既有地铁隧道结构变形，进而引起其内的轨道结构产生变形。轨道结构的变形直接关系到地铁列车的运营安全，其变形大小决定着新建工程设计方案和施工方法的选择，也决定着既有线列车运营采取的安全保证措施。

但在目前穿越施工的结构分析中，没有考虑钢轨—道床—隧道结构间的相互作用，简单地视钢轨的沉降等同于隧道结构沉降。实际的监测结果表明：当隧道结构沉降较小时，钢轨与道床间、道床与隧道底板间的沉降差异被测量误差所掩盖；当隧道结构沉降较大时，钢轨、道床、隧道间的沉降差异就较大，明显超过测量误差(目前测量误差可控制在0.3 mm以下)，严重时轨道与道床、道床与隧道底板间还会产生脱离[1-3]。

钢轨—道床—隧道的相互作用问题具有复杂性，加之道床还有不同形式，以往一般采用数值方法进行模拟，理论分析方面的研究主要采用弹性地基梁法。根据可处理变形大小的不同，理论分析方法又分为小变形问题的弹性地基梁模型[4-6]和大变形问题的弹性地基梁模型[7-8]。

本文针对盾构隧道中的支承块式道床轨道结构，采用弹性地基梁模型和傅里叶三角级数解法，分析钢轨—支承块—道床—隧道间的共同变形问题。在提出轨道(这里指钢轨或者钢轨与道床组成的叠合梁)变形的简化假设后，直接从微元体的平衡出发，建立了控制微分方程。假设隧道沉降符合正态曲线，并引入阶梯函数描述轨道与基底脱空段及接触段的地基抗力，推导了求解轨道沉降的傅里叶系数的线性方程组。采用北京地铁支承块式轨道参数计算了沉降大小、沉降槽宽度、脱开方式等因素对轨道变形和内力的影响。

1 控制微分方程

把轨道视为一维杆件，并采用下列假设。

(1) 轨道变形满足平截面假设，即垂直于轨道轴线的横截面变形后仍为平面且垂直于轴线。

(2) 基底对轨道的作用力垂直于轨道轴线。

(3) 轨道刚度保持不变。

(4) 轨道的轴向变形和轴力只发生在沉降槽附近一定范围内并且是一常量。

图1为轨道微元的受力图。图中：N为轨道轴力，N；Q为轨道剪力，N；M为轨道弯矩，N·m；q为轨道荷载，N或N·m-1，向上为正；w(x)为轨道竖向位移，m，向上为正；x为沿轨道轴线的坐标(基底沉降槽中点处x=0)，m。

图1 轨道微元的受力

由轨道微元的受力可得轨道变形的平衡方程为

(1)

式中：ζ为轨道的一维度规(轨道变形后长度与变形前长度的比值)。

引用Love-Kirchhoff假设，有弯矩M与挠度w(x)的关系

(2)

式中：E为轨道弹性模量，Pa；I为轨道横截面的惯性矩，m4。

将式(2)代入式(1)中第1式得

(3)

采用前述假设(4)，式(1)中的第2式被舍去。然后把式(3)代入式(1)中第3式得轨道变形的控制微分方程为[8]

(4)

假定轨道的沉降变形符合正态曲线，则轨道一维度规和轴力的表达式分别为[8]

(5)

(6)

式中：w0为轨道在沉降槽中点处(x=0)的最大沉降，m；j为轨道沉降槽半宽，即沉降曲线反弯点距x=0处的水平距离，m；A为轨道的横截面积，m2；L为轨道计算范围的半宽，m。

2 轨道荷载及边界条件

置于基底(隧道底板)上的轨道，在轨道与基底保持接触区段，受其自重和Winkler地基反力作用；在轨道与基底脱空区段，只受自重作用。式(4)中右端的轨道荷载q可表示为

(7)

式中：γ为轨道的线密度，kg·m-1；g为重力加速度，m·s-2；K为地基系数，Pa·m-1；b为轨道宽度，m；S(x)为基底沉降，m；c为轨道与基底在沉降槽中部脱开范围的半宽，m。

假定基底沉降遵从正态曲线，即

(8)

式中：S0为基底在沉降槽中点处(x=0)的最大沉降，m；i为基底沉降槽半宽，即沉降曲线反弯点距x=0处的水平距离，m。

对于无缝线路，轨道长度可以视为无限长。在不考虑道床板沉降缝影响条件下，轨道的两端在沉降槽以外，其边界条件视为固支；由于对称，中间点(x=0处)的转角为0，则有

(9)

3 控制方程的傅里叶级数解法

由于要考虑轨道与基底的脱空，需要用到Heaviside阶梯函数，即

(10)

把式(7)代入式(4)，并引入阶梯函数得到

gγ=0

(11)

进行傅里叶级数求解，需要把式(11)中的w(x)，S(x)及H(x)均展开成三角级数。由于w(x)，S(x)及H(x)均为偶函数，均可在[-L, +L]上展成余弦级数。

轨道沉降w(x)在[-L, +L]上的傅里叶级数展开为

(12)

式中：a0和ak为待求的傅里叶级数的系数。

应注意到，式(12)已满足边界条件式(9) (中点和两端点转角为0)。

由式(12)，得轨道沉降的各阶导数为

(13)

(14)

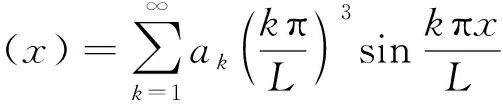
(15)

(16)

基底沉降S(x)在[-L, +L]上的级数展开为

(17)

其中，

式中：b0和bk为级数的系数。

当L取3i以上时，则[9]

(18)

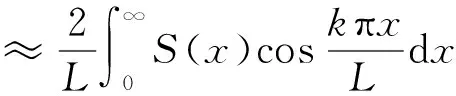
(19)

阶梯函数H(x)在[-L, +L]上的级数展开为

(20)

其中，

式中：H0和Hk为级数的系数。

为将式(11)中第3项表示成级数，需要计算阶梯函数H(x)与轨道沉降w(x)及基底沉降S(x)的乘积。

w(x)与H(x)相乘的傅里叶级数为

(21)

根据傅里叶级数相乘的法则[10]，则

(22)

(23)

S(x)与H(x)相乘为

(24)

其中，

将式(14)、式(16)、式(21)和式(24)代入微分方程(11)式后得到

(25)

式 (25)为无穷线性代数方程组。把式(22)的α0、式(23)的αk代入式(25)，且只取前n项有

(26)

式(26)即为确定式(12)中待定系数a0和ak的线性代数方程组。式(26)有n+1个方程，n+4个未知量：a0至an，c(含在Hk(k=0～2n)中)以及度规ζ和轴力N。根据式(5)和式(6)，式(26)中未知量度规ζ和轴力N可用另外2个未知量轨道沉降槽参数w0和j来表示。

下面分3种情况讨论3个多余未知量的确定方法。

(1) 考虑轨道的伸长，但不考虑轨道与基底的脱空。仅考虑伸长时，由于无脱空，有c=0。式(26)中有a0至an及ζ和N共计n+3个未知数，多出2个未知数ζ和N。采用迭代方法确定如下：

第1次按无伸长计算，取ζ=1,N=0，求解线性方程组得到待定系数a0和ak。然后根据得到的挠曲线找出w0(1)和j(1)。第2次按照w0(1)和j(1)进行伸长计算得到w0(2)和j(2)。以此类推直到2次计算的w0和j相差足够小为止。

(2) 不考虑轨道的伸长，但考虑轨道与基底的脱空。仅考虑脱空时，由于无伸长，有ζ=1，N=0。式(26)中有a0至an及c共计n+2个未知数，多出1个未知数即脱空范围c。同样采用迭代方法确定如下：

第1次求解时首先假设全长接触无脱空，即c=0。根据计算得到挠曲线w(x)， 判定是否有脱离区域(w(x)≤S(x))。如果没有，那么该解即为所求之解。如果有，则从中点往两侧寻求脱离点w(x) =S(x)的坐标x(1)， 该坐标即为c的第一近似值。 令c=x(1)进行第2次求解， 得到x(2)。 以此类推直到x(k)和x(k-1)相差足够小为止。 最后一轮计算得到的x(k)=c及w(x)，即为该问题的三角级数解。

(3) 同时考虑轨道的伸长及轨道与基底的脱空。同时考虑脱空与伸长，可以按前述办法先迭代脱空，再迭代伸长。在实践中，同时考虑两者的意义不大。因为当轨道与基底产生脱离后，轨道的沉降将显著减小，伸长量也将大为减小。因此，此时考虑伸长对轨道的变形和内力影响不大。

4 实例计算

采用北京地铁某工点支承块式道床的数据：60钢轨，钢轨底面宽度15 cm，高度17.6 cm，截面面积77.45 cm2，弹性模量210 GPa ，惯性矩3 217 cm4(换算钢轨宽度7.081 cm)，每延米质量60.643 kg(对应每个支承块的钢轨质量36.097 kg)。钢轨支座1680个·km-1，支承块质量109.76 kg·个-1，支承块下橡胶垫板竖向刚度80 kN·mm-1，扣件竖向刚度40 kN·mm-1(橡胶垫板与扣件串联的竖向刚度26.667 kN·mm-1)。道床板为C30钢筋混凝土，宽度3.3 m，厚度0.3 m，弹性模量30 GPa，惯性矩742 500 cm4，密度2 420 kg/m3，每延米质量2 395.8 kg。

现场监测结果为：右线隧道底板沉降槽半宽4.8 m，最大沉降10.19 mm，道床最大沉降10.14 mm；左线隧道底板沉降槽半宽4.1 m，最大沉降25.78 mm，道床最大沉降24.83 mm。

用C语言编程，式(26)的求解采用克劳特(Crout)分解[11]。对实例数据及下列影响轨道结构变形和脱空的因素进行计算。

(1) 钢轨的轴力和伸长的影响。隧道最大沉降值取48 mm，沉降槽半宽取2 m。

(2) 隧道底板最大沉降值的影响。沉降槽半宽取3 m，最大沉降值分别为3，6 ，12，24 和48 mm。

(3) 隧道底板沉降槽宽度的影响。最大沉降值取48 mm，沉降槽半宽分别为2，3，4和5 m。

(4) 钢轨与道床及隧道底板间脱空方式的影响。参见图2，分3种情况：①是钢轨与支承块间脱离；②钢轨及支承块一起与道床脱离；③钢轨及道床一起与隧道底板脱离。钢轨悬吊起支承块时，扣件伸长量为109.76×9.81/40 000 =0.026 9 mm。

图2 支承块式道床剖面示意图

计算结果列于表1。

由表1可以得出如下结论：

(1) 对比工况1和工况2可以看出，钢轨在沉降槽半宽为2 m，沉降48 mm时仍属于小变形，考虑轴力与不考虑轴力计算结果基本相等。地铁运营部门允许既有线路的沉降一般均较小，因此，在沉降不大时，无需考虑轴力对计算结果的影响。

(2) 从工况3到工况7、工况11到工况15及工况19到工况23可以看出，在隧道沉降槽宽度一定时，钢轨及道床的沉降、沉降槽宽度、脱空范围(如果产生的话)及内力均随隧道沉降量的增加而增大。

(3) 从工况7到工况10、工况15到工况18及工况23到工况26可以看出，在考虑脱空的情况下，随隧道沉降槽宽度增大，钢轨及道床的沉降及沉降槽宽度也随之增大。由于考虑了脱空，隧道沉降槽宽度对内力的影响较为复杂。总体来说，在产生脱空时，随隧道沉降槽宽度的增大，钢轨及道床的弯矩和剪力也增大；在隧道沉降槽宽度继续增大脱空消失后，钢轨及道床的弯矩和剪力将随隧道沉降槽宽度的增大而减小。

(4) 工况3到工况10计算的是扣件失效时钢轨与支承块间的脱空。这种情况一般不会发生，但可作为钢轨沉降的限值(最小值)使用。可以看出，如果没有扣件的约束，道床在很小的沉降时，钢轨就与支承块脱开了。

表1 计算结果

注：带*的数据为现场测量值。

(5) 工况11到工况18计算的是钢轨悬吊支承块，导致支承块与道床脱离。可以看出，由于支承块重力作用，只有在道床沉降大且沉降槽宽度小的情况下，才能产生脱空。工况11到工况18的计算结果，还没有考虑支承块与道床间可能存在的摩擦力。因此，实际情形中，支承块与道床脱空更难于产生。从本次计算结果判断，沉降槽半宽3 m且道床沉降50 mm可作为支承块与道床脱空产生的条件。

(6) 工况19到工况26计算的是钢轨与道床组成叠合梁，一起与隧道底板脱离。可以看出，由于道床重力作用，只有在隧道沉降较大且沉降槽宽度小的情况下，才能产生脱空。工况19到工况26的计算结果，没有考虑道床与隧道底板间可能存在的粘结力。从本次计算结果判断，沉降槽半宽3 m且隧道底板沉降12 mm可作为道床与隧道底板脱空产生的条件。

(7) 关于钢轨与道床的沉降差，根据工况3到工况18的计算结果，可以做如下判断：在扣件正常连接条件下，道床沉降槽半宽3 m沉降值达到30 mm时，钢轨与道床间将产生沉降差；在扣件失效情况下，道床沉降槽半宽3 m沉降值达到4 mm时，钢轨与道床间将产生沉降差。对于道床与隧道底板间的沉降差，根据工况19到工况26的计算结果，可以认为：隧道底板沉降槽半宽3 m沉降值达到12 mm时，道床与隧道底板间将产生沉降差。

(8) 基底沉降槽宽度越小，沉降差出现就会越早，脱空产生也会越早。

(9) 工况27和28是对实例数据的计算，计算结果与实测数据基本一致。

5 结 论

(1)根据沉降变形的大小和钢轨—支承块—道床—隧道底板间连接状况的不同，沉降差和脱空可在钢轨与支承块间、支承块与道床之间以及道床与隧道底板间发生。

(2)总体上说，沉降槽宽度越小、沉降值越大，钢轨—支承块—道床—隧道底板间的沉降差和脱空范围也越大。

(3)在扣件失效条件下，钢轨与支承块间很容易产生沉降差和脱空。在隧道底板沉降槽半宽3 m、沉降值只有4 mm时，钢轨与道床间即产生了沉降差和脱空。

(4)在扣件正常发挥作用条件下，在隧道底板沉降槽半宽3 m、沉降值12 mm时道床与隧道底板间将产生沉降差和脱空。若沉降值继续增大，当道床沉降值达到30 mm时，钢轨与道床间将产生显著的沉降差；当道床沉降值达到50 mm时，若支承块与道床间的摩擦力不足，则支承块与道床间将产生脱离。

(5)本文未考虑道床板沉降缝的存在，沉降缝对钢轨及道床的变形、脱空及内力会产生影响，有待进一步研究。