PBL剪力键的弹性静力解析解
司秀勇,刘丽芳,肖 林
(1.燕山大学 建筑工程与力学学院,河北 秦皇岛 066004; 2.西南交通大学 土木工程学院, 四川 成都 610031)
由于PBL剪力键具有良好的刚度、延性以及疲劳性能,近年来PBL剪力键在钢混组合结构,尤其是桥梁钢混结合段中的应用越来越广泛[1-3]。
目前,国内外学者对PBL剪力键的承载能力的研究,主要集中于其静力性能如强度与刚度[4],研究方法多以试验尤其是推出试验为主[5-6]。也有一些学者采用有限元方法进行分析[7-8],但由于PBL剪力键在传力过程中的高度非线性行为,理论分析的难度较大,相关研究较少。
本文基于Airy应力函数和Winkler弹性地基梁理论,进行钢混组合结构中PBL剪力键在工作状态下的弹性静力解析解研究。
1 力学模型的建立
图1为钢—混结合段中PBL剪力键推出试验的结构简图。
在加载初期,贯穿钢筋基本不参与工作,主要是由混凝土榫提供抗力;PBL剪力键加载中期和加载后期的抗力则主要由贯穿钢筋提供,此时混凝土榫剪切失效,退化为只传递压力的混凝土圆环[9]。由于钢板的厚度远小于混凝土板的厚度。钢板及钢板内PBL剪力键部分在该方向上的位移受到混凝土巨大刚度的限制,可以将其简化为一个平面应变问题,如图2所示;钢板平面外埋置于混凝土之内的贯穿钢筋,可以用弹性支撑于混凝土中的Winkler地基梁模拟,如图3所示。

图1 PBL剪力键的一般构造

图2 混凝土圆环平面图
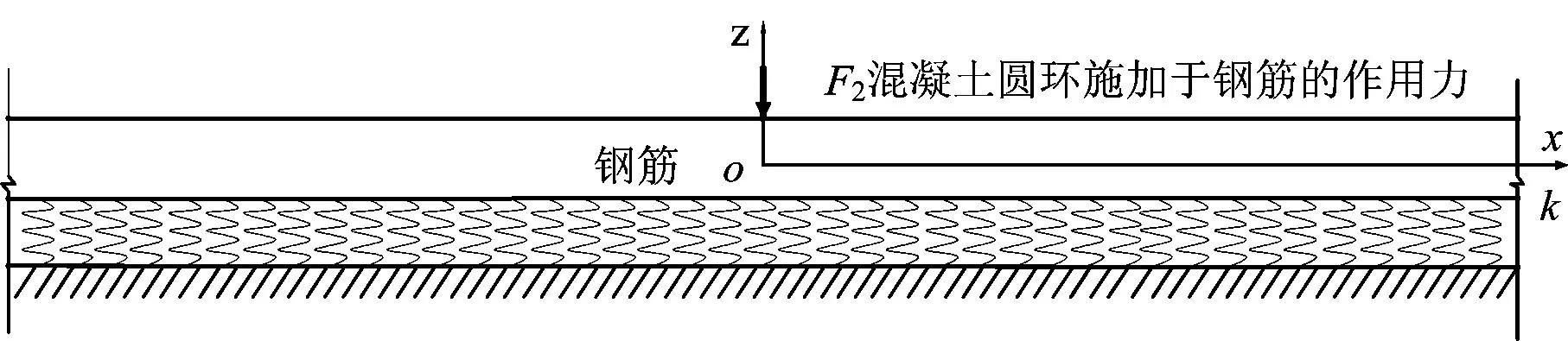
图3 贯穿钢筋的Winkler地基梁模型
2 混凝土圆环力学分析
位于钢板平面之内PBL剪力键,可以将混凝土榫的受力等效为平面应变状态的厚壁圆环,环的内外壁承受关于x轴的对称分布荷载。
该问题的解析解可借助于采用极坐标表示的Airy应力函数的一般形式得到。
2.1 基本方程的建立
建立如图4所示的混凝土圆环的力学模型,坐标原点O取在圆环中心,建立r和θ为坐标的极坐标系。图中:F1为垂直且指向圆环内表面的分布力的合力,其分布集度设为q1(θ),分布范围为[-β1,β1];F2为垂直且指向圆环外表面的分布力的合力,其分布力集度为q2(θ),分布范围为[-β2,β2]。
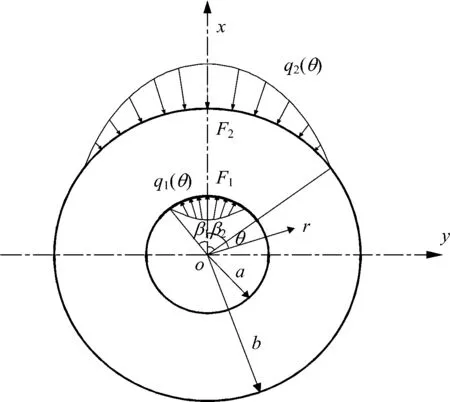
图4 混凝土圆环的受力状态简化模型
根据混凝土圆环受力平衡条件,有
F1=F2
(1)
其中,
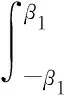

式中:t为钢板厚度。
借助于Airy应力函数Φ可以得到满足采用极坐标(r,θ)表示的相容方程为
(2)
应力边界条件为
(3)
式中:σr和τrθ分别为混凝土圆环沿径向和环向的应力。
q1(θ)和q2(θ)关于x轴对称分布,都是偶函数,可以展成傅里叶级数为
(4)
式中:A0,Ai,B0和Bi为待定系数,且有
(5)
假设q1(θ)和q2(θ)为按抛物线形式分布,则可以表示为
(6)
式中:q10和q20为分布载荷的极大值。
由式(6)和式(1),可以得到q10和q20之间的关系为
(7)
将式(6)代入式(5)中,即可得到傅里叶系数Ai和Bi。
2.2 应力解
在确定傅里叶系数Ai和Bi后,求解式(2),得到其通解为
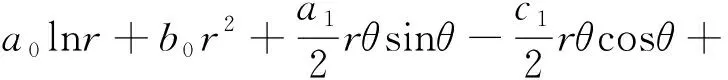
(8)

由于整环的位移是单值的,可得
(9)
式中:μ为泊松比。
根据余弦函数的对应系数相等条件以及位移单值条件式(9),并结合应力边界条件式(3)和傅里叶级数式(4)等条件,可以求得用傅里叶系数表示的待定系数,分别为
a1=A1a

c1=0,d1=0
an=-0.5a2b2(nBna2nb2+n+Ana3n+2-nAnanb2n+2+nAnan+2b2n-Anan+2b2n-nBna2n+2bn-Bna2nbn+2+Bnb3n+2)×[-n2a2nb2n(a2-b2)2+a2b2(a2n-b2n)2]-1(n-1)-1
bn=0.5(nBna2nbn+4+nAnan+4b2n-nBna2n+2bn+2-nAnan+2b2n+2-Anan+2b2n+2-Bna2n+2bn+2+Bna2b3n+2+Ana3n+2b2)[a2b2(a2n-b2n)2-n2a2nb2n(a2-b2)2]-1(n+1)-1
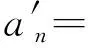
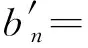

确定待定系数后,代入式(8)可得应力函数。
应力解根据参考文献[10],采用弹性力学极坐标中应力分量的经典表达式[10]为
(10)
式中:σθ为混凝土圆环的切向正应力;σz为垂直于混凝土圆环的法向应力。
将已确定待定系数的应力函数代入式(10)即可得到混凝土的应力分量。
2.3 位移解
各个位移和应变分量可以在应力分量确定后,根据弹性力学平面应变问题的物理方程和几何方程确定。
弹性体的位移可以分为变形位移和刚性位移2部分。所以有
(11)
式中:ur为径向总位移;uθ为切向总位移;ur1为变形径向位移;uθ1为变形的切向位移;ur2为刚性径向位移;uθ2为刚性切向位移。
ur1和uθ1通过积分得到,有
(12)
式中:εr和εθ分别为径向应变和切向应变。
极坐标下的表达式为
(13)
式中:kx和ky分别为直角坐标系中的平移量;k3为绕z轴的旋转量。
假设在内表面极坐标(a,π)位置只约束圆环的环向位移,而在(a,0)位置约束圆环的环向位移和径向位移,则位移边界条件为
(14)
考虑圆环位移边界条件、应力边界条件以及几何形状的对称性,可知uθ2为奇函数,ur2为偶函数,则有ky=0,k3=0。
对式(13)进一步简化为
(15)
位移最终表达式为
(16)
将式(16)代入式(14)求解出kx。
3 贯穿钢筋的力学分析
若梁上所受分布载荷集度为q(x),则由梁的挠曲轴近似微分方程为
(17)
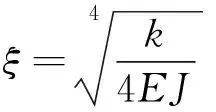
式中:ζ为梁和地基的弹性性质相关的综合参数;w为任意一点的挠度;EJ为抗弯刚度。
当q(x)不超过x的3次幂时,式(17)的通解为
w=-e-ξx[C1cos(ξx)+C2sin(ξx)]+
(18)
式中:k为基础弹性系数;C1,C2,C3和C4为待定系数。
以着力点为坐标原点,除原点附近的着力区域外,载荷集度q(x)=0。且由于结构的对称性,只选取着力点右边的半段分析。
梁的挠度及内力在离开着力点相当远处均应趋于0,即C3和C4为0。
着力点处挠曲轴的切线在对称基础反力和载荷作用下应为水平,即当x=0时,有

(C1-C2)cos(ξx)]=0
(19)
所以C1=C2。
由此,梁在任一截面x处的挠度ω、转角φ、弯矩M和剪力Q的计算式为
(20)
当x=0时,式(20)简化为
(21)
进而可以算出钢筋的最大弯曲应力σmax和最大剪切应力τmax分别为
(22)
4 算例分析
桥梁中钢混结合段中PBL剪力键的混凝土采用C50,泊松比μ=0.20,弹性模量为EC=34.5 GPa,钢板厚度为30 mm,开孔半径b=30 mm,PBL剪力键的钢筋半径为a=8 mm,弹性模量为Es=206 GPa。假设该PBL剪力键在弹性阶段的承载力为12.6 kN,混凝土榫与钢板和钢筋接触应力的接触范围均为[-π/2,π/2],亦即β1=β2=π/2,则根据式(1)、式(6)和式(7)计算出q10=32.40 N·mm-1,q20=8.64 N·mm-1。基础系数k=115 N·mm-3,ζ=0.029 mm-1。
为了验证本文钢混组合结构中PBL剪力键在工作状态下的弹性静力解析解的正确性,在用该文推导的解析解求解的同时采用ANSYS建立有限元模型进行对比分析。
采用ANSYS建立有限元模型时,混凝土圆环采用PLANE42单元,环向网格按每1.5°的角度进行划分,同一单元径向网格尺寸与环向网格尺寸近似相等。混凝土圆环的有限元模型如图5所示。

图5 混凝土圆环的有限元模型
图6给出了解析解和数值解得到的θ分别为0°,45°,90°,135°和180°时混凝土圆环的径向位移曲线,径向位移的方向以沿半径向外为正。由图6可以看出:随着离开圆心距离的增大,混凝土圆环在θ=0°方向上的径向位移快速增加;混凝土圆环径向位移在θ大于90°后基本不随离开圆心距离的变化而变化。各点径向位移的解析解与数值解吻合程度都较好,其中混凝土圆环在θ=0°,r=30 mm位置径向位移最大,相对误差为0.12%。

图6 圆环的径向位移
θ=0°和θ=180°时,由于结构的对称性,环向位移为零,混凝土圆环在θ为45°,90°,135°方向上(位移方向以顺时针为正)数值解和解析解得到的环向位移曲线如图7所示。由图7可以看出,随着离开圆心距离的逐渐增加,环向位移在θ=45°和θ=90°方向上的变化较在θ=135°方向上变化大。各点环向位移的吻合程度都比较好,其中在θ=90°,r=30 mm位置环向位移最大,相对误差为1.20%。
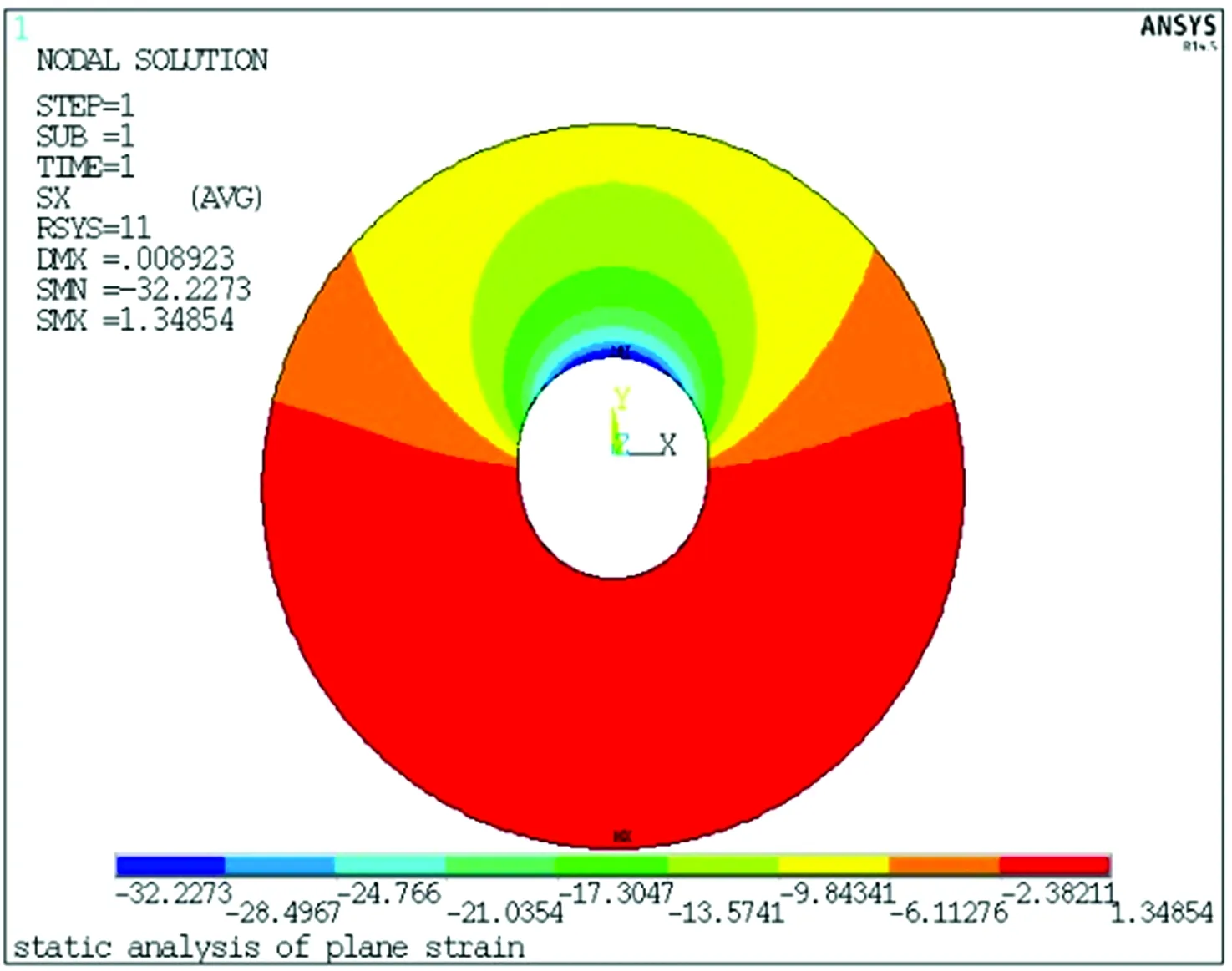
θ分别为90°,135°和180°时的径向应力较小,因此图8只画出了θ=0°和θ=45°时解析解和数值解得到的径向压应力曲线。由图8可以看出,随着离开圆心距离的增加,0°和45°方向上径向应力逐渐减小,减小速率逐渐减缓。各点径向应力的吻合程度都较好,其中在θ=0°,r=8 mm位置径向应力最大,相对误差为2.50%。

图7 圆环的环向位移

图8 径向应力
θ分别为0°,45°,90°,135°和180°时解析解和数值解得到的环向应力(以受拉为正)曲线如图9所示。由图9可以看出:0°,45°和90°方向上的环向应力相差较大,而135°和180°方向上的环向应力相差不多。各点环向应力的吻合程度都较好,其中在θ=90°,r=30 mm位置环向应力最大,相对误差为0.15%。

图9 环向应力
径向位移云图、环向位移云图、径向应力云图和环向应力云图如图10—图13所示,各物理量与图6—图9具有一致的分布规律。
C50混凝土抗压强度标准值fck=32.4 MPa,由图12得知混凝土圆环的最大应力为32.23 MPa,未超过fck,说明混凝土材料处于弹性范围之内。

图10 混凝土圆环径向位移云图(单位:mm)

图11 混凝土圆环环向位移云图(单位:mm)
对于贯穿钢筋,根据式(19)和式(20),可计算得出:w=-0.097 mm,φ=0,M=108.62 N·m,Q=-6.3 kN,σmax=270 MPa 贯穿钢筋强度满足要求。 根据现有钢混凝土组合结构的设计理念,在正常使用阶段,PBL剪力键大多工作在弹性阶段,非线性问题并不突出。因此,根据正常工作状态下的受力特性,钢混结合段中单个PBL剪力键的弹性受力,可以简化为贯穿钢筋的Winkler弹性地基梁和混凝土圆环的平面应变问题。建立简化力学模型,应用Airy应力函数,求解相应的解析解,通过与有限元分析结果的对比证明了其可靠性。 图12 混凝土圆环径向应力云图(单位:MPa) 图13 混凝土圆环环向应力云图(单位:MPa) 本文方法在PBL剪力键工作状态处于线弹性变形阶段时有很好的适用性。所得到的混凝土圆环和贯穿钢筋受力分析的解析解为PBL剪力键在工作状态下的传力机理的研究、结构优化设计、提高承载能力提供了理论依据和计算方法,同时为PBL剪力键在非线性工作状态下受力分析和求解解析解的研究打下了理论基础。5 结 语