基于带隙性能评价函数的特征频段隔振周期排桩选型

姜博龙，刘维宁，马 蒙，李明航

(北京交通大学 土木建筑工程学院，北京 100044)

随着轨道交通路网的加密，运行列车引起的环境振动问题也愈加凸显。它对沿途居民的日常生活、精密仪器的正常运转和文物古建的保护都造成了一定的影响。当轨道减振和敏感建筑被动隔振无法彻底解决振动问题时，作为综合减隔振措施中重要一环的传播路径隔振具有不可替代性。

排桩作为典型的非连续波屏障，应用在传播路径隔振中，凭借其造价低、耐久不易损坏、隔振效果好等优势，受到国内外学者广泛关注，并针对其展开了大量研究。现有的针对隔振排桩的研究集中在波场求解方法方面，通常采用二维简化模型对体波进行求解而采用三维数值模型对表面波进行求解[1-5]。这些研究考虑到的桩数目较少或仅仅是单排，且忽视了其周期性。直到石志飞等[6]充分考虑了群桩的周期性，将周期结构带隙理论引入到工程隔振领域，为解决环境振动问题提供了新的思路和依据。周期结构对通过它的振动波具有选择透过性，无法透过其传播的振动波所处的频带被称为禁带或带隙[7]。黄建坤[8-10]采用平面波展开法求解周期排桩带隙，以首阶完全禁带的起、止频率以及对应的带宽作为评价指标，对周期排桩首阶带隙分布影响因素进行了分析；刘心男[11]对比了二维和三维模型中周期排桩对带隙范围内振动的衰减结果，发现随着桩长的增加，三维数值结果逐步收敛于二维数值结果；蒲兴波[12]提出了一种新的表面波识别方法，用于获取二维土—周期排桩系统的面波带隙。

目前对于周期排桩的带隙描述、影响因素分析和作用效果评价主要是采用首阶禁带的起、止频率以及对应的带宽3个指标。周期排桩的隔振效果不仅与初始带隙相关，与各阶带隙的分布也有关系。另外，目前周期排桩带隙影响因素分析和结构优化选型都没有充分考虑被阻隔对象特征，造成了结构优化选型针对性不强。因此，针对轨道交通环境传播路径隔振，本文提出以周期排桩带隙性能评价函数Φ为单一指标、并考虑带隙分布的选型方法。

1 隔振周期排桩带隙计算

对周期排桩带隙的求解可根据固体物理晶格理论[13]进行简化：周期排桩可由某一根单桩通过周期性和对称性的拓扑变换获得，因此，计算时仅需以某一单桩作为基本单元，并对其施加周期边界进行研究。根据周期结构带隙产生机理的不同，隔振周期排桩可分为散射型排桩和局域共振型排桩，二者对应的基本单元如图1所示，图中：A，B，C分别代表土体、桩和填充体；R为桩半径；r为填充体半径；a为周期常数。

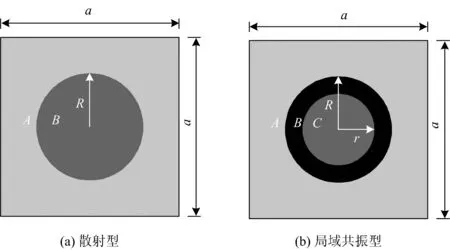
图1 排桩基本单元平面示意图

下面利用平面波展开法[7]进行周期排桩带隙计算。土—周期排桩体系弹性动力学基本(维纳)方程为

(1)

其中，

u(d,t)=(uxuyuz)

式中：t为时间；d为位置矢量；u(d,t)为位移矢量；ux,uy,uz为沿x,y,z方向的位移分量；ρ(d)为密度函数；λ(d)和μ(d)为与位置矢量d相关的Lamé常数。

由于密度函数ρ(d)，与位置矢量d相关的Lamé常数λ(d)和μ(d)在空间分布呈现周期性，故其可在倒格矢空间按傅里叶级数展开，为叙述方便，统一采用f来表示这3个材料参量，有

(2)

其中，

式中：i为虚数单位；G1为对应各组元材料参数分布场内的倒格矢；f(G1)为傅里叶系数；S为基本单元面积。

对于散射型周期排桩，有

(3)

其中，

式中：η为桩占整个基本单元的填充比；P(G)为结构函数； J1为第一类第1阶的贝塞尔函数。

对于局域共振型周期排桩，有

(4)

其中，

式中：ηB，ηC，ηf分别表示桩、填充体以及散射体(填充体+桩)占整个基本单元的填充比；P(G1)，Ph(G1)为结构函数。

式(1)的解为

(5)

式中：ω为角频率；G2为位移场中的倒格矢；K为限制在第一Brillouin区内的Bloch波矢；uK(G2)为与各材料参数具有相同周期的Bloch调幅函数。

将式(2)和式(5)代入式(1)，可得本征方程为

(6)

G2)(K+G2)(K+G3)uz(K+G2)

(7)

其中，

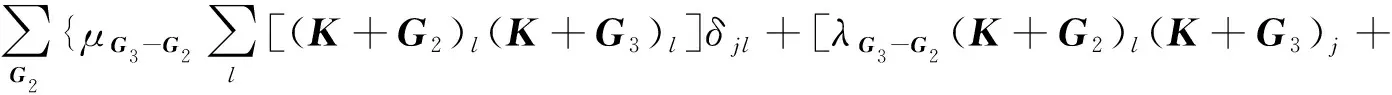
μG3-G2[(K+G2)j(K+G3)l]}

j=x,y；l=x,y

G3=G1+G2

式中：ux(K+G2)，uy(K+G2)和uz(K+G2)为沿x，y和z方向的位移分量；δjl为克罗内克函数。

令波矢K扫略第一不可约布里渊区便可得到整个结构的频散曲线和带隙特性[7]。

下面用1个具体算例验证该计算方法，选取文献[14]中的周期排桩。该排桩为圆截面实心桩结构，拓扑形式为正方晶格，排桩类型为散射型，周期常数a=2 m，桩的半径R=0.65 m，具体材料参数参见表1。

表1 土—桩系统的材料组成及物理力学参数

图2给出了本文和文献[14]计算带隙的结果。二者均在33.3～37.3 Hz存在1个完全带隙。二者计算结果的吻合证明了本文方法的正确性。

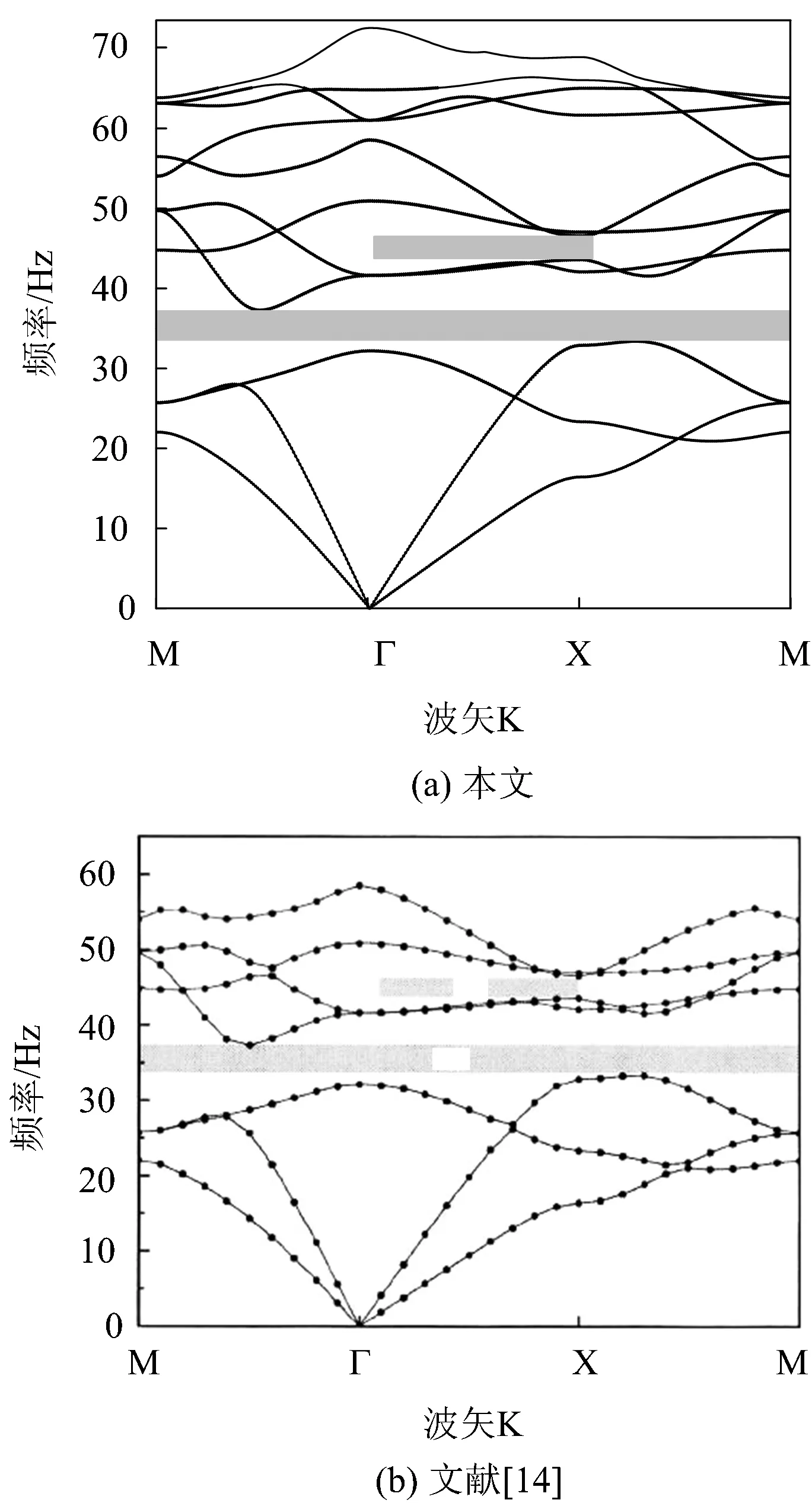
图2 本文和文献[14]计算的带隙结果

2 能带结构带隙性能评价函数

图3给出了2种典型周期排桩的带隙计算结果，图3(a)为按照六角晶格布置的散射型排桩，周期常数为4 m，混凝土桩半径为1.2 m；图3(b)为按照六角晶格布置的局域共振型排桩，周期常数为3 m，混凝土桩半径为1 m，橡胶填充体半径为0.4 m。

目前对于周期排桩的带隙描述、影响因素分析和作用效果评价主要是采用首阶禁带的起、止频率以及对应的带宽3个指标。由图3可见，散射型排桩的首阶带隙起始频率低于局域共振型排桩，且首阶完全带隙的带宽要宽于局域共振型排桩；但局域共振型排桩80 Hz以下带宽总和却大于散射型排桩。因此，对于周期排桩的带隙描述、影响因素分析和作用效果评价不能只关注于首阶完全带隙，也要综合考虑关心频段内各阶带隙的分布情况。

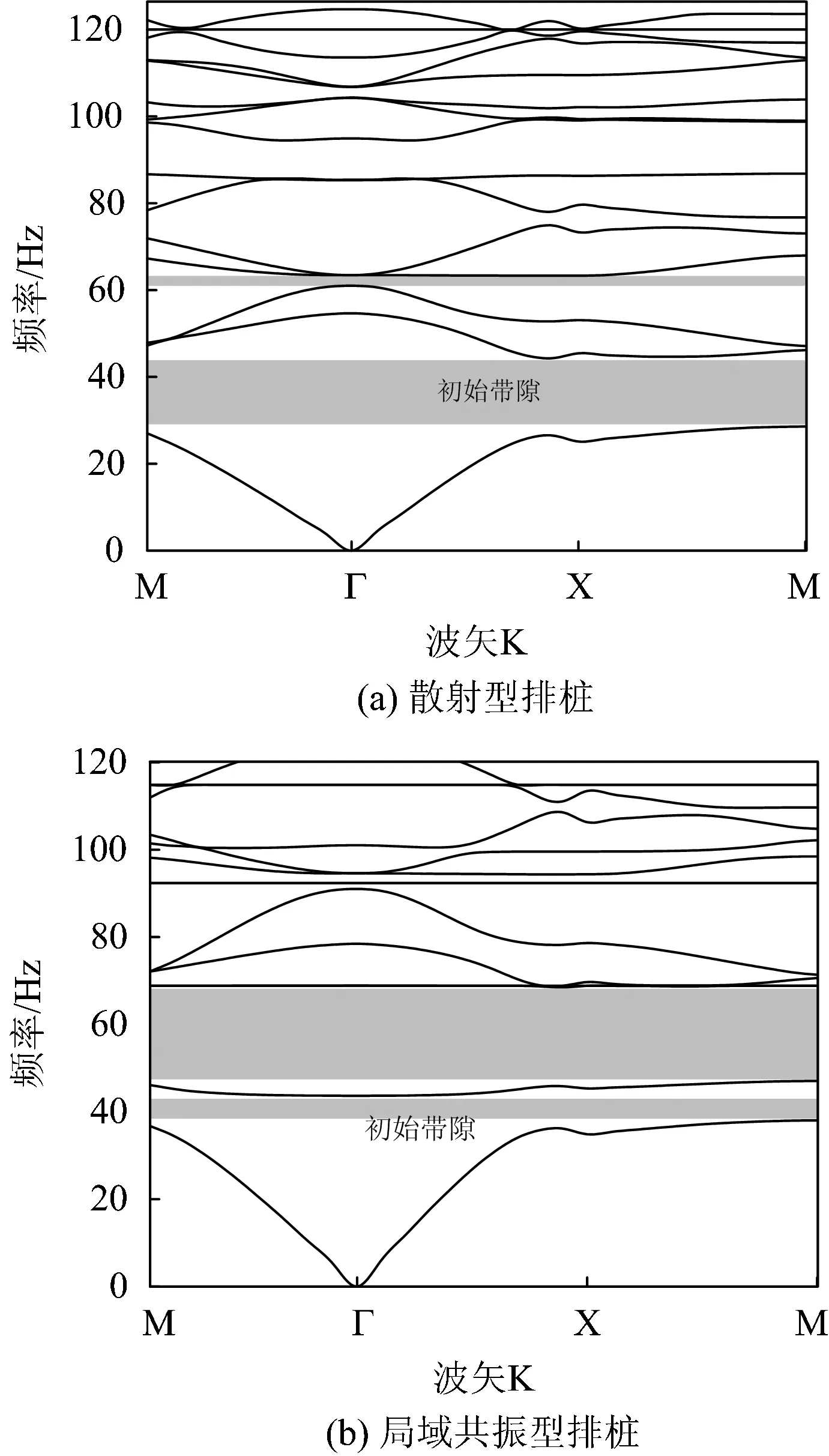
图3 典型六角晶格布置排桩的带隙分布对比

带隙具备2个典型特征，一个是中心频率，另一个是带宽。图4为被阻隔对象显著频率与周期隔振结构带隙分布关系示意图。被阻隔对象的显著频率为63 Hz，图中带隙1和带隙2分别为2种周期隔振结构的带隙分布。从图4可以看出，与带隙2相比，具有带隙1的周期隔振结构的带隙中心频率更加接近被阻隔对象振动的显著频率，但是带宽却较窄。因此若想取得良好的隔振效果，需要使周期隔振结构的带隙中心频率贴近被阻隔对象的显著频率，且带宽较宽。

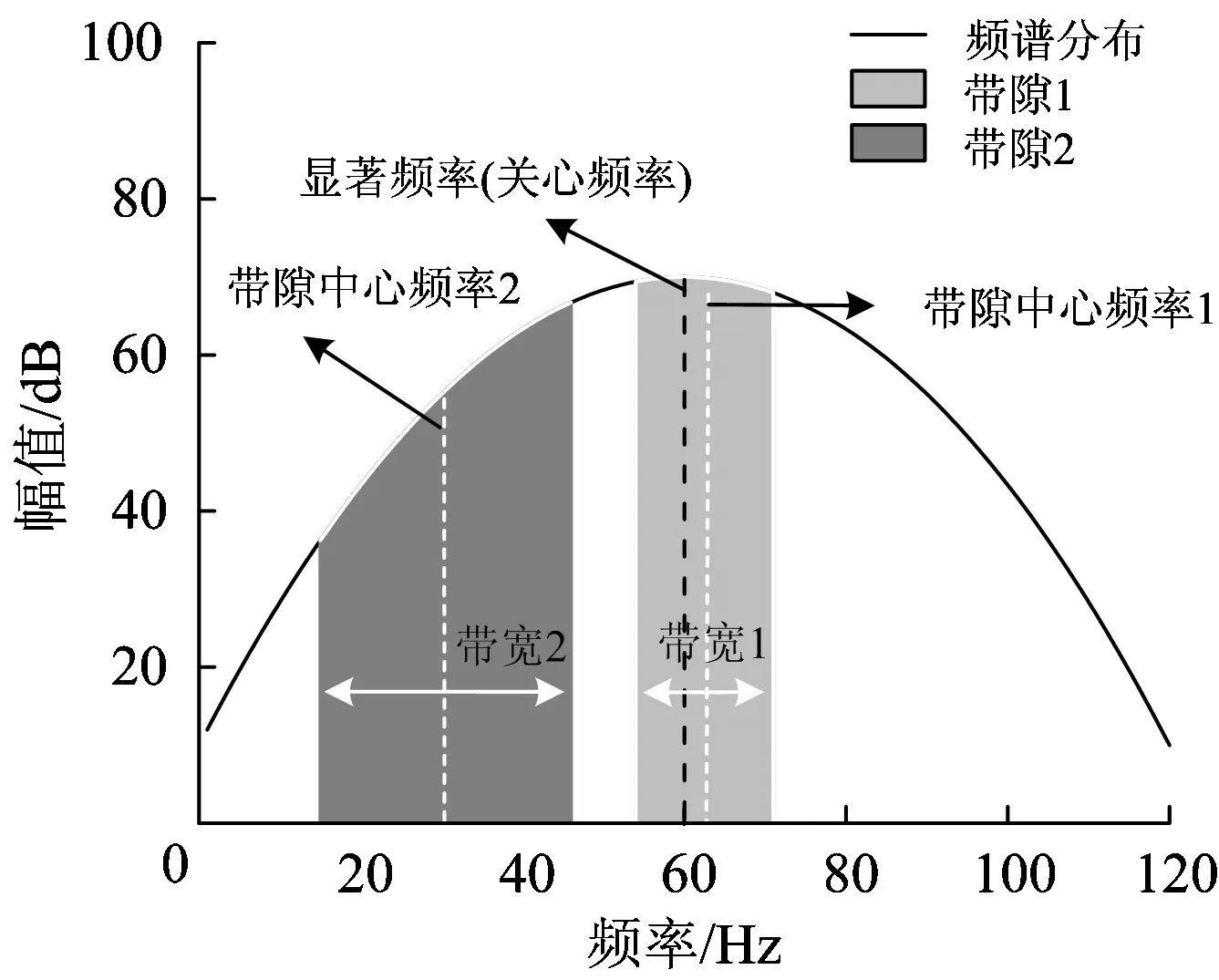
图4 被阻隔对象显著频率与周期隔振结构带隙分布关系示意图

基于上述分析，提出一种综合考虑被阻隔对象振动特征、隔振排桩各阶带隙分布的周期排桩带隙性能评价函数Φ为

(8)

式中：n为带隙数目；ωj为出现带隙的下限频率；ωj+1为同一带隙的上限频率；(minωj+1-maxωj)为该带隙的带宽；(minωj+1+maxωj)/2为该带隙的中心频率；ωD为需要阻隔的关心频率。

随着带隙中心频率逐步逼近需要阻隔的关心频率ωD，|ωD-(minωj+1+maxωj)/2|将取得极小值，同时随着带隙(minωj+1-maxωj)的增大，周期排桩带隙性能评价函数Φ将取得极大值，Φ值越大表征该结构形式越适用于被阻隔对象的显著频率的振动阻隔。

3 轨道交通特征频率隔振周期排桩选型

本文以东单地铁站到建国门地铁站区间隧道列车运行引起环境振动为研究背景[16]进行传播路径隔振周期排桩选型。

该段地铁隧道初衬厚度为0.25 m，所采用的混凝土的弹性模量为28.5 GPa，泊松比为0.2，密度为2 450 kg·m-3，材料阻尼比为0.02。二衬厚度为0.3 m，二衬混凝土的弹性模量为30 GPa，泊松比为0.2，密度为2 500 kg·m-3，材料阻尼比为0.02。隧道基底混凝土参数与二衬一致，列车采用常见的6节编组，经过测试断面的速度为60 km·h-1，扣件为普通DTⅥ2扣件。隧道埋深与地层相对位置关系如图5所示，地层信息参考表2。

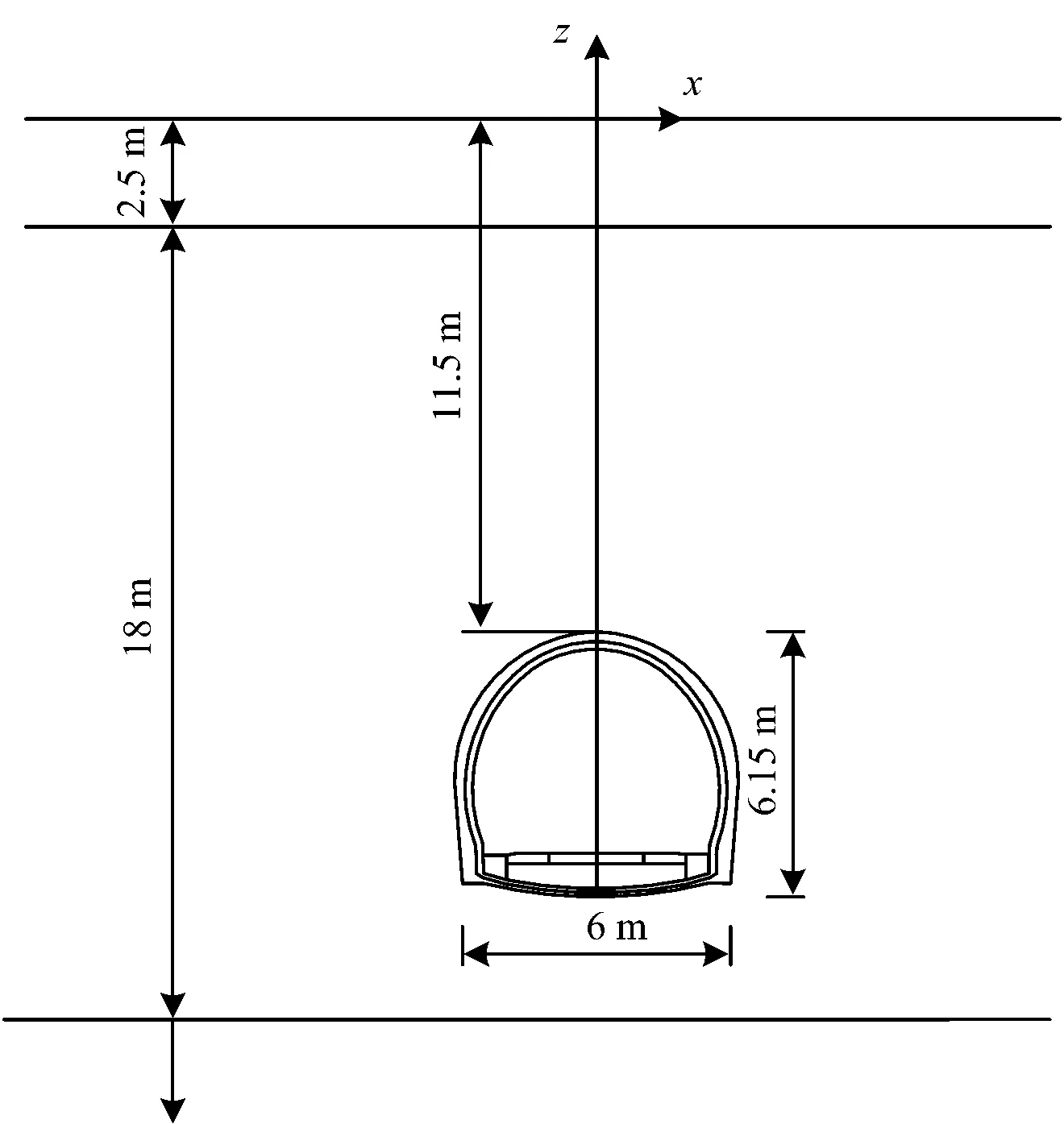
图5 隧道与地层相对位置[16]

土体类型厚度/m剪切波速/(m·s-1)压缩波速/(m·s-1)动弹性模量/(MN·m-2)动泊松比密度/(kg·m-3)阻尼比杂填土 2.5173.3356.5138.80.3501 6500.05粉质黏土 18.0235.0472.6308.00.3272 0100.04卵石和圆砾332.0620.0670.00.2862 0500.03

对该断面进行地表环境振动监测时测得的距离隧道中心线40 m位置处的地表竖向振动响应如图6所示。由图6可以看出，DTVI2扣件轨道型式下地铁列车以60 km·h-1速度运行引起的地表竖直方向振动峰值出现在63 Hz，此频率为轨道和扣件系统的自振频率。因此以该竖直方向振动的峰值频率63 Hz作为关心频率，即ωD=63 Hz。

隔振周期排桩选取按照正方晶格和六角晶格2种典型晶格类型布置的散射型排桩和局域共振型排桩，其布置如图7所示。

根据文献[15]可知，排桩埋深一般到粉质黏土层底部可取得较好效果，鉴于隧道也埋置于粉质黏土层，且排桩所在地层中粉质黏土的含量占比为主(约90%)，本文计算以粉质黏土—周期排桩的带隙性能评价函数Φ作为选型依据。相应材料参数见表3。

图6 距离隧道中线40 m处地表振动加速度响应测试值

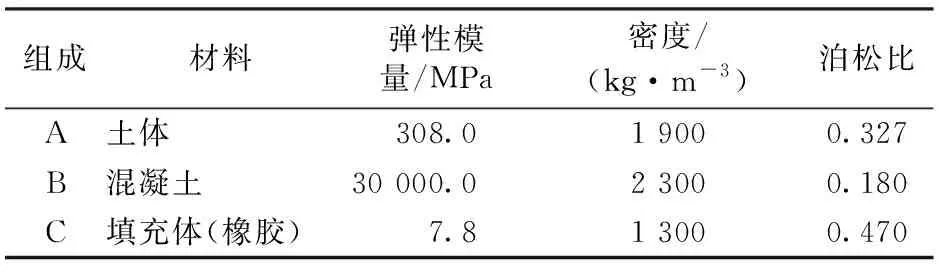
组成材料弹性模量/MPa密度/(kg·m-3)泊松比A土体308.01 9000.327B混凝土30 000.02 3000.180C填充体(橡胶)7.81 3000.470

选取14种周期排桩进行优化选型，14种周期排桩的具体情况及对应的带隙性能评价函数Φ值见表4。由表4可见， 5号周期排桩的Φ值最大，说明5号周期排桩最适宜用于隔离以竖直方向63 Hz为关心频率的环境振动。

图7 不同晶格类型布置的排桩

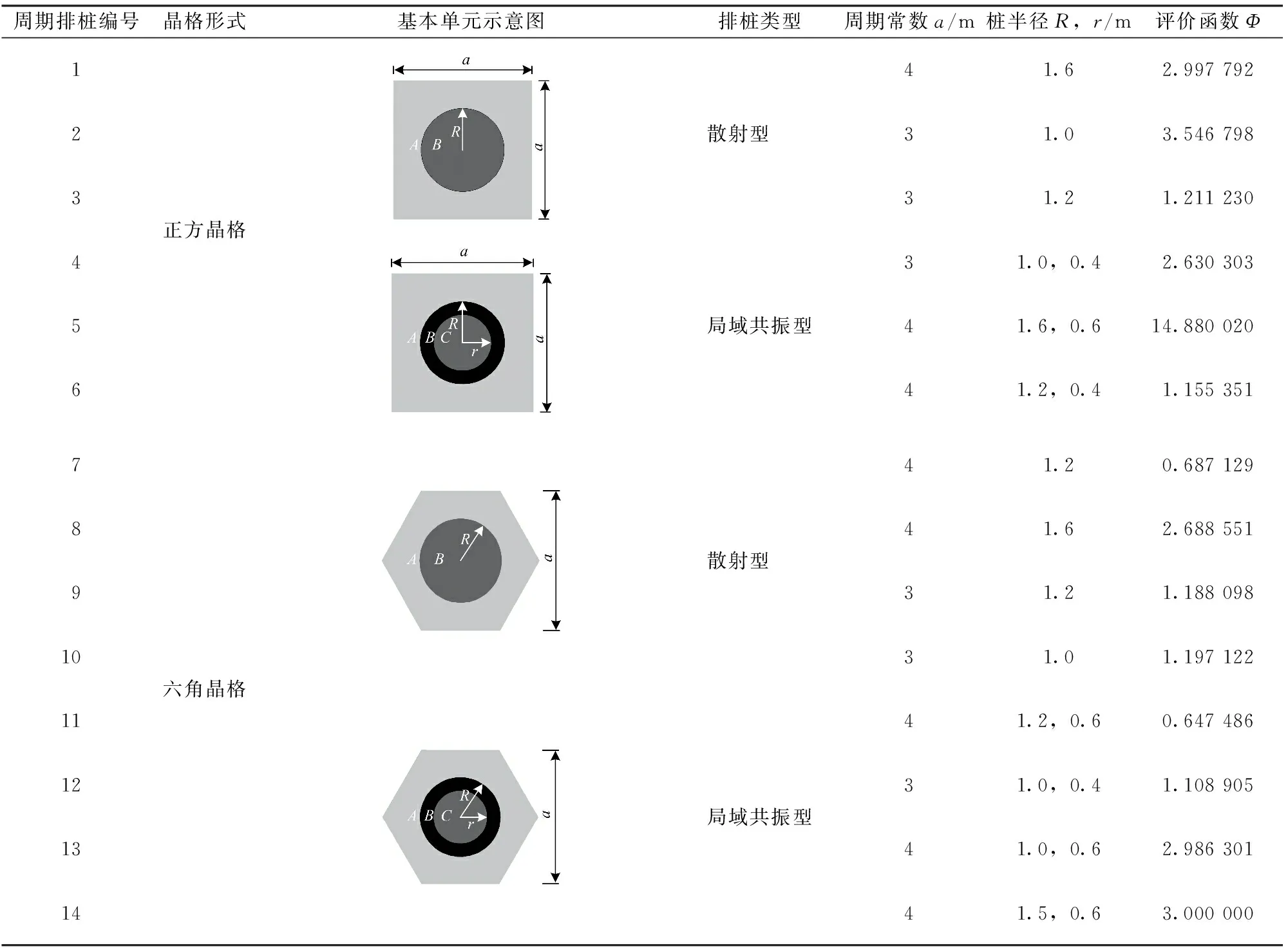
表4 各周期排桩的具体情况及对应的带隙性能评价函数Φ值

图8给出了5号周期排桩分别在杂填土和粉质黏土中的带隙分布图。从图8可以看出，5号周期排桩在其穿过的2层土体中都有带隙覆盖63 Hz的关心频率，且在80 Hz以下带宽分布范围较大。

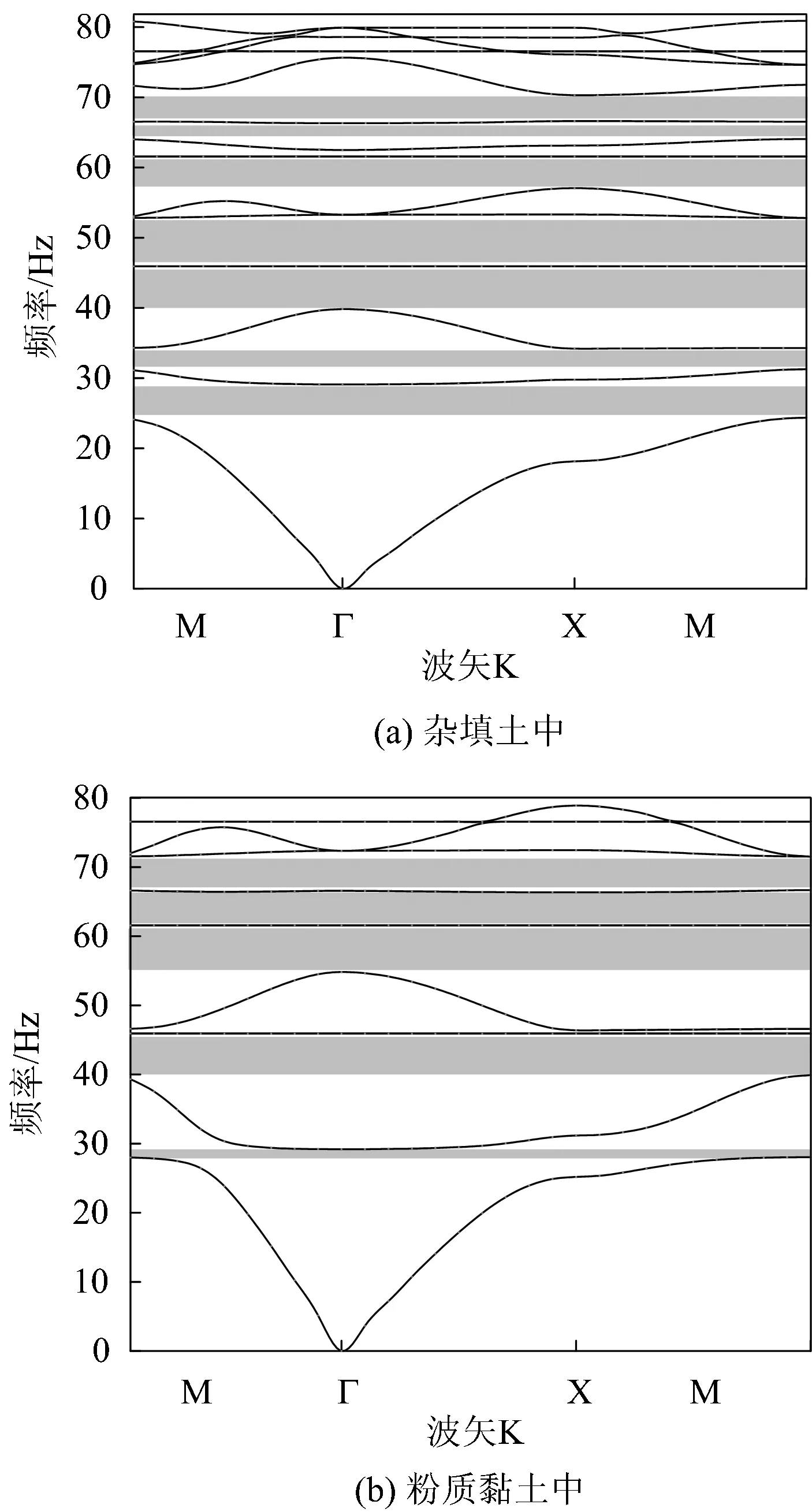
图8 5号周期排桩竖直方向带隙分布

4 结果验证

运用ABAQUS软件，以前文提到的工程资料建立隧道—地层—周期排桩耦合的三维动力有限元分析模型(图9)进行轨道交通环境振动传播路径隔振周期排桩的隔振效果分析，验证第3节中选型结果的有效性。地层参数见表2，模型尺寸为100m×60 m×24 m，土体、隧道及排桩均采用实体单元模拟，在隧道基底上输入的激励为采用周期性车辆—轨道耦合解析模型[16]计算得到的扣件反力时程，边界设置为弹簧阻尼吸收边界。

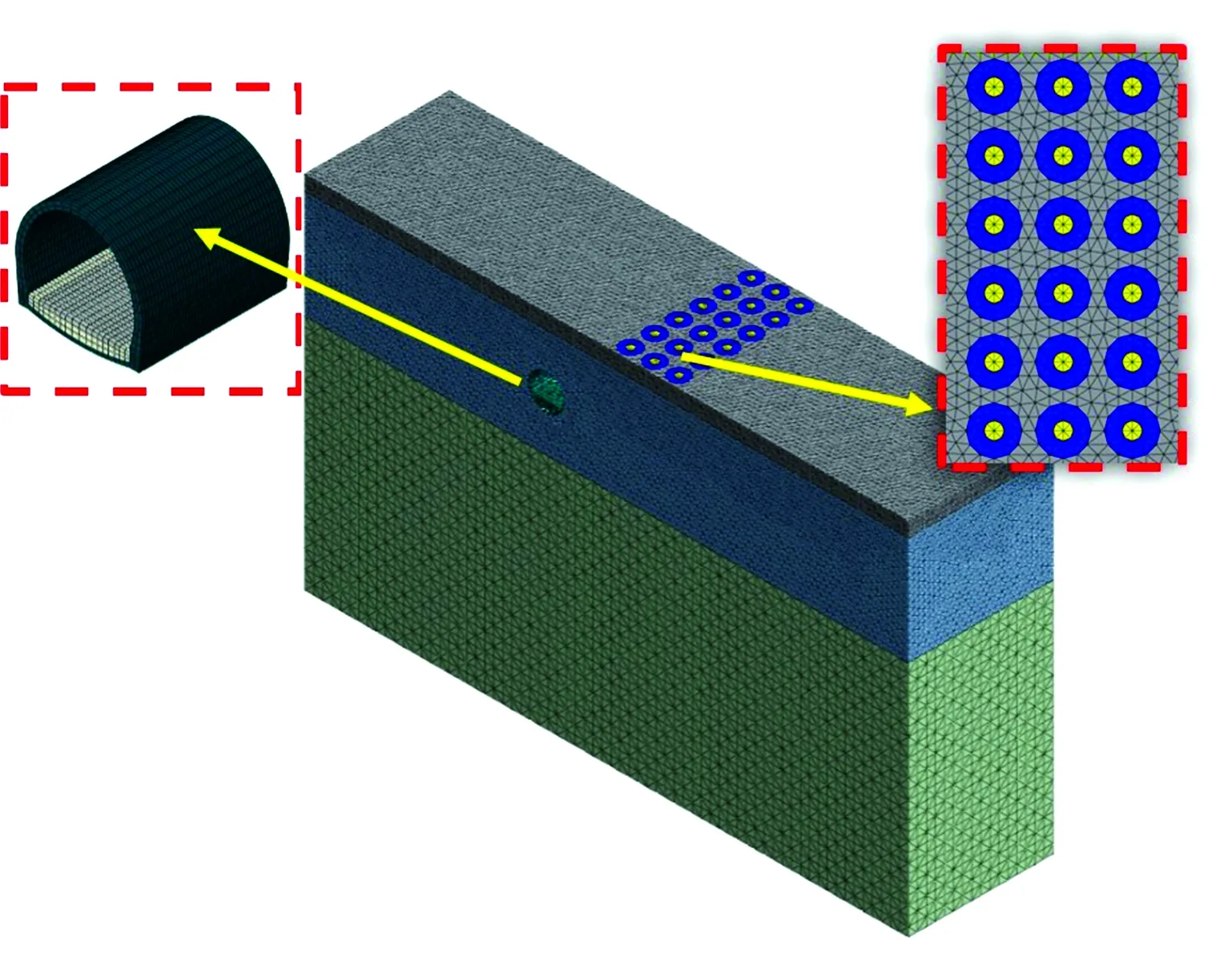
图9 三维动力有限元模型

采用加速度振幅衰减系数Ar[17]评价排桩隔振性能为

(9)

式中：a1和a2分别为隔振排桩后某点的加速度幅值与同一位置处无隔振排桩的加速度幅值。

Ar→0表明结构具有良好的隔振性能。

图10为5号周期排桩后距离隧道中心线40 m位置(与实测点对应)处的振幅衰减系数及其带隙分布。

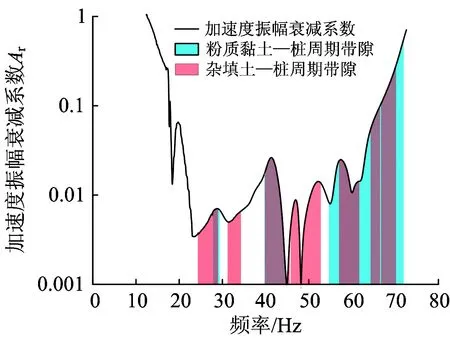
图10 距离隧道中心线40 m处振动加速度振幅衰减系数及其带隙分布

由图10可以看出，带隙范围内2层土体的振动都有较好的衰减，说明5号排桩隔振效果明显，也间接证明了带隙计算结果的正确性与选型方法的有效性。

5 结 语

本文提出了基于带隙性能评价函数的轨道交通特征频段隔振周期排桩的选型方法，性能评价函数作为单一评价指标综合考虑了带隙带宽、中心频率2个因素，规避了多指标分析的不确定性；其次，将轨道交通环境振动的显著频率作为关心频率引入该函数，充分考虑了被阻隔对象的振动特征。该方法不再单独以首阶带隙为选型依据，综合考虑了各阶带隙的分布情况。本文通过建立三维动力有限元模型对选型结果进行了验证，选出的隔振周期排桩在带隙分布范围内有较好的隔振效果。