由超辐射引起的迁移率边和重返局域化*

吴瑾 陆展鹏 徐志浩 郭利平

(山西大学理论物理研究所,量子光学与光量子器件国家重点实验室,太原 030006)

1 引言

超冷原子气与腔量子电动力学分别是凝聚态物理与量子光学中最重要的研究领域之一,它们有着各自的发展历史与丰富成果[1,2].冷原子气体与光腔的耦合系统进一步结合了这两大领域,为模拟和研究各种新奇量子物态提供了一个重要平台[3,4],引起了人们的广泛关注.在单模腔中的玻色爱因斯坦凝聚体加入横向泵浦会导致体系从正常相转变为超辐射相[5].而在超辐射相区内,腔内原子将受到一个腔诱导的超晶格势作用[6].实验上已经观测到在腔诱导的公度超晶格中存在超固体相[7,8].当腔诱导的晶格势与静态光晶格势是非公度的,在平均场近似下系统形成一个有效的准周期调制,导致金属-绝缘的转变[9-11].

另一方面,在这种既不是周期的,又不是完全无序的准周期系统中,最典型的模型就是具有准周期调制的一维Aubry-André (AA)模型,它展现了独特的局域化性质[12,13].由于AA 模型的自对偶特征,具有与能量无关的局域化转变,即在某一准周期调制强度下,所有的单粒子态要么都是局域的,要么都是扩展的.2008 年,Roati 等[14]在冷原子体系中利用双色光晶格的方案已经实现了准周期调制的AA 模型,并且观测了其局域化转变.但值得注意的是,通过破坏自对偶特性,一维准周期调制系统中可以出现迁移率边[15-19],即扩展态与局域态之间的能量边界.最近,理论上预测了长程跃迁的准周期调制系统[20]、具有特殊形式准周期调制的系统[21]、准周期调制的玻色子对系统[22]以及二维非厄米准晶[23]等具有简洁解析形式的迁移率边.通常来说,无序系统经过局域相变后,随着无序强度的进一步增强,所有的态始终处于局域态.然而,最近Roy 等[24]研究了一维交叉调制的二聚体准晶系统,发现由于二聚体和准周期调制的竞争,导致重返局域化现象的产生,即部分态在特殊的无序强度范围内从局域态重新变成扩展态,随着无序强度进一步增强,所有态又重新回到局域态的现象.这一现象在非厄米准周期系统也被发现[25].重返局域化现象可以利用激发动力学手段探测[26].通常的冷原子实验中,实现具有重返局域化现象的无序模型存在一定的困难.

基于以上的研究和存在的难题,本文讨论了在原子-光腔耦合系统中由超辐射引起的迁移率边和重返局域化,以及实验的实现方案.

2 理论模型

如图1 所示,考虑一团含有Nb个原子的玻色爱因斯坦凝聚体被捕陷在一个梯子形的光晶格中,并且此梯形光晶格处于x-y平面被装载进一个高精度腔中.每条梯子腿上的原子受到x方向上的周期势Vstatic=V1cos2(kx) 限制,其中V1正比于光格子强度和晶格波矢k.沿着z方向梯子腿加载波矢为kp、频率为ωp的泵浦光.在紧束缚近似下,系统的哈密顿量可以写为:

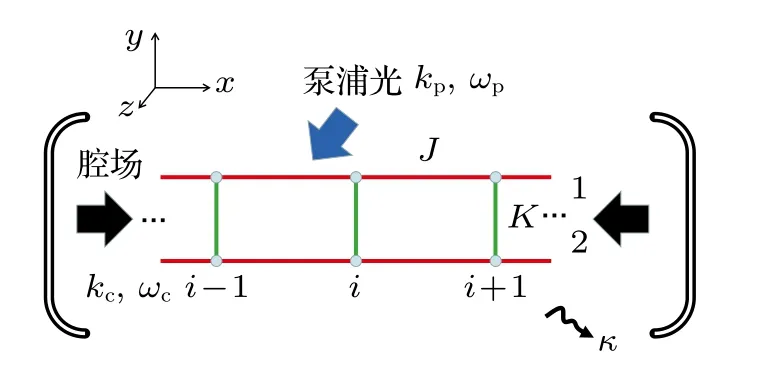
图1 实验装置示意图.在高精度腔中,中性原子被x-y 平面的梯子形光晶格俘获,并沿着z 方向加入驱动泵浦场.泵浦场的频率为 ωp 远失谐于原子能级跃迁频率 ωa,但接近于腔场频率ωcFig.1.A schematic diagram of experimental setup.In a high-finesses optical cavity,spinless atoms are trapped by a ladder lattice in x-y plane.The atoms are driven by a pump laser beam along z direction.The frequency ωp of the pump laser is far detuned from the atomic transition line ωabut close to the cavity-mode frequency ωc .

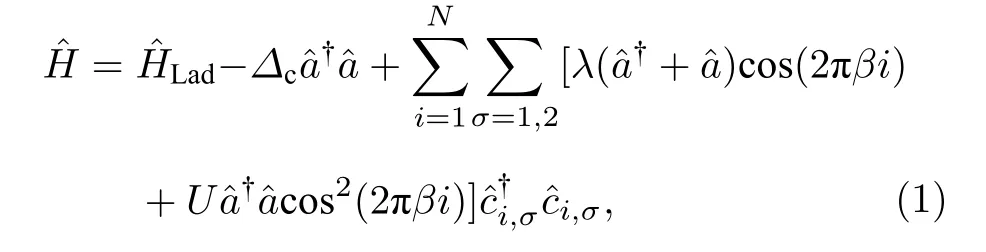
其中

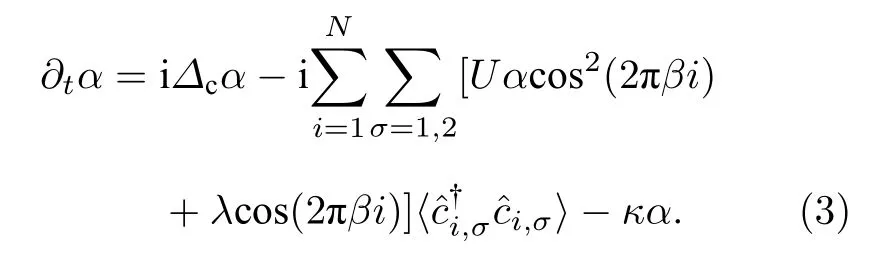
当κ ＞J时,腔场存在稳态解.腔场的稳态解(∂tα=0)可以写为:

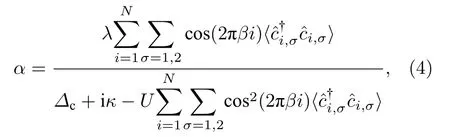
依赖于光场序参量α.当处于正常相(α=0)时,系统可以由一个标准的梯子模型所描述,而当系统进入超辐射相区(α0),一个由超辐射引起的调制势被引入到梯子模型.图2(a)给出了在L=1974,K=0.8,Δc=-2 和κ=1.2 时,对于不同U,光场序参量|α|随有效耦合强度λ的变化.对于不同的U,在小λ情况下,|α|=0,而随着λ的增加到超过某个临界有效耦合强度λc后,光场序参量|α|跳变为一个有限值,表明此时系统进入到超辐射相区.由图2(a)可以看出,随着U的增加,临界耦合强度λc的值逐渐增加.图2(b)给出了λc随着U值的变化情况,其中黑色实线为数值拟合结果,即λc=-0.1149U2+0.4251U+1.9875 .由此可见,通过调节腔场强度可以有效地控制超辐射转变点,从而实现对模型中调制强度λD和UD调节的控制.

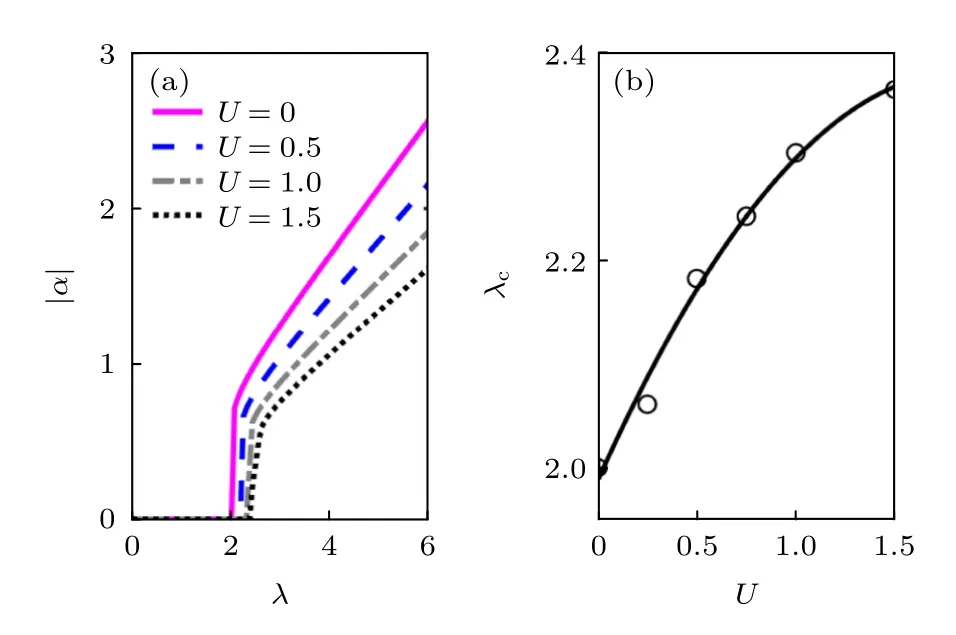
图2 (a) 腔场耦合强度U 取不同的值时,光场 |α| 随着耦合强度λ 变化的图像;(b) 临界耦合强度 λc 随着U 的变化情况.这里,L=1974,K=0.8,β=610/987,Δc=-2和κ=1.2Fig.2.(a) The cavity field |α| as a function of the pumping strength λ for different U;(b) the critical pumping strength λc as a function of U.Here L=1974,K=0.8,β=610/987 ,Δc=-2 and κ=1.2 .

3 结果与讨论

本节首先选取参数UD=1,2 作为具体的例子,通过改变不同的调制强度λD,分别讨论存在两种不同的局域化现象,即存在迁移率边和重返局域化.最后给出系统在λD-UD参数平面的局域化相图.

3.1 迁移率边

图3(a)给出了UD=1 和L=3194 时,〈IPR〉和〈NPR〉随着准周期调制强度λD的变化情况.对比AA 模型,此时系统的〈IPR〉和〈NPR〉并不是在同一点发生转变,而是存在了一段〈IPR〉和〈NPR〉同时具有有限值的临界相区,即图3(a)中灰色标记的区域.这一现象表明在的区间,体系能谱中应该同时存在扩展和局域态.这里,而当所有本征态随着λD的增加都变成局域态.图3(b)—图3(d)给出了在UD=1,对应于不同λD时,〈NPR〉随着尺寸L的标度分析.当λD=0.5 时,如图3(b)所示,在L →∞的极限下,〈NPR〉随着尺寸L的增大趋近于一个有限值,约为 0.445,表明系统中所有本征态都是扩展态.当λD=5 时,如图3(d)所示,,表明此时系统中所有的本征态都为局域态.当调制强度λD落在中间临界相区时,以λD=2为例,如图3(c)所示,〈NPR〉在L →∞时,随着L呈衰减趋势,并趋近于一个有限值,约为0.14,它远小于扩展相区的情况,表明此时系统中既存在扩展态又存在局域态,即存在迁移率边.

图3 (a) 当 UD=1,K=0.8,L=3194 时,〈IPR〉 (黑色实线) 和 〈NPR〉 (红色虚线) 随 λD 变化的曲线,灰色区域代表着具有迁移率边的临界区域;(b) λD=0.5,(c) λD=2,(d) λD=5 时,〈NPR〉 随着 L-1的变化,其余参数的取值是UD=1,K=0.8Fig.3.(a) 〈IPR〉 (the black solid line) and 〈NPR〉 (the red dashed line) as the functions of λD forUD=1,K=0.8,L=3194.The grey region denotes the critical region with mobility edges;〈NPR〉 as a function of L-1 withUD=1 and K=0.8 for (b) λD=0.5,(c) λD=2,and (d) λD=5 .

图4 (a1) λD=0.5,(b1) λD=2 和(c1) λD=5时第300 个激发态的密度分布;(a2) λD=0.5,(b2) λD=2 和(c2) λD=5 时第 1100 个激发态的密度分布.这里,K=0.8,UD=1和L=1220Fig.4.Density distributions of the 300th excited eigenstates for (a1) λD=0.5,(b1) λD=2,and (c1) λD=5 ;density distributions of the 1100th excited eigenstates for(a2) λD=0.5,(b2) λD=2,and (c2) λD=5 .Here,K=0.8 ,UD=1,and L=1220 .

图5 在 UD=1,K=0.8 和 L=3194 时,分形维度γ 随着调制强度 λD 和能量本征值 En 的变化.其中,黑色实线和黑色虚线分别对应了两个局域化转变点 和.图中颜色代表着γ 的大小Fig.5.γ of the eigenstates as a function of the energy spectrum and λD for UD=1,K=0.8,and L=3194 .Here the black solid line and black dashed line denote two transport points, and .The color code represents the values of γ.

3.2 重返局域化

通常来说,进一步增加调制强度λD,系统将一直处于局域区,如UD=1 时的情况.然而通过计算发现,在λD∈区 间,〈IPR〉和〈NPR〉又重新恢复到都保持有限值的情况,表明此时系统又重新进入到具有迁移率边的相区.这里,≈2.85 和而当λD＞系统又进入完全局域相.这是典型的重返局域化的特性.

重返局域化的特征可以由每个能量对应的本征态的分形维度γ随着λD的变化来精确地反映,如图6(b)所示.其中,4 条灰色实线从左到右分别对应于局域化转变点重返局域化现象指的是系统经过第一次局域转变,已经处于完全局域相后,随着调制强度的进一步增大,部分态再次回到扩展态;最终在更大的无序强度下,系统重新返回到完全局域相.从图6(b)可以直观地看出,时,所有态的γ值都趋于 1,系统处于完全扩展相.时,部分态的γ值趋于 0,部分态的γ值趋于 1,系统处于两种态并存的临界相区.在的区间内,所有态的γ都趋于 0,系统经历局域转变,已经处于完全局域相.而在区间内,部分本征态对应的γ的值趋于 1,代表着这些态重新回到扩展态,最终在后,所有态对应的γ都趋近于 0,系统又一次返回到完全局域相,该过程更加清晰地描述了重返局域化现象.

图6 当 UD=2,K=0.8,L=3194 时 (a) 〈IPR〉(黑色实线)和〈NPR〉 (红色虚线)随着 λD 变化的曲线,灰色区域表示具有迁移率边的临界相区;(b)分形维度γ 随着能量本征值 En 和调制强度 λD 的变化.图中颜色代表γ 的大小Fig.6.(a) 〈IPR〉 (the black solid line) and 〈NPR〉 (the red dashed line) as the functions of λD forUD=2,K=0.8,L=3194.The grey regions denote the intermediate regimes with mobility edges;(b) fractal dimension γ of all the eigenstates as a function of energies and λD forUD=2,K=0.8,and L=3194 .Here the color code represents the values of γ.

为了进一步验证重返局域化现象是否存在,在临界相区和局域相区,分别研究了〈NPR〉的标度变化.在图7(a)中,展示了λD=1,4 时,〈NPR〉随尺寸L变化的情况,可以看出当L →∞时,〈NPR〉均趋近于有限值,表明此时系统处于扩展和局域混合的临界相区.并且在热力学极限情况下,λD=1 时的〈NPR〉要比λD=4 时大很多,这表明系统处于λD=1时的扩展态所占比例要远大于λD=4 时的比例.而图7(b)展示了λD=2.5,5.5 时〈NPR〉随尺寸L的变化情况.可以看出,当L →∞时,〈NPR〉均趋于零,展示了完全局域的特性.由此可见,在UD=2时,随着调制强度λD的增加,系统出现了重返局域化现象.

图7 当 UD=2,K=0.8时平均参与率〈NPR〉 随 1/L 变化的曲线 (a) 临界相区;(b) 局域相区Fig.7.〈NPR〉 as a function of 1/L for UD=2,K=0.8 :(a) critical phase region;(b) localized phase region.

3.3 局域化相图

利 用〈IPR〉和〈NPR〉定义η=ln[〈IPR〉〈NPR〉],可以把临界相从完全的扩展和局域相中清晰地区分出来.这是因为在临界相时η的值大于-lnL,而处于完全扩展和局域的相时,η的值小于-lnL.图8(a)给出了λD-UD的平面内,以η的大小为填充颜色的相图.其中,白色区域代表了完全局域相或完全扩展相,红色区域代表了具有迁移率边的临界相,黑色实线对应于临界值≈1.97 .在本文所研究的调制强度UD的取值范围内,可以看到当UD＜时,系统随着λD的增大,从完全扩展相经历一个扩展态和局域态共存的临界相,最终转变到完全局域相.而当UD＞时,随着λD的增大,系统经历第一次局域转变到达完全局域相后,又重新回到临界相区,最终经历第二次局域转变到达完全局域相.因此,当UD＞时,体系中存在重返局域化现象.

图8 (a) λD-UD 参数平面内,以序参量η 的大小为填充颜色的相图,其中白色区域表示完全扩展或局域相,红色区域表示具有迁移率边的临界相.其中,绿色方块对应λ=3.183,Δc=-0.2 ,|α|=0.604 ,λD ≈2.86 ;黑色圆圈对应的是 λ=4.113 ,Δc=-0.6,|α|=0.607,λD ≈4.86 ;蓝色叉号对应于 λ=5.069 ,Δc=-2 ,|α|=0.608,λD ≈6.08.这里,κ=1.2,U=6,UD ≈2.21 .相图中的(b)绿色方块,(c) 黑色圆圈和(d) 蓝色叉号对应的参数取值下,所有态的逆参与率随本征能变化的情况.这里,K=0.8和L=1974Fig.8.(a) Phase diagram in the λD-UD plane.The color code represents the values of η,where the white regions denote the full extended or localized phase and the red region represents the critical phase.Here,the green square corresponds to λ=3.183 ,Δc=-0.2 ,|α|=0.604,λD ≈2.86,the black circle corresponds to λ=4.113,Δc=-0.6,|α|=0.607,λD ≈4.86,and the blue cross corresponds to λ=5.069,Δc=-2 ,|α|=0.608,λD ≈6.08 for κ=1.2,U=6,UD ≈2.21 .The IPR of different eigenstates as a function of energies for (b) the green square,(c) the black circle,and (d) the blue cross.Here,K=0.8,and L=1974.

为了考察实际的腔场参数与重返局域化现象的关系,在图8(a)中选取3 种不同的点去计算它们的IPR,通过数值计算可以得到此时图8(a)中绿色方块、黑色圆圈、蓝色叉号处所对应的|α|分别为 0.604,0.607 和 0.608,λD分别 为 2.86,4.86 和6.08,且具有相同的UD≈2.21 .为了进一步验证此时这3 个点所对应的局域化性质,图8(b)—(d)分别给出了它们的IPR 随着全部能量的变化情况.可以看出|α|=0.604,λD≈2.86 时,系统已经处于完全局域相.而在|α|=0.607,λD≈4.86 时,部分态处于局域态,部分态处于扩展态,系统处于临界相.最后,在|α|=0.608,λD≈6.08 时,所有态又重新回到局域态.由此可见,通过合理地调节腔场的参数,在超辐射相区可以实现重返局域化现象.

之前讨论了K=0.8 时的情况,图9 分别给出了K=0.5 和K=1.5 时,超辐射相变与局域化相图的情况.可以看出,当K的取值在有限的变化范围内(以K=0.5 (图9(a1))和K=1.5 (图9(b1))为例),对于不同的腔场耦合强度U,光场|α|随泵浦和腔的耦合强度λ的变化具有类似的转变行为.对于不同的K值,如图9(a2)和图9(b2)所示的K=0.5和K=1.5 情况,展示了与前文中K=0.8 类似的局域化相图.由此可见,当K取值与J处于相同量级时,系统展示了类似的超辐射和局域化相变.

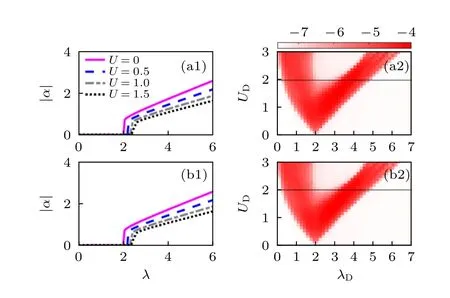
图9 (a1) K=0.5,(b1) K=1.5时,腔场耦合强度U取不同的值时,光场 |α| 随着耦合强度λ 变化的图像.这里,L=1974 ,β=610/987 ,Δc=-2 和 κ=1.2 .(a2) K=0.5,(b2) K=1.5 时,λD-UD 参数平面内,以序参 量η 的大小为填充颜色的相图,其中白色区域表示完全扩展或局域相,红色区域表示具有迁移率边的临界相.这里,L=1974Fig.9.The cavity field |α| as a function of the pumping strength λ for different U for (a1) K=0.5,(b1) K=1.5 .Here L=1974 ,β=610/987,Δc=-2 and κ=1.2 .Phase diagram in the λD-UD plane with L=1974 for(a2) K=0.5,(b2) K=1.5 .The color code represents the values of η,where the white regions denote the full extended or localized phase and the red region represents the critical phase.

4 结论

本文研究了在高精度光腔中由超辐射引起的准周期调制的梯子模型.通过数值计算发现系统中存在迁移率边以及重返局域化现象,并且得到了全参数空间的相图.在本文研究的调制强度UD范围内,系统的相图被临界值分为两部分,在小于临界值的区间,系统随着λD的增大,仅仅出现一次具有迁移率边的临界相;而在大于临界值的部分,系统随着λD的增大,会出现重返局域化现象.

重返局域化现象最初是在具有奇偶交错的准周期调制的Su-Schrieffer-Hegger (SSH) 模型中发现的[24],并且重返局域化现象出现的区间非常狭小,这给实验探测带来了极大的挑战.而对于最初的理论方案中如果选取一个无奇偶交替的准周期调制时,此一维晶格并不会出现重返局域化现象,仅仅能观测到迁移率边的存在.本文提出了一种梯子形冷原子体系与光腔耦合的方案,此方案并不要求奇偶交替的调制并且具有有限的重返局域化相区.以碱金属原子23Na 为例实现该理论模型,其中钠原子被捕陷在一个晶格长度约为 266 nm 的梯子形光晶格中,其晶格隧穿强度约为 2π×200 kHz,并且选用腔长约为 300µm—1 mm,耗散率κ约为2π×240kHz 的高精度腔,泵浦光的频率与腔场频率相差Δc≈2π×140—2π×600 kHz.通过调节腔场和泵浦场各个参数,实现耦合强度λ和腔及原子的耦合强度U达到 2π×800 kHz,这些参数是目前实验上可实现的.值得注意的是,在平均场近似下,当超辐射相变发生时,梯子模型将出现两种不同频率的调制,而这两种不同频率的准周期调制的共同作用是出现重返局域化的主要原因.本文所研究的重返局域化现象的出现并不依赖于所填充的原子种类.但是由于费米子体系存在泡利不相容原理,造成发生超辐射相变的难易程度与原子填充数有关[28-32],使得计算过程更为复杂.本文为了理论计算的简便仅关注了玻色原子的情况.该工作为原子与光腔耦合系统和重返局域化现象的研究建立了联系,也为重返局域化的研究提供了新的思路.