基于系数搜索的振动补偿方法*
要佳敏 庄伟 冯金扬 王启宇 赵阳 王少凯 吴书清 李天初
(中国计量科学研究院,北京 100029)
1 引言
绝对重力测量,即对重力加速度绝对值的精确测量,在辅助导航、资源勘探、地球物理、计量领域都有着广泛的应用[1-4].现有的高精度绝对重力仪普遍采用自由落体法,主要包括以角锥棱镜为下落物体的激光干涉式绝对重力仪[5-8]和以冷原子团为下落物体的原子干涉式绝对重力仪[9-14],以下分别简称为光学重力仪和原子重力仪.前者通过激光干涉仪测量角锥棱镜在真空中自由下落的运动轨迹,拟合求解重力加速度,后者根据原子团在自由下落的过程中经过3 次拉曼激光脉冲作用形成的原子干涉条纹来计算重力加速度.由于二者的实际测量对象是下落物体或下落原子团相对于仪器内一个参考镜(角锥棱镜或平面镜)的运动加速度,因此参考镜自身的加速度必然耦合到测量结果中.理论上,忽略参考镜自身振动时,现有的绝对重力仪的测量精度可以达到微伽(µGal,1 µGal=1 ×10—8m·s—2)量级;但实际上,如果直接将参考镜放置在地面上,地面振动引起的测值离散度将超过10 µGal,在复杂振动环境中甚至达到mGal 或10 mGal 量级.因此,利用测振仪器获得参考镜自身的运动加速度并在计算重力加速度时对其影响进行修正是提高绝对重力仪测量精度的有效手段之一,这种修正方法一般称为振动补偿.
具体而言,影响原子重力仪的地面振动噪声主要为环境噪声,与测量时间和测量点的地基、坐标及环境有关,可以根据频率来粗略区分.首先是人类活动噪声,一般大于1 Hz,如仪器测试期间附近的人员走动,车辆等人工振源产生的振动,以及建筑物的晃动等.其次是来自地球本身的噪声,一般在0.1—1.0 Hz 之间,主要包括周期性的脉动和地震等地球内部运动引起的振动,其中地脉动噪声模型的加速度功率谱密度在频率为0.2 Hz 和3.0 Hz的位置存在峰值[15].最后是气压波动等大气运动噪声,一般小于0.1 Hz,普遍变化缓慢且幅值较低,对绝对重力测量的影响可以忽略[16,17].由于绝对重力测量只依靠垂直方向的位移数据进行计算,因此对原子干涉条纹进行振动补偿时,一般忽略地面振动的水平分量,仅需使用测振仪器输出的垂直振动信号.
目前国际上较为成熟的原子重力仪是法国巴黎天文台研制的CAG-01 型原子重力仪,曾参加过多次国际重力比对,采用的振动处理方法为被动式垂直隔振系统与振动补偿的结合,其中振动补偿的具体原理为:数据采集卡同步记录原子干涉过程中的地震计输出的速度信号与原子干涉条纹,在控制软件中利用无限冲激响应(infinite impulse response,IIR)滤波器和非因果低通滤波器对地震计信号进行处理,以减小地震计传递函数幅频特性不恒定、相频特性存在非线性的影响,获得更真实的参考镜振动信号,最后利用处理后的信号得到由参考镜振动引入的相位噪声,修正原子干涉条纹.在该仪器所在的测量环境中,此振动补偿方法本身可以使重力仪灵敏度提升为原来的3 倍[11].德国汉诺威大学提出利用数字式低通和高通滤波器对振动传感器的输出信号进行前处理,以得到更为精确的参考镜振动引入的相位噪声,从而实现振动补偿.其实验结果表明,在较安静的环境中利用高精度商用地震计进行振动补偿,或在复杂振动环境中使用精度较低的商用加速度计或其自主研制的新型光学惯性传感器进行补偿,均可以有效提高重力仪的灵敏度[18].在我国,浙江大学自制的原子重力仪同样采用了振动补偿方法,其主要特点为利用商用反演软件修正地震计实测传递函数的影响以获得更真实的参考镜振动信号.在其实验室环境中,该方法可以将重力仪的灵敏度提升至与使用被动隔振系统时相近的水平[19].国防科技大学对参考镜垂向振动及水平偏转引入的测量噪声进行了详细分析,利用加速度计测量原子重力仪工作时的参考镜振动,同时对加速度计与参考镜之间的传递函数进行了较为精确的标定.实测结果表明在较复杂的振动环境中其振动补偿方法可以实现显著的振动补偿效果[20].军事科学院国防创新院提出的振动补偿方法则采用具有高精度四通道移相探测器的迈克耳孙激光干涉仪替代传统振动传感器.该干涉仪可以直接测量出原子干涉条纹的相移,并结合信号整形、数字鉴相等方法确定拉曼激光脉冲作用前后原子干涉条纹的相位小数的变化,得到参考镜振动引起的原子干涉相位偏差.去除该相位偏差,即可对重力仪测量到的跃迁概率信号进行修正[21].此外,中国计量科学研究院、中国科学院精密测量研究院、华中科技大学、中国科技大学、国防科技大学、美国斯坦福大学、德国洪堡大学等单位也研制了不同类型的隔振系统[12,13,22-26],以减小地面振动对原子重力仪的影响.
德国汉诺威大学的Richardson 等[18]和我国国防科技大学的研究人员[20]均指出,传统振动传感器与参考镜由于安装位置不同形成的机械传递函数可能是影响振动补偿精度的重要因素;在原子重力仪进行正式测量前对该传递函数中的关键系数进行初始标定有助于提高振动补偿效果.这些分析为提升原子重力仪的振动补偿精度提供了重要指导,但目前尚无具有普适性的、能够在任意测量时间及地点快速实现对传递函数进行实时修正的具体振动补偿算法.而在光学重力仪方面,清华大学的研究人员给出了对重力测量结果进行实时修正的基于相同简化模型的具体振动补偿算法,并提供了该算法在不同地点对延时系数和增益系数进行实时计算的结果及重力测量的实测结果[27-29].他们采用的传感器为高精度地震计,利用相关分析法或黄金分割法搜索出当前环境下这2 个系数的具体值,并对下落物体轨迹信号进行修正.对同一套振动补偿算法,输入在中国计量科学研究院昌平院区的安静环境中测得的重力数据和地震计数据,算法的直接输出结果表明振动补偿后光学重力仪的测量分辨率可以提升5 倍;输入在清华大学所处的复杂振动环境中的数据,结果表明振动补偿可将重力仪的测量分辨率提升16 倍,效果更为显著[27].该算法最大的特点是较强的自适应性,在不同时刻和不同地点的测量过程中可以直接使用,以保证真实的机械传递函数因环境变化而发生改变时对其当前值进行实时估算,实现当时当地最好的振动补偿效果.受上述研究结果的启发,基于上述简化模型,本文给出了一套振动补偿算法的工作原理和具体流程,该振动补偿算法可以应用于原子重力仪,对传递函数进行实时标定.我们通过仿真运算对算法的有效性进行了详细验证,最后利用实验室自主研制的原子重力仪实际评估了该算法对原子干涉条纹拟合精度和重力测值离散度的补偿效果,为提高原子重力仪在不同环境甚至是复杂振动环境中的测量精度提供帮助.
2 原 理
2.1 应用于原子重力仪的振动补偿原理
原子重力仪基于冷原子物质波干涉原理,将激光脉冲作用到冷原子团,通过双光子受激拉曼跃迁或多光子布拉格衍射过程来实现原子干涉过程[9].以基于受激拉曼跃迁的原子重力仪为例,冷原子团在真空腔中自由下落,真空腔下方的平面参考镜将垂直向下的拉曼激光原路反射,使两束对射的激光同时作用于原子团,在此过程中3 个连续的激光脉冲实现了原子波包的分束、反转和合束,分别为第1 个π/2 脉冲、π 脉冲和第2 个π/2 脉冲,相邻脉冲的时间间隔为T[30].合束后任一能态的原子均由2 条路径上的原子叠加而成,通过荧光信号可以探测脉冲作用后原子团的跃迁概率P,即干涉条纹,满足

式中:ΔФ为原子相位,与当地的重力加速度g有关;代表条纹对比度的系数A和B可以通过对干涉条纹进行余弦拟合得到.理想情况下,原子相位ΔФ等于其理论值ΔФth,即
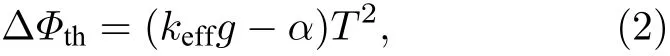
式中,keff为有效波矢,α表示激光的扫频速率.重力仪的控制软件调控 (2) 式中的α线性增大,则原子相位ΔФ也将线性变化,使干涉条纹呈现为标准余弦信号的形式.此时P应与由P拟合出的标准信号Pfit完全相同,有

但实际情况下,受到各种相位噪声的影响,原子相位ΔФ等于其实际值ΔФm,有
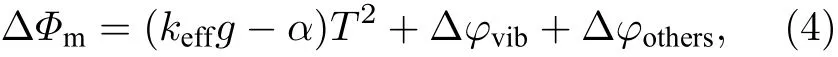
式中Δφvib为参考镜振动引入的相位噪声,以下简称为振动相位;Δφothers为其他噪声源引入的相位噪声的总和,以下简称为其他相位噪声.此时P由Pfit变为
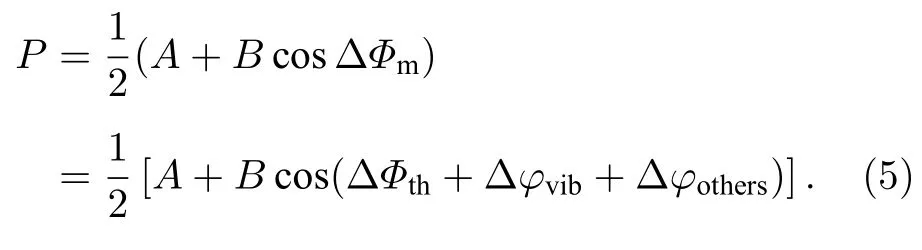
当振动相位在相位噪声中占主导时,依据上述原理可以确定修正干涉条纹P的振动补偿过程.第一步,对原始实测条纹P(ΔФth)进行余弦拟合,得到拟合出的理论条纹Pfit(ΔФth)和(1)式中的系数A和B.需要说明的是,此时可以将原子重力仪在正式测量前的初始测量过程中获得的粗测值gth代入(2)式以得到拟合条纹Pfit.这是因为原子重力仪到达一个新的测量地点后一般都需要在启动阶段通过改变拉曼间隔T并扫描扫频速率α来获得正式测量所用的中心值αcenter,而该测点的粗测重力值即为gth=αcenter/keff.此后每一次或每一组跃迁概率数据都对应真实重力值相对于该粗测值的偏差Δg,所以实际上重力仪最终输出的高精度测值为g=gth+Δg.因此利用粗测值gth计算拟合条纹有利于提高计算效率,这也符合原子重力仪的一般测试流程[19,20].第二步,通过振动传感器获得一段时间t内参考镜的真实振动速度vm(t),进而根据
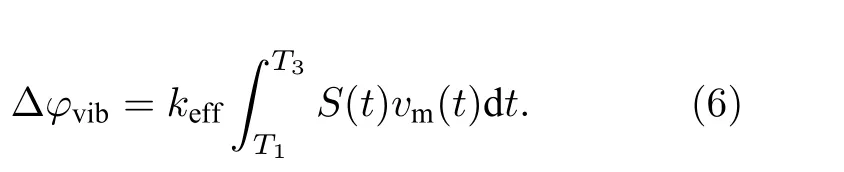
计算出真实的振动相位Δφvib,其中S(t)为重力仪的灵敏度函数,T1和T3分别为第1 个π/2 脉冲和第2 个π/2 脉冲的作用时刻,均由重力仪控制软件的已知参数决定.第三步,计算出仅受振动影响时的原子相位ΔФv和跃迁概率Pv,即
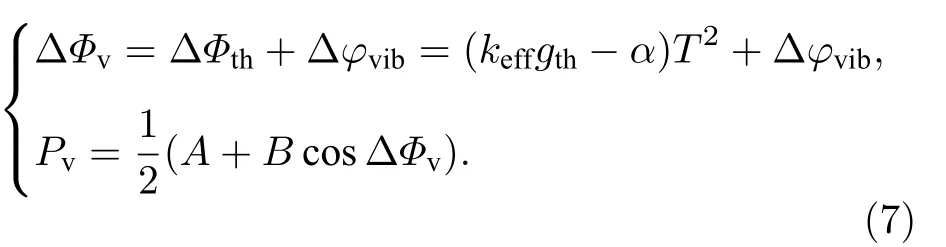
此时重新以ΔФv为横坐标、P为纵坐标得到的数据对P(ΔФv)即为修正后的干涉条纹,至此补偿过程结束.如图1 所示,与蓝色圆圈表示的原始条纹P(ΔФth)相比,红色方块表示的修正条纹P(ΔФv)的横坐标有所移动,理论上应更接近灰色的标准余弦信号,即拟合出的理论条纹Pfit(ΔФth).也就是说,对修正后的条纹P(ΔФv)再次进行余弦拟合时的均方根误差(root mean square error,RMSE)值应小于对原始条纹P(ΔФth)进行拟合时的RMSE 值.

图1 原子干涉条纹示意图Fig.1.Schematic diagram of the fringe signal of atomic interferometer.
2.2 基于传递函数简化模型的振动补偿方法
基于传递函数简化模型以实现上述振动补偿过程的方法包括硬件和软件两方面.
硬件方面,由于目前尚无以原子重力仪的参考镜为敏感质量的地震计,因此一般而言只能用一台独立的地震计或加速度计放在参考镜旁边或下方测量其振动.然而,受机械结构及地震计自身性能的限制,地震计输出信号Us(t)并不能完全真实地反映参考镜的振动速度vm(t),二者的关系如图2所示,其中Ga表示从地面振动速度到参考镜振动速度的传递函数,Gb表示从地面振动速度到地震计敏感质量振动速度的传递函数,Gc表示从敏感质量运动速度到地震计输出电压之间的传递函数.由于地震计内部的敏感质量与参考镜的实际位置必然存在水平和垂直差异,因此Ga与Gb不可能相等,且当地基材料改变时,这两个传递函数本身也可能发生变化.另一方面,地震计自身的传递函数Gc并非幅频特性恒定、相频特性为线性的理想传递函数[31],且有可能随测量时间与环境的改变而发生变化(这是因为温度、湿度、气压等环境参数会对地震计内部的机电模块参数产生影响,且这些参数可能随时间发生漂移).综上,参考镜的真实振动速度与地震计输出的电压信号之间的传递函数H满足
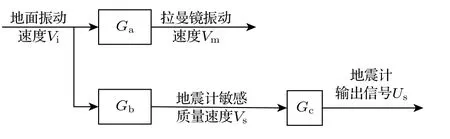
图2 地震计输出信号与参考镜真实振动的关系Fig.2.Transfer function between the vibration of reference mirror and the output signal of seismometer.
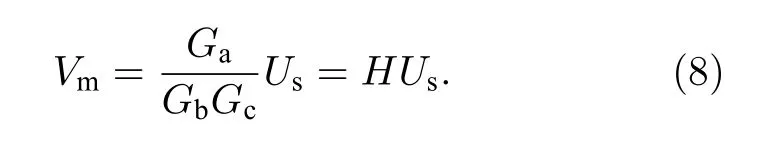
因此对传递函数H的求解将直接影响振动补偿的效果.
虽然实际情况中Ga,Gb,Gc不易测量且可能改变,导致测量人员无法得到总传递函数H的精确值,但由于单次重力测量任务中测量环境不会有显著变化,且测量时间一般不超过24 h,因此可以利用由一个延时系数τ和一个增益系数K组成的简化模型来估算H,并认为这两个系数的数值在当前测量过程中保持不变[27].由此可得图2 的简化模型为
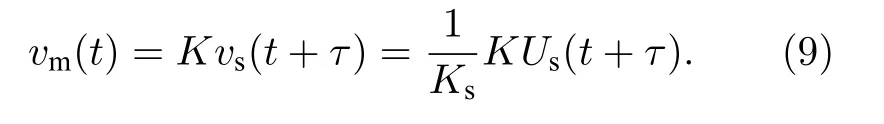
式中,Ks为地震计的标称灵敏度,由制造商提供.
理论上当延时系数τ和增益系数K取最接近真实值时,利用地震计输出电压Us和(9)式计算出的参考镜振动速度vm(t)也最接近真实值,对条纹的修正效果最好.因此振动补偿可以选取对条纹进行拟合时的RMSE 值作为优化目标,基本思路为:给定τ的取值范围,遍历搜索使RMSE 值达到最小值时对应的最优延时系数τopt;再给定K的取值范围,在设定延时为τopt的情况下,再次遍历搜索使RMSE 达到最小值时对应的最优增益系数Kopt.最后,在设定延时为τopt、增益为Kopt的情况下,得到修正后的条纹P(ΔФv)及其余弦拟合时的RMSE 值.
由此得到具体的算法流程如图3 所示,相应的处理程序即为振动补偿方法的软件部分.上述分析中使用的主要物理符号汇总在表1 中.

表1 主要物理符号描述Table 1.Description of main symbols.

图3 基于系数搜索的振动补偿算法流程Fig.3.The algorithm of the vibration correction method based on element searching.
2.3 振动补偿前后干涉条纹拟合残差的变化
上述振动补偿算法的优化目标为拟合干涉条纹时的RMSE 值.该值具有简单直观的数学含义,但物理意义不明显.类比基于相同简化模型的振动补偿方法在光学重力仪中的算法流程[27],可以用另一种更具有物理意义的变量作为振动补偿效果的最终评价指标,即干涉条纹拟合残差的变化.
运行振动补偿算法前,先计算出原始条纹P(ΔФth)相较于理论条纹Pfit(ΔФth)的残差Rm(ΔФth)的标准差σm,即

运行振动补偿算法后,利用搜索出的最优延时系数τopt和增益系数Kopt,根据(6)式,(7)式和(9)式得到仅受振动影响的干涉条纹Pv相较于理论条纹Pfit的残差Rv.同时,记原始条纹P与仅受振动影响的条纹Pv的差值为Rc.显然Rc也就是原始条纹残差Rm与仅受振动影响的条纹残差Rv的差值,相当于去除振动影响后的条纹残差.理论上振动补偿效果越好,则振动相位Δφvib的计算越准确,推算出的仅由振动引入的条纹残差Rv也越接近原始条纹残差Rm.此时Rc将趋近于仅由其他相位噪声Δφothers引入的条纹残差,其标准差σc也应趋于最小值.因此可以以

相较原始条纹残差Rm的标准差σm的衰减程度作为衡量振动补偿效果的最终指标.
3 仿真验证
上述振动补偿算法的效果将在实验室自主研发的NIM-AGRb-1 型原子重力仪[12]上进行考察.实际测量之前,可以利用美国 MathWorks 公司生产的 MATLAB 软件验证算法的有效性,具体的仿真流程为:1) 参考NIM-AGRb-1 型重力仪的控制参数和之前的实测数据,给定合理的计算参数值,包括波矢keff、粗测重力值gth、灵敏度函数S(t)、拉曼激光的脉冲间隔T=80 ms、1 min 内线性增大的扫频速率序列α(时间间隔为2 s,相当于原子团的下落间隔)、决定干涉条纹对比度的系数A和B等;2) 给定1 min 内代表随机振动的速度信号的幅值Arand和代表地脉动的速度信号的频率序列fs及相应的幅值序列As,具体取值参考地脉动噪声功率谱密度的新高噪声模型 (new high noise model,NHNM)[15],设定参考镜真实振动速度信号vm(t)为这些信号的总和;3) 根据(6)式计算参考镜振动引入的真实相位噪声Δφvib,再根据(4)式和(5)式计算其他相位噪声Δφothers为0 时的跃迁概率Psim,该概率Psim即代表原子重力仪输出信号P的仿真值,数据量N=30,如图4(a)所示;4)设定真实延时系数τset=5 ms,真实增益系数Kset=0.9,设定地震计灵敏度Ks为将在实测中使用的CMG-3 ESP 型地震计的灵敏度,根据(9)式反推出此时地震计敏感质量的振动速度和地震计输出电压的仿真值vs(t)和Us(t),注意Us(t)即代表地震计在原子重力仪工作时同步输出的信号,如图4(b)所示;5)对上述仿真出的概率Psim和地震计电压信号Us(t)运行振动补偿算法.

图4 (a) 仿真干涉条纹;(b) 仿真振动信号Fig.4.(a) The simulated fringe signal;(b) the simulated output of seismometer.
记以上仿真过程为第1 种情况,运算结果如图5 和图6 所示.可以看出,不考虑其他相位噪声时,该算法可以精确地搜索出设定的延时系数τ=5 ms 和增益系数K=0.9(如图中黑色虚线所示,下同),并将原始条纹Psim(ΔФth)调整为更接近理论条纹Pfit(ΔФth)的修正条纹Psim(ΔФv),其中典型的修正位置用橘色圆圈标出.补偿前对原始条纹Psim(ΔФth)进行余弦拟合时的RMSE 值为13.1×10—3,而补偿后对修正条纹Psim(ΔФv)进行余弦拟合时的RMSE 值仅为0.02×10—3.同时该算法计算出的仅受振动影响的条纹相对于理论条纹的残差Rv(ΔФth)和原始条纹相对于理论条纹的残差Rm(ΔФth)完全相同.依据2.3 节提出的评价指标,此时原始条纹残差Rm的标准差σm为12.39×10—3,而去除振动影响后的条纹残差Rc的标准差σc仅为0.02×10—3,衰减幅度达到99.8%,验证了该振动补偿算法的有效性.
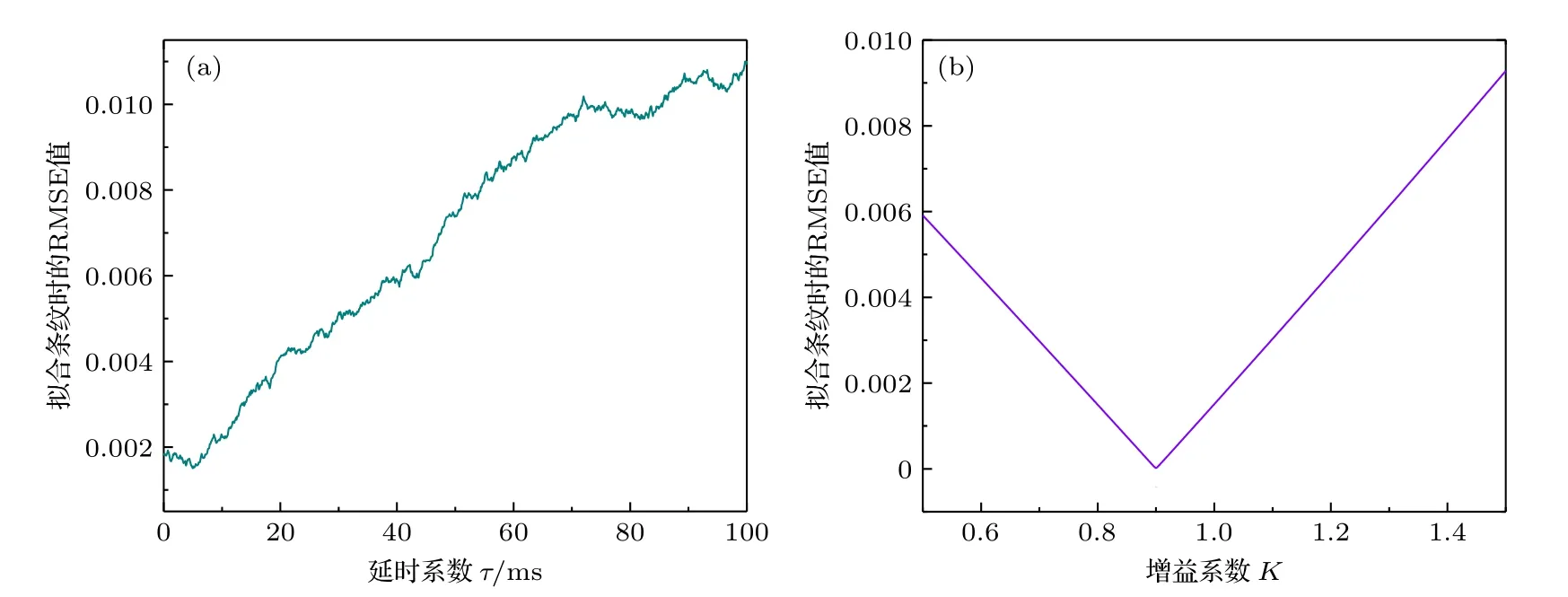
图5 其他相位噪声为0 时仿真得到的拟合RMSE 值与(a)延时系数和(b)增益系数的关系Fig.5.The RMSE value of fringe fitting as a function of (a) time delay and (b) proportional element,without considering other phase noises,calculated by simulation.

图6 其他相位噪声为0 时仿真得到的(a)修正前后的干涉条纹与理论拟合曲线(典型修正点用橘色圆圈标出),(b)原始条纹的拟合残差与计算出的仅由振动导致的条纹的拟合残差Fig.6.(a) The simulated fringe signals before and after vibration correction with the fitted curve as the reference (with the typical corrected data marked by orange circles),and (b) the fitting residual of the simulated fringe signals,without considering other phase noises.
进一步,修改前述仿真流程的第3 步,设定其他相位噪声Δφothers为±10 mrad 范围内的随机值.这种设定可以更准确地模拟实际测量,记该仿真过程为第2 种情况.此时虽然振动相位Δφvib的范围约为±400 mrad,是其他相位噪声Δφothers的40 倍,但仿真运算结果表明其他相位噪声的干扰仍不可忽视.如图7 和图8 所示,此时算法搜索出的延时系数为τ=2.7 ms,与设定值的区别达到毫秒量级;增益系数为K=0.957,与设定值相比偏大6.3%.此时虽然该算法同样可以将原始条纹Psim(ΔФth)调整为更接近理论条纹Pfit(ΔФth)的修正条纹Psim(ΔФv)(典型位置如橘色圆圈所示),但偶尔会因设定为随机值的其他相位噪声Δφothers而产生随机运算误差,如绿色方框所示的数据被修正到理论条纹曲线的另一侧而不是曲线上;计算出的仅由振动引入的条纹残差Rv(ΔФth)和原始条纹残差Rm(ΔФth)大致相同,但也存在一定差异.最后,此时原始条纹残差Rm的标准差σm为17.32×10—3,而去除振动影响后的条纹残差Rc的标准差σc为7.82×10—3,衰减幅度为54.8%,明显小于第1 种情况的衰减幅度.
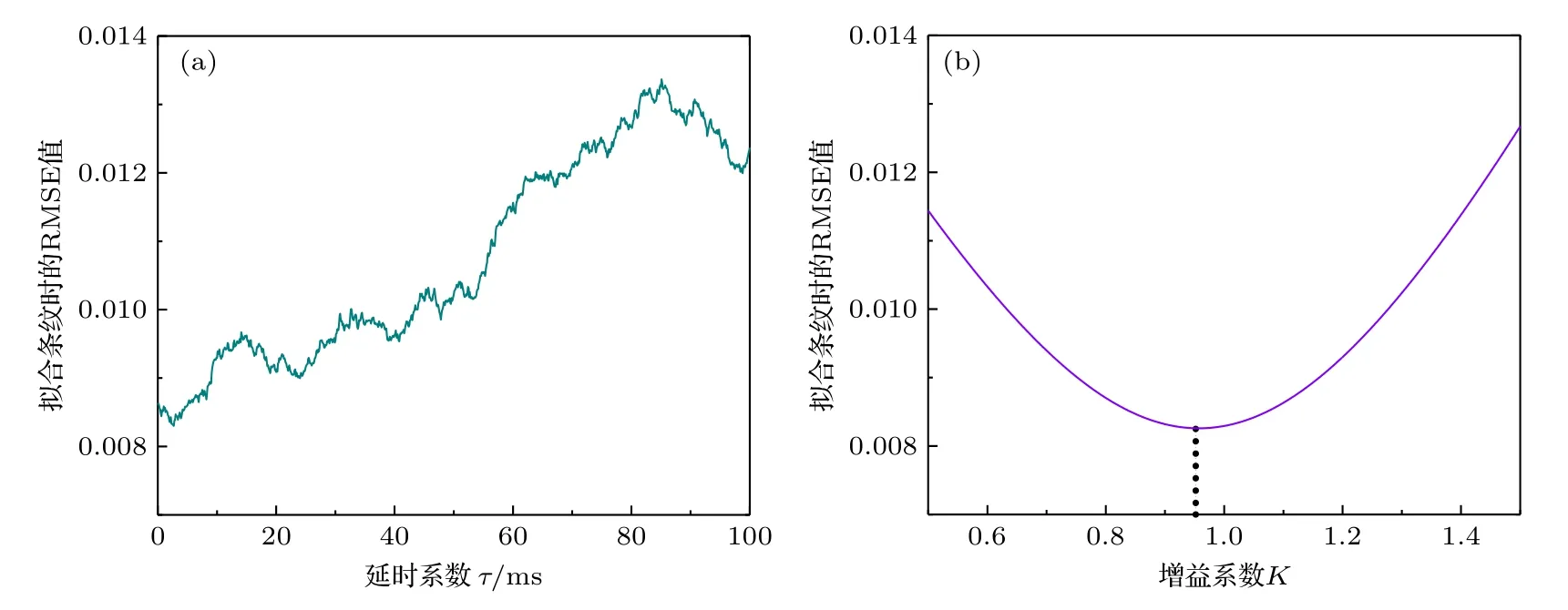
图7 考虑其他相位噪声时仿真得到的拟合RMSE 值与(a)延时系数和(b)增益系数的关系Fig.7.The RMSE value of fringe fitting as a function of (a) time delay and (b) proportional element,with other phase noises considered,calculated by simulation.
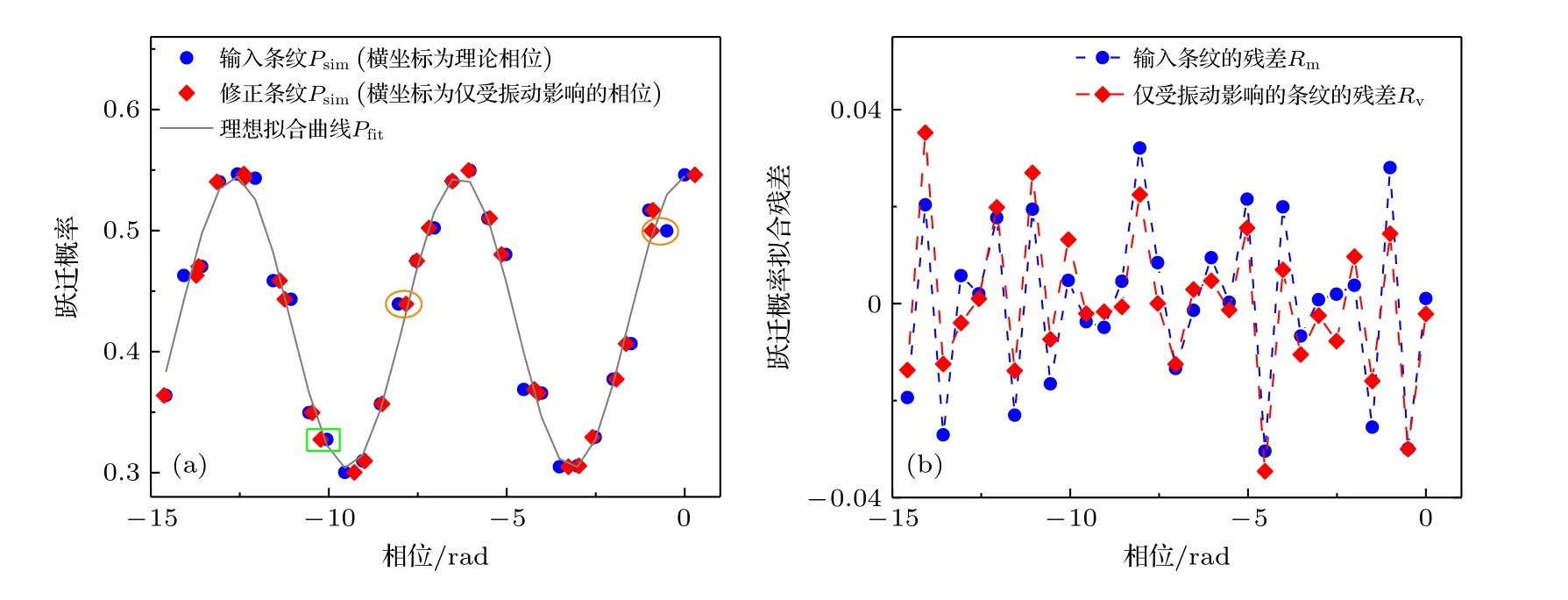
图8 考虑其他相位噪声时仿真得到的(a)修正前后的干涉条纹与理论拟合曲线(典型修正点用橘色圆圈和绿色方框标出),(b)原始残差与计算出的仅由振动导致的条纹残差Fig.8.(a) The simulated fringe signals before and after vibration correction with the fitted curve as the reference (with the typical corrected data marked by orange circles and green square),and (b) the fitting residual of the simulated fringe signals,with other phase noises considered.
上述结果说明其他相位噪声将明显限制振动补偿算法的有效性.当振动环境变差,即振动相位Δφvib在总相位噪声中的权重增加时,算法的有效性将显著提升.例如,仍取其他相位噪声Δφothers为±10 mrad 范围内的随机值,将参考镜振动信号vm(t)中随机振动的幅值Arand增大为原来的10 倍,并记该仿真过程为第3 种情况.此时拟合得到的延时系数为τ=4.1 ms,增益系数为K=0.919,比第2 种情况更接近设定值;原始条纹残差Rm的标准差σm为29.28×10—3,去除振动影响后的条纹残差Rc的标准差σc为6.78×10—3,衰减幅度为76.8%,高于第2 种情况.因此,理论上当原子重力仪在复杂振动环境中测量时,该算法将发挥更为明显的作用.
另一方面,增大数据量可以在小范围内提升振动补偿算法对延时系数和增益系数的计算精度,但对条纹修正效果的提升水平有限.例如,设定其他相位噪声Δφothers和振动相位Δφvib取值等同于第2 种情况,但将原子团下落的时间间隔减小为1 s.在仿真总时长仍为1 min 的情况下,此时跃迁概率信号的数据量扩大1 倍,达到N=60,记该仿真过程为第4 种情况.此时拟合得到的延时系数为τ=6.8 ms,增益系数为K=0.876,比第2 种情况更接近设定值;但原始条纹残差Rm的标准差σm为14.80×10—3,去除振动影响后的条纹残差Rc的标准差σc为6.56×10—3,衰减幅度为55.7%,和第2 种情况差别不大.
表2 汇总了以上所有运算结果.可以看出,补偿前后对条纹进行余弦拟合时的RMSE 值的衰减幅度和条纹残差标准差的衰减幅度及变化规律大致相同.如2.3 节所述,条纹残差的变化更具有物理意义,因此在后续分析实测结果时不再专门提及RMSE 值的衰减幅度.

表2 仿真运算结果Table 2.Simulated results.
4 实验结果
4.1 实验设备
该振动补偿算法的实际效果在中国计量科学研究院自主研制的NIM-AGRb-1 型原子重力仪上进行了验证.NIM-AGRb-1 型重力仪具有两种工作模式:其一为条纹扫描模式,在此期间拉曼激光波矢keff保持不变,扫频速率α线性增加,可以得到原子干涉条纹;其二为重力测量模式,在此期间拉曼激光波矢keff不断反向,即每一次作用于下落原子团时,激光脉冲的波矢keff均与上一次作用时数值相同、方向相反.此时,结合在原子钟上运用的闭环锁相技术,可以实现对扫频速率α的交叉锁定,进而保证每一次原子团下落后都能得到重力测值g,而不必等待整个干涉条纹测量完毕后拟合出初相位进而计算出重力值,或依据基于不同拉曼间隔T得到的干涉条纹的交叉点位置来计算重力值.配合清华大学研制的被动式零长弹簧结构的隔振系统,该重力仪可实现44 µGal·Hz—1/2的灵敏度,合成不确定度约为5.2 µGal[12].
验证该振动补偿算法时,NIM-AGRb-1 型重力仪在第一种条纹扫描模式下工作,此时重力仪的输出信号为实测跃迁概率P而非重力测值g,且最多扫描3 个整周期的干涉条纹.本实验的现场情况如图9(a)所示,测试地点为中国计量科学研究院昌平院区的重力实验楼.实验过程中参考镜直接放置在重力仪探测腔下方的地面上,旁边放置英国Guralp 公司生产的CMG-3 ESP 型地震计,其输出信号的灵敏度为Ks=2000 V·m—1·s[31].探测腔中冷原子团下落期间的激光脉冲的时间间隔为T=80 ms,激光波长约为780 nm,相邻原子团下落的时间间隔为2 s.受重力仪自身软件的控制,采集跃迁概率P的数据采集卡的采样频率为1 Hz,无法用于对地震计输出电压的采样,因此使用第二台美国National Instruments 公司生产的PXIe-6361 数据采集卡[32]来记录地震计的输出信号Us(t),采样频率为500 kS/s,如图9(b)所示.该采集卡还同步采集了重力仪的某一路触发信号Utrg(t).重力仪的控制软件控制采集该信号总比原子团下落时的第1 个π/2 脉冲提前40 ms,从而确保两台采集卡分别采样的数据可以在时间上互相匹配.

图9 实验现场图 (a) NIM-AGRb-1 型原子重力仪;(b)地震计信号及触发信号采集系统Fig.9.Photograph of (a) NIM-AGRb-1 atomic-interferometry absolute gravimeter,and (b) the data acquisition device recording the voltage signal of seismometer and trigger.
该测试地点位于地广人稀的郊区,周围无交通、建筑和大型机械振源,且具有隔振地基,属于非常安静的测试环境,其地面振动加速度的功率谱密度如图10 所示.由于NIM-AGRb-1 型重力仪体积较大,尚无法搬运至其他地点,因此本次实验暂且仅在该安静环境中进行.之后该算法的振动补偿效果也将在振动条件更为复杂的环境中验证.
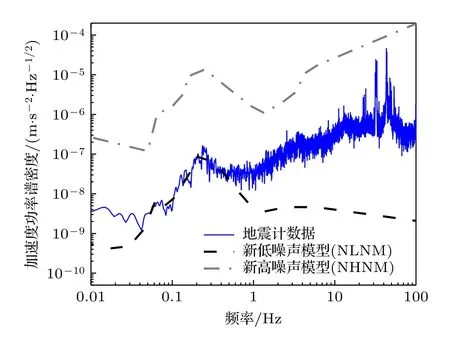
图10 测试地点的地面振动加速度功率谱密度Fig.10.The power spectrum density of the ground vibration acceleration at the measurement site.
4.2 实验结果
本次实验首先采集了10 组数据,每组数据包含30 次原子团下落过程,其他控制参数如前所述.对每组数据分别运行振动补偿算法,结果如表3 所示.

表3 10 组数据的实际测量结果Table 3.Measurement results obtained from 10 data sets.
可以看出该振动补偿算法在安静环境中已具有良好的条纹修正效果,去除振动影响后的条纹残差Rc的标准差σc相比原始条纹残差Rm的标准差σm的衰减幅度的均值达到44.4%,最大可达58.2%,与表1 中第2 种仿真情况的运算结果基本一致;相比对原始条纹进行余弦拟合时的RMSE值,拟合修正条纹时的RMSE 值也显著减小.另一方面,各组数据分别计算出的最优增益系数Kopt的标准差为0.115(均值为1.119),计算误差较小;而最优延时系数τopt的标准差为2.47 ms(均值为3.56 ms),计算误差较大.前述表2 中第2 种情况的仿真结果已说明,即使Δφothers比Δφvib小1 个量级,τopt的计算误差也将达到毫秒量级.因此最有可能导致实测结果中τopt的标准差达到毫秒量级的原因仍是其他相位噪声Δφothers.这再次说明在后续工作中有必要在复杂振动环境中验证该算法的振动补偿效果,即考察振动相位Δφothers在总相位噪声中所占的权重更大时,σc相比σm的衰减幅度以及延时系数和增益系数的计算精度能否如仿真预测一样提升.
可以以第1 组数据的计算结果为例观察振动补偿算法的工作过程.如图11 所示,该算法可以有效搜索出拟合条纹的RMSE 达到最小值时对应的唯一最优延时系数τopt和最优增益系数Kopt.从图12(a)可以看出,相比原始条纹P(ΔФth),对横坐标进行振动补偿后的修正条纹P(ΔФv)更接近理论条纹Pfit(ΔФth)(典型位置如橘色圆圈所示).补偿前对原始条纹P(ΔФth)进行余弦拟合时的RMSE 值为11.2 × 10—3,而补偿后对修正条纹Psim(ΔФv)进行余弦拟合时的RMSE 值减小为4.8 × 10—3.原始条纹P相对于理论条纹的残差Rm(ΔФth)和从地震计实测信号推算出的仅受振动影响时的条纹Pv相对于理论条纹的残差Rv(ΔФth)也基本吻合,如图12(b)所示.
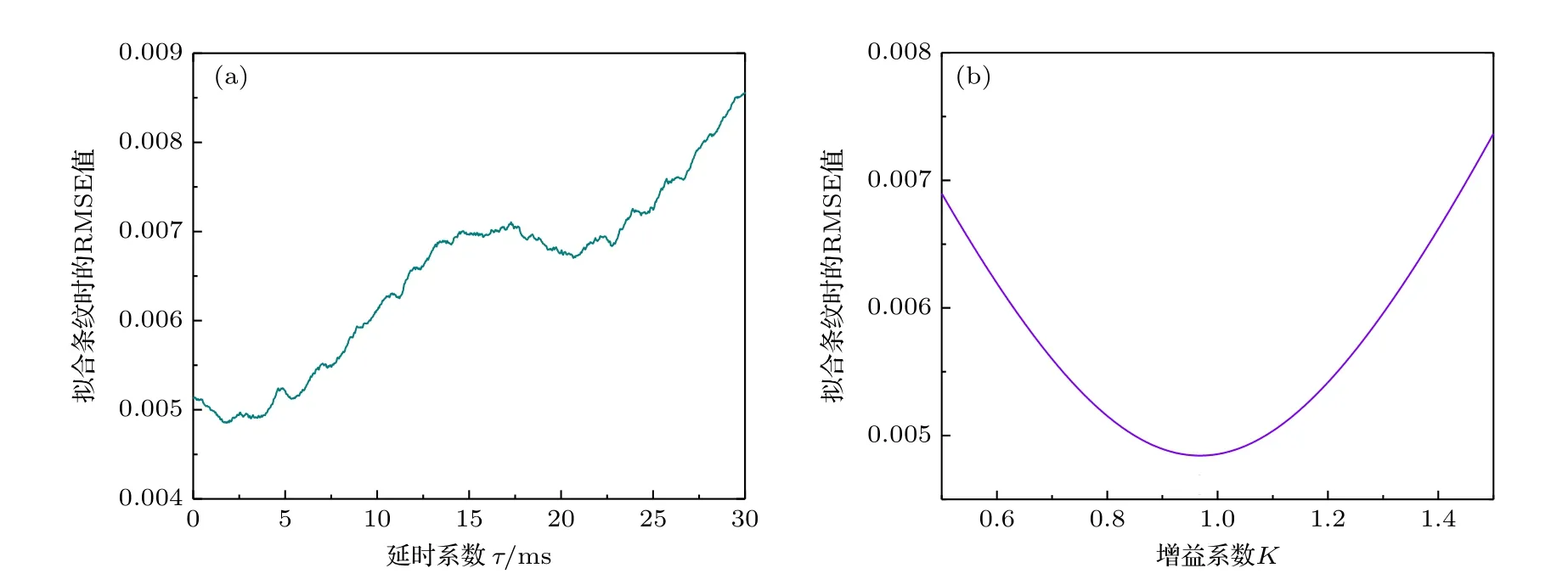
图11 第1 组实测数据的拟合RMSE 值与(a)延时系数和(b)增益系数的关系Fig.11.The RMSE value of fringe fitting as a function of (a) time delay and (b) proportional element,calculated from the 1st dataset of measurement.

图12 第1 组实测数据(a)修正前后的干涉条纹与理论拟合曲线(典型修正点用橘色圆圈标出),(b)原始残差与计算出的仅由振动导致的条纹残差Fig.12.(a) The fringe signals before and after vibration correction with the fitted curve as the reference (with the typical corrected data marked by orange circles),and (b) the fitting residual of the fringe signals,calculated from the 1st dataset of measurement.
实际上还可以采用基于黄金分割原理的二维搜索方法重新编写振动补偿算法流程,以实现对最优延时系数τopt和最优增益系数Kopt的全局搜索.计算结果表明,此时振动补偿算法的效果与表3 所示的分别搜索τopt和Kopt时的效果相当.这也再次证明(9)式所示的传递函数简化模型具有合理性.
基于表3 所列的10 组干涉条纹及后续测量得到的50 组干涉条纹进行计算的结果如图13 所示,其中图13(a)为这60 组条纹各自修正前的残差标准差σm以及修正后的残差标准差σc,图13(b)为由此得到的σc相对于σm的衰减比.可以看出每组条纹残差标准差的衰减比的均值仍为45%左右,且分布特征具有随机性,导致该随机性分布最可能的原因仍是原始数据中其他相位噪声造成的随机干扰.

图13 修正前后60 组实测干涉条纹的(a)残差标准差和(b)残差标准差的衰减比Fig.13.(a) The standard deviations of the fitting residuals of 60 sets of fringe signals with and without the vibration correction,and (b) the reducing factor between them.
如前所述,进行本实验时NIM-AGRb-1 型重力仪工作在条纹扫描模式,重力仪本身不输出依据干涉条纹得到的重力测值g.此时,为了分析该振动补偿算法对重力测值的影响,可以参考浙江大学提出的方法[19]计算重力测值的离散度:1)对每一组条纹进行余弦拟合时,进一步计算拟合曲线的初相位φinitial(n)(n为条纹序号,n=1,2,···);2)去除φinitial(n)的均值,得到初相位的偏差序列Δφinitial(n);3)根据(4)式,可得重力偏差序列

也就是说,基于修正前后的干涉条纹P(ΔФth)和P(ΔФvib),可以依据(12)式得到振动补偿前后的重力偏差序列Δgm(n)和Δgc(n).由于本实验所在的测量环境无固定振源,仅有与测量过程在时间上不相关的地脉动、轻微的人员走动或实验楼外的车辆移动等随机振源,理论上参考镜振动只影响重力测值的离散度,不会产生恒定的系统误差.因此补偿前后重力偏差序列Δgm(n)和Δgc(n)的对比可以合理地说明该振动补偿算法的有效性.
根据上述分析,由修正前后的条纹数据得到的修正前后的重力偏差如图14 所示.对全部60 组数据,振动补偿后重力测值的离散度相比补偿前降低了一半左右;由修正前的实测条纹P(ΔФth)得到的重力偏差Δgm的标准差为σgm=51.5 µGal,而由修正后的条纹P(ΔФvib)得到的重力偏差Δgc的标准差σgc=22.0 µGal.σgc相对于σgm的衰减幅度达到57.3%,说明通过该振动补偿算法提高干涉条纹的拟合精度可以显著提升重力测量的精度.
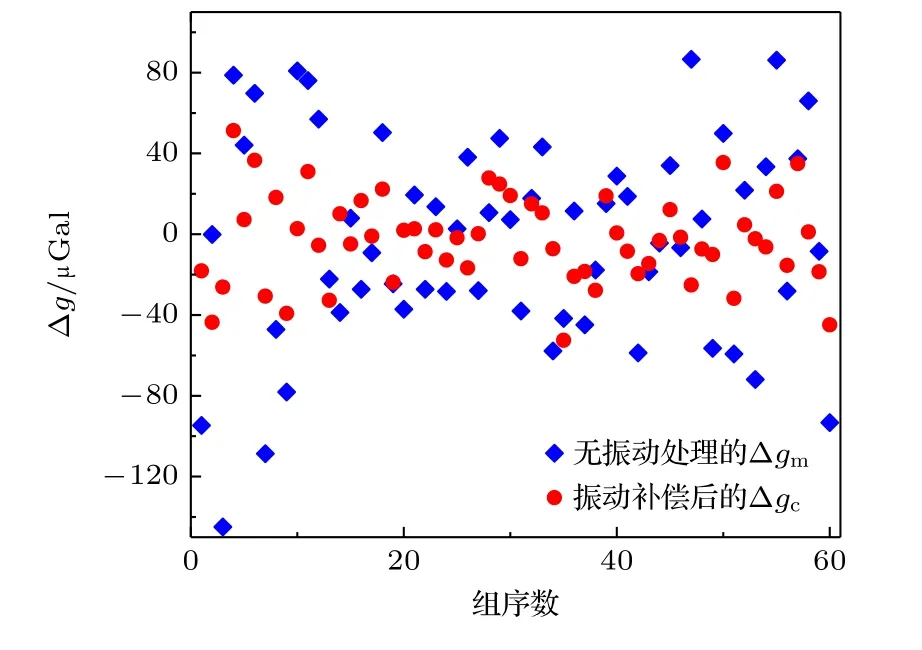
图14 由60 组实测干涉条纹得到的修正前后的重力偏差Fig.14.The variation of the measured g value deduced from 60 sets of fringe signals with and without the vibration correction.
目前NIM-AGRb-1 型原子重力仪作为计量基准装置已被设定为长期工作在第二种重力测量模式,即扫频速率α处于锁定状态,无法直接采用本文提出的振动补偿算法进行测量.因此本文仍以考察该算法对原子干涉条纹残差的衰减效果为主.目前实验室正在研制采用条纹扫描模式来长期工作的可移动式原子重力仪,该振动补偿算法也将配合此重力仪在不同的测试环境中进行长期测量,验证其对包括阿伦方差、重力测量灵敏度在内的关键重力参数的提升效果.
5 讨论
在前述仿真和实验过程中,振动补偿算法查找最优延时系数时的优化目标是拟合条纹时的RMSE 值,即取RMSE 达到其最小值时对应的延时系数为最优延时系数τopt.另一方面,根据理论分析及图6(b)、图8(b)和图11(b)所示的仿真、实测结果,理论上振动补偿效果好时,从地震计信号推算出的仅受振动影响时的条纹相对于理论条纹的残差Rv(ΔФth)非常接近原始条纹相对于理论条纹的残差Rm(ΔФth).因此,参考基于相同简化模型的振动补偿方法在光学重力仪中的算法流程[27],实际上还可以尝试以Rv和Rm的相关系数CR作为优化目标搜索最优延时系数τopt.
相关系数表示2 个列向量之间线性相关的程度,取值范围为—1 至1,绝对值越大表示相关性越强[33].因此,相关系数CR的绝对值越大,说明Rv(ΔФth)和Rm(ΔФth)越接近,即推算出的振动相位Δφvib越准确,则修正后的条纹越接近拟合曲线,其RMSE值应趋于最小值.需要说明的是,计算相关系数CR时需要对Rc和Rv进行归一化处理,因此无法以其为优化目标来搜索最优增益系数Kopt.
以CR达到最大值时对应的延时系数为最优延时系数τopt,相应的仿真和实测数据的计算结果分别如表4 和表5 所示.总体而言,采用两种优化目标时分别计算出的最优延时系数τopt非常接近.如图15 所示,RMSE 值随延时系数的变化曲线与相关系数CR随延时系数的变化曲线具有几乎完全相同的变化规律,但变化方向相反,符合理论预期.个别情况下采用两种优化目标时分别计算出的最优延时系数τopt存在毫秒量级的差异,例如表4中第4 种情况和表4 中第2 组数据,其中前者对延时系数的遍历搜索结果如图15(d)所示,RMSE 值达到最小值时的延时系数和相关系数CR达到最大值时的延时系数略有区别(分别用黑色和粉色点划线标出).导致这种情况最可能的原因仍是原始数据中其他相位噪声造成的随机干扰.

表4 以相关系数CR 为优化目标时的仿真运算结果Table 4.Simulated results with the correlation value CR as the objective of the algorithm.
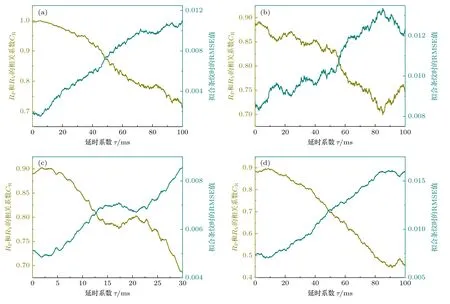
图15 拟合RMSE 值和相关系数CR 与延时系数的关系 (a) 仿真时的第1 种情况;(b) 仿真时的第2 种情况;(c) 实测时的第1 组数据;(d) 仿真时的第4 种情况Fig.15.The RMSE value of fringe fitting and the correlation value CR between the fitting residual of fringes before and after the vibration correction as a function of time delay of (a) 1st simulated dataset,(b) 2nd simulated dataset,(c) 1st measured dataset and(d) 4th simulated dataset.
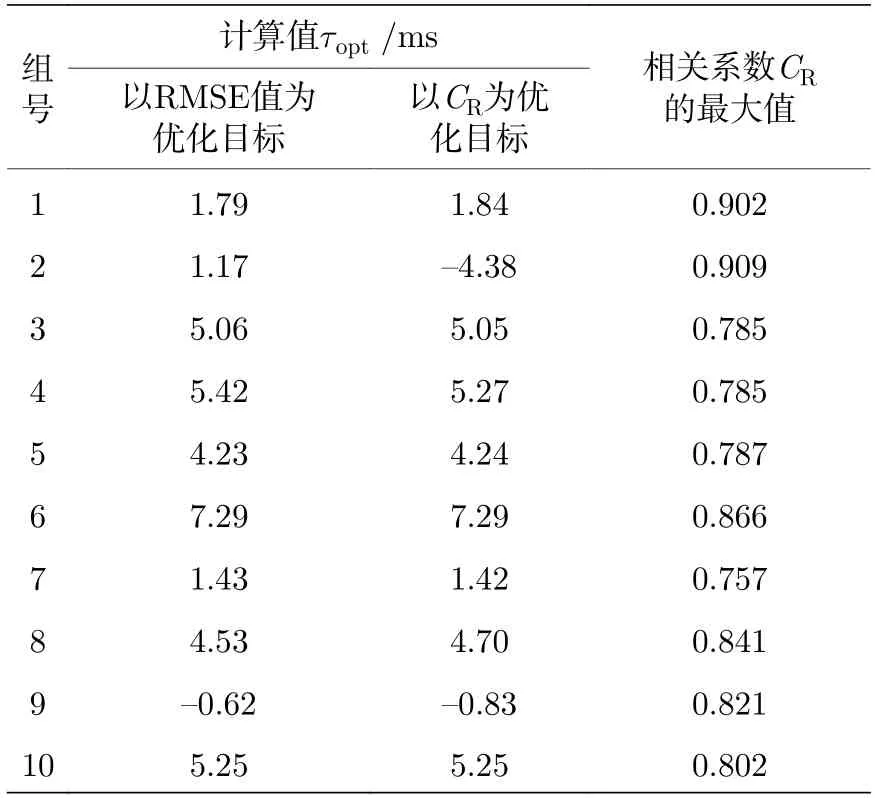
表5 以相关系数CR 为优化目标时的10 组数据的实际测量结果Table 5.Measurement results obtained from 10 data sets with the correlation value CR as the objective of the algorithm.
对每一组数据,依据振动补偿算法计算出最优延时系数τopt和增益系数Kopt后,可以得到最终确定的仅受振动影响时的条纹相对于理论条纹的残差Rv,进而得到最终确定的相关系数CR.图16展示了60 组数据中每一组数据的相关系数CR以及修正后的条纹残差标准差σc相对于修正前的条纹残差标准差σm的衰减比的对应情况.可以看出,相关系数CR越大,σc相对于σm的衰减比也越大,即振动补偿的效果越好.二者的变化趋势完全吻合,与理论预期相符,再次验证了该振动补偿算法原理的合理性.
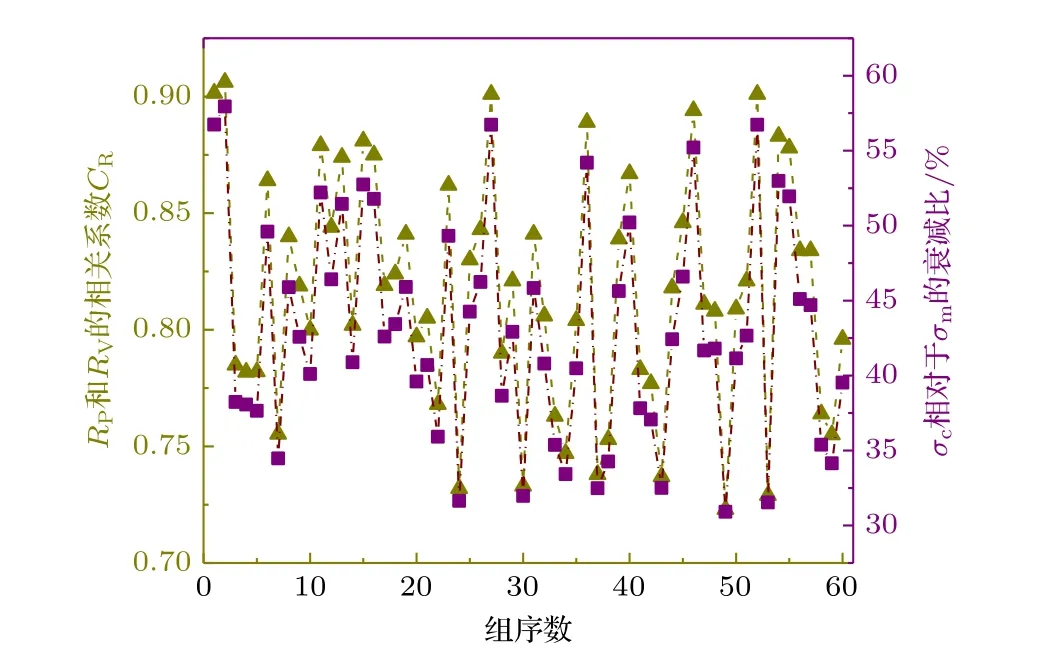
图16 最终确定的Rv 和Rm 的相关系数CR 与修正前后条纹残差标准差的衰减比Fig.16.The correlation value CR between the fitting residual of fringes before and after the vibration correction,and the corresponding reducing factor of the standard deviation of the fitting residuals of fringe signals after the vibration correction.
还可以直接以2.3 节提出的条纹残差标准差这一指标作为振动补偿的优化目标,即取(11)式所示的标准差σc达到最小值时的延时系数和增益系数为最优值.相应的仿真及实测数据的计算结果表明,在绝大多数情况下以RMSE 值或σc为优化目标时搜索出的τopt和Kopt均完全相同.个别情况下搜索出的延时系数存在毫秒量级的差异,增益系数也可能存在微小差异,如表6 所示.导致这种结果最可能的原因仍是原始数据中其他相位噪声造成的随机干扰.

表6 以残差标准差为优化目标时的仿真及实测数据运算结果Table 6.Simulated and measurement results with the standard deviation of the fitting residuals as the objective of the algorithm.
综上,当原子重力仪在振动条件更复杂的环境中测量时,即振动相位Δφvib的影响远大于其他相位噪声Δφothers的影响时,该振动补偿算法的计算
精度和对条纹的修正效果有望得到进一步提升.在后续工作中,该振动补偿算法将配合实验室正在研制的可移动式原子重力仪在复杂环境中进行测试.
总体而言,本文在第2 节定性分析了原子重力仪所用参考镜与振动传感器之间的传递函数简化模型中的延时系数τ和增益系数K发生变化的原因,描述了对这两项系数进行搜索求解的具体振动补偿算法流程;在第3 节采用不同的仿真输入对算法的有效性进行了详细的定量论证;在第4 节利用重力仪在非常安静的环境中的实测数据验证了该算法对原子干涉条纹以及重力测值的补偿效果.该算法最大的优点是自适应性较强:相比现有的其他振动补偿研究成果,它具有较强的技术意义,可以直接应用于任何能够扫描出干涉条纹的原子重力仪在任意时间和地点的测量结果,以实现对传递函数中的两项关键系数的实时标定,实现当前最好的振动补偿效果.另一方面,受限于NIM-AGRb-1型原子重力仪的体积、工作模式和测试任务,该算法的有效性还未能在较为复杂的振动环境中进行验证;而目前也尚无现有的其他振动补偿方法在与本次实验相同的安静环境中应用于与该重力仪精度水平相当的原子重力仪上的实验数据.从该算法与其他振动补偿方法在不同测量环境及具有不同噪声水平的原子重力仪上的实验结果来看,该算法尚未展现出显著优于其他方法的补偿效果,有待更进一步的测试验证,其工作原理和具体流程也将在后续工作中不断优化.
6 结论
应用于原子干涉式绝对重力仪的振动补偿方法的主要作用是修正参考镜振动引入的相位噪声,从而提高干涉条纹的拟合精度,最终提高重力加速度g的测量精度.现有的振动补偿方法在确定的静态或动态环境中可以实现较高的测量精度,但大部分公开成果没有介绍对于因测量环境改变而产生的原子重力仪中某些部件的机械传递函数的变化进行实时修正的具体应对流程.从长期稳定性的角度来看,这可能在一定程度上限制重力仪在不同环境尤其是复杂振动环境的测量精度.本文介绍了一种应用于原子重力仪的基于搜索传递函数简化模型系数的振动补偿方法,着重描述了其具体的算法流程,并利用仿真及实测结果对其合理性和有效性进行了详细论证.具体而言,该方法将参考镜的振动信号与测量该振动的传感器的实际输出信号之间的真实传递函数简化为一个延时系数和一个增益系数的结合,通过计算软件对重力仪的干涉条纹和传感器的输出信号进行分析,搜索出当前测量环境下这两个系数的最优估算值,由此可以更加精确地推算出当前环境下参考镜的真实振动信号.该方法具有自适应性,可以在测量环境改变时对结构的真实传递函数进行合理估算,以实现在当时当地对原子干涉条纹最好的修正效果.实测结果表明,在极为安静的环境中,本文提出的振动补偿算法可以将原子重力仪干涉条纹的余弦拟合残差的标准差大幅衰减,最大衰减幅度达到58%.利用修正后的干涉条纹计算出的重力值的标准差相比修正前衰减57%.根据理论分析和仿真运算,在复杂振动环境中进行重力测量时,该算法将表现出更好的干涉条纹修正效果.因此,该振动补偿算法有望直接应用在不同时刻和不同地点对原子重力仪测量结果的实时修正,提高原子重力仪在不同环境尤其是复杂振动环境中的测量精度,其补偿效果也将在之后的工作中进行更充分的验证及优化.

