环面黑洞的热力学函数

管韵 王波波

1) (北京交通大学理学院,北京 100044)

2) (山东大学(威海)空间科学与物理学院,威海 264209)

1 引言

自Bekenstein[1,2]发现黑洞动力学系统与热力学系统的相似性、霍金证明黑洞存在热辐射[3]以来,黑洞热力学一直是理论研究的热点之一.人们研究了史瓦西黑洞、Reissner-Nordstrom (RN)黑洞以及Kerr-Newman 黑洞的热辐射谱、温度以及黑洞熵.

求解带有宇宙学常数λ的爱因斯坦场方程,可以得到λ＞ 0 的de Sitter 黑洞(如Schwarzschildde Sitter黑洞,Reissner-Nordstrom-de Sitter 黑洞,Kerr-Newman-de Sitter 黑洞等)和相应的λ＜ 0的Anti-de Sitter(AdS)黑洞.人们发现这些黑洞具有不为零的温度和熵,是真实的热力学系统.最初宇宙常数λ是被当作一个常数(参数)引入的,它不是一个动力学变量.但是,越来越多的研究表明,在黑洞热力学中应该把λ看成是动力学变量[4-10].主要原因为[11]:1) 人们可以考虑“更基本”的理论,其中物理常数如规范耦合常数、牛顿引力常数或宇宙常数不是先验固定的,而是作为真空期望值出现,因此宇宙学常数λ应该可以变化;2) 在宇宙常数存在的情况下,黑洞热力学第一定律变得与Smarr 关系不一致(标度论证不再有效),除非在第一定律中包含宇宙常数λ的变化;3) 一旦将λ的变化包含在第一定律中,黑洞质量就被确定为焓而不是内能.也就是在一个扩展的相空间中应该把宇宙学常数λ当成热力学压强其中AdS 半径(这里λ＜0,仅考虑AdS黑洞),与压强共轭的变量就是黑洞的体积V.引入压强和体积这两个动力学(热力学)变量后,其相空间增加了两个新的维度,通常称其为扩展相空间.例如,带电的AdS 黑洞的热力学第一定律在扩展相空间中的形式为[12]

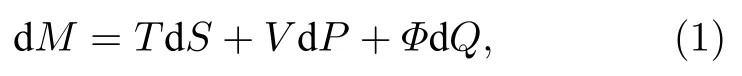
其中,M为黑洞质量,T为黑洞温度,Φ是黑洞表面的电势,Q是黑洞电荷量,为黑洞的体积,这里r+是该黑洞事件视界的半径.文献[12]在扩展的相空间中研究了带电AdS 黑洞的热力学性质,求出了其热力学状态方程,通过计算欧氏作用量得到了吉布斯自由能G,并由此求得熵S、热容等热力学量.

通常人们研究比较多的黑洞,比如史瓦西黑洞、RN 黑洞以及Kerr-Newman 黑洞等,它们的时间坐标t为常数和径向坐标r为常数的曲面的拓扑为S2.而环面黑洞相应的曲面拓扑为S1×S1(见第2 节的简介).人们研究发现,与通常的黑洞一样,环面黑洞也是一个热力学系统,具有温度和熵[13,14].据我们所知,还没有人将宇宙学常数当成动力学变量来研究环面黑洞.也还没有人求出环面黑洞熵和温度之外的热力学函数.本文研究的问题是:1) 环面黑洞是不是与带电的AdS 黑洞一样,具有范德瓦耳斯型的相变;2) 求出环面黑洞的热力学状态方程、以及其他热力学函数.

本文利用扩展相空间,求得环面黑洞的状态方程、欧氏作用量以及吉布斯自由能.再利用基本热力学函数公式,求得环面黑洞的自由能、内能、焓以及定压热容和定容热容.第2 节将简单介绍环面黑洞的基本性质;第3 节求环面黑洞的状态方程,以及热力学第一定律;第4 节推导环面黑洞的Smarr 关系;第5 节计算环面黑洞的欧氏作用量;第6 节计算吉布斯自由能等热力学函数,以及定压和定容热容;最后第7 节是总结和讨论.

2 环面黑洞的基本性质

带宇宙常数λ的爱因斯坦场方程有一个平面对称解[15,16],

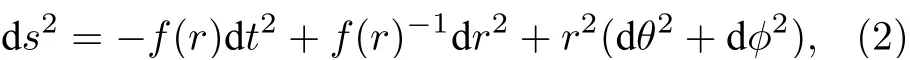
其中

可以通过认同的方式将(2)式转化为环面黑洞解[16].分别认同以及①文献[16]是认同 θ=0 和 θ=2π 以及ϕ=0和 ϕ=2π,与本文采用的认同方式没有本质区别.,得到一个环面时空解[13],其t=常数和r=常数的曲面是一个环面,拓扑为S1×S1.利用高斯定理可得b=Q;计算ADM 质量M,得M=a/2 .可以把(2)式和(3)式重新表示为

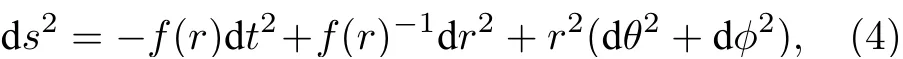
其中A为规范势,

3 环面黑洞的状态方程与黑洞热力学第一定律

与球对称黑洞相同,环面黑洞的温度T也正比于黑洞视界的表面引力κ,即黑洞温度为

表面重力的计算公式为[17]

于是环面黑洞的温度为

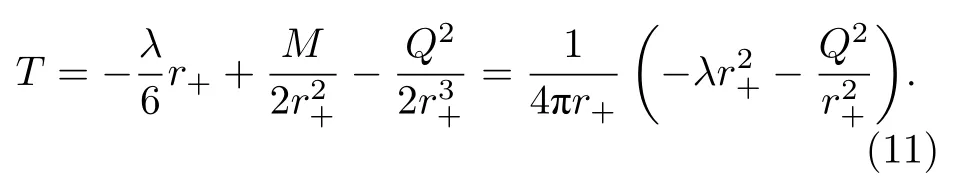
计算(11)式应用了f(r+)=0,即

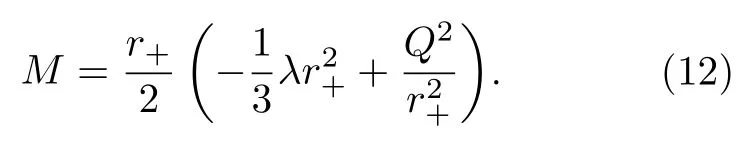
第1 节提到,人们认定AdS 黑洞的热力学压强P与宇宙常数λ的关系是

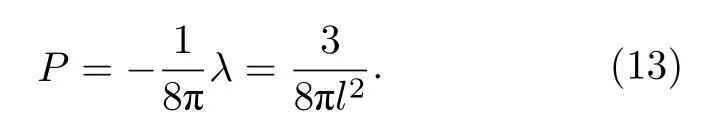
类似地,在研究环面黑洞热力学性质时,也应该考虑λ的变化,并且压强与宇宙常数的关系依然如(13)式所示.与压强共轭的热力学量是环面黑洞的体积,即

可将(11)式改写为

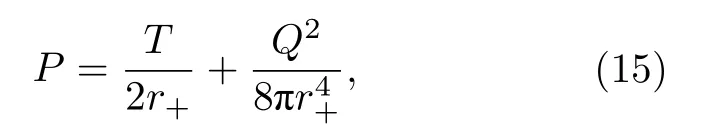
其中r+=V是黑洞的热力学体积,T是黑洞的温度,Q是总电量.这里将黑洞的总电量Q视为常数,而非热力学变量.

在球对称AdS 黑洞中,研究黑洞相变时常采用比体积v=2r+,而不是体积V来表示状态方程.改用比体积v,则(15)式可改写为

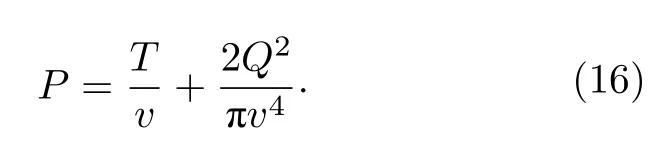
将比体积v视为自变量,在等温条件下,压强P单调递减,故不存在相变临界点,环面黑洞不具有范德瓦耳斯型的相变.环面黑洞的等温曲线如图1所示.可以看到,当比体积v增加时,压强P单调下降.从上到下3 条曲线对应的温度分别是T=50,25,1,其中电荷Q=1 .

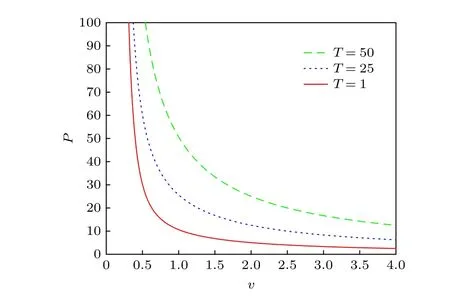
图1 环面黑洞的等温图Fig.1.Isotherm of toroidal black hole.

将黑洞质量M看成是黑洞视界面积A、压强P和电量Q的函数,(12)式可以改写为

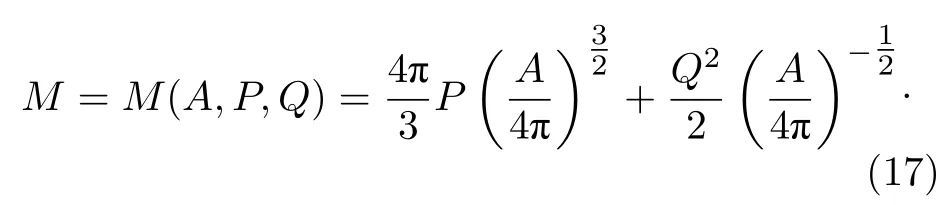
质量M的全微分可以表示为

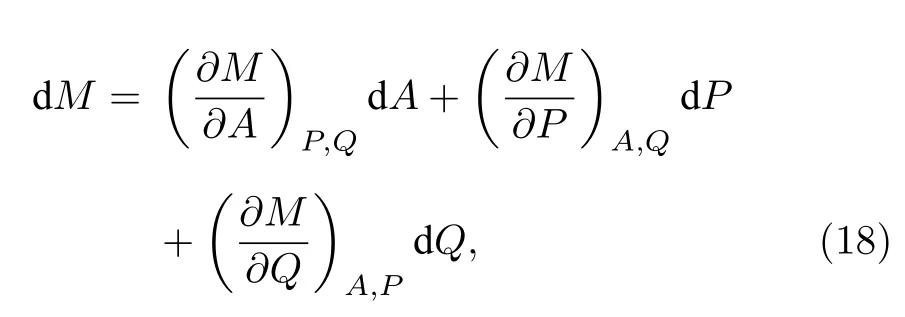
即

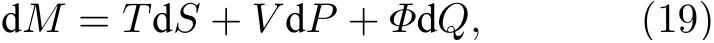
其中

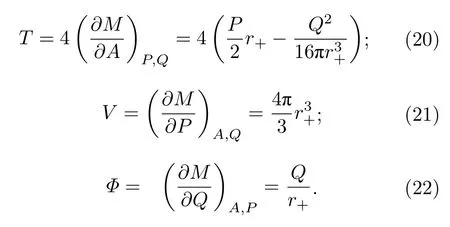
(19)式就是环面黑洞的热力学第一定律.

4 环面黑洞的Smarr 关系

利用齐次函数的欧拉定理,可以方便地得到环面黑洞的Smarr 关系.加权齐次函数的欧拉定理(Euler’s theorem on weighted homogeneous functions),即若多元函数f(x,y,z) 满足标度关系(scaling relation):

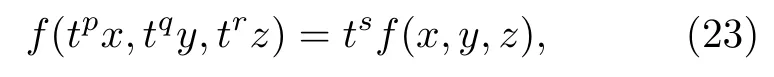
则该函数及其偏微分满足

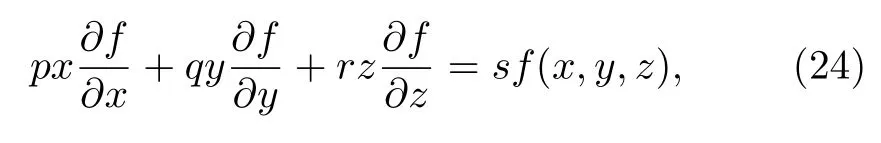
(24)式的证明参见附录A.

为了利用欧拉公式确定Smarr 关系,需要用到标度论证方法[5,18,19].环面黑洞的度规表达式(5)式采用的是自然单位制,把长度的量纲记为L,可以看出:宇宙学常数λ的量纲是L-2,质量M和电量Q的量纲均是L.另外,黑洞事件视界面积A=的量纲是L2.也就是对于一个长度标度l,有

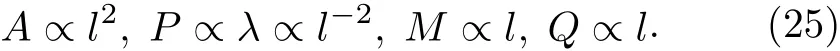
把质量M看成是事件视界面积A、压强P以及电量Q的函数,M=M(A,P,Q),利用上述欧拉定理,得

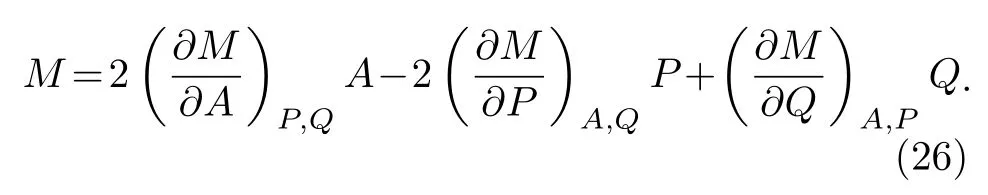
将(20)式—(22)式中的3 个偏导数代入,得到环面黑洞的Smarr 关系

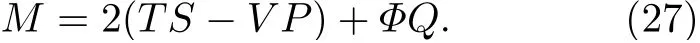
5 环面黑洞的欧氏作用量

欧氏作用量能给出不同系综的热力学势,而不同的系综与边界条件的选取有关[11].计算欧氏作用量通常会得到一个发散的结果,为了消除这个发散,可以减去一个适当的背景时空的欧氏作用量.有不同的选取背景时空的方法,不同的选择会导致不同的结果.我们采用Caldarelli 等[4]的方法计算欧氏作用量.

对环面时空线元(4)式的时间坐标做变换t →iτ,得其欧氏度规的线元,

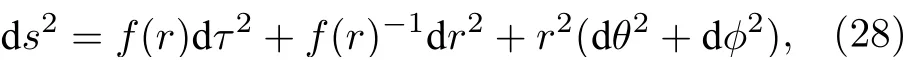
其中函数f(r) 依然为(5)式表示.

欧氏作用量由三部分组成:

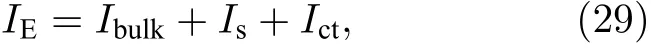
其中,Ibulk为bulk 作用量;Is为作用量的表面项,是在一个超曲面上积分;Ict称为欧氏作用量的补偿项,又称背景时空项,是为了消除作用量的发散而引入的.作用量的bulk 项为[4]

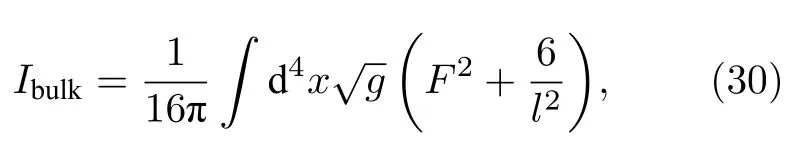
(30)式采用了G=1 的单位制,其中二形式(2-form)的电磁张量为

这里

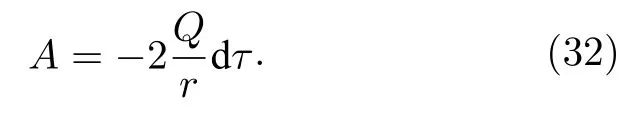
由此可得电磁张量的非零分量为

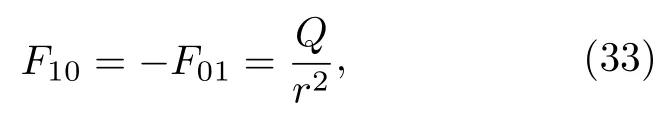
直接计算得

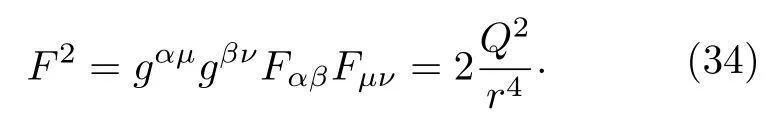
将(34)式代入(30)式,坐标τ的积分从 0→β(β为温度的倒数);坐标r的积分从事件视界表面r+→∞(由于积分发散,暂时记积分上限为r,最后取极限r →∞),而两个角度积分均从具体计算得

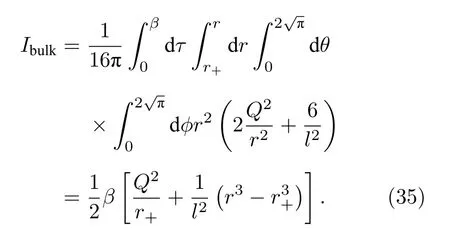
作用量的表面项为[4]

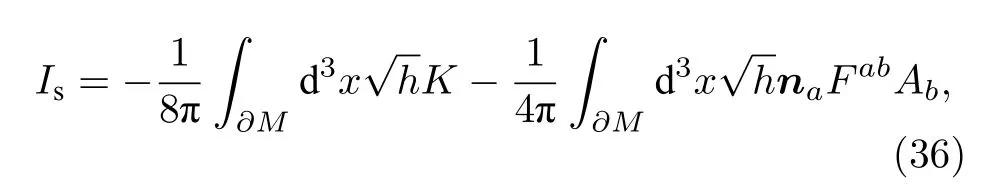
其中标量外曲率

这里Kab是r=常数的超曲面的外曲率.hab为该超曲面的度规,可具体表示为

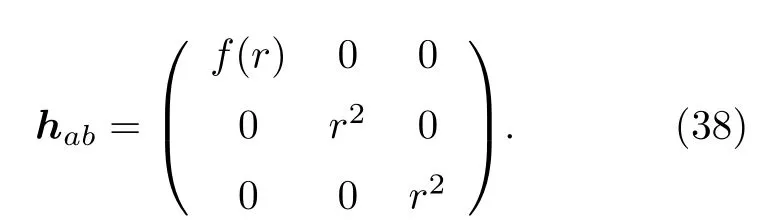
由此得

超曲面度规的逆变分量为

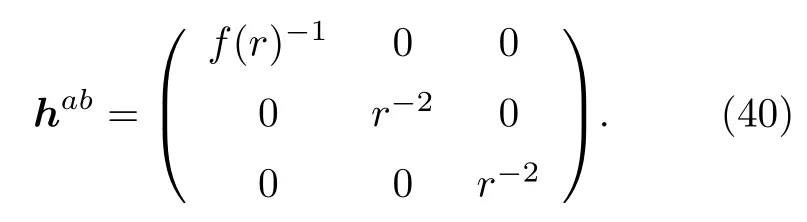
外曲率定义为

其中超曲面的法余矢

这里

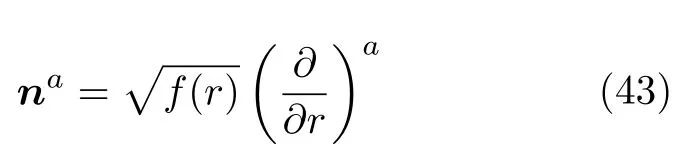
是该超曲面的法矢量.直接计算得到:

另外,由(32)式、(33)式,以及(43)式可得

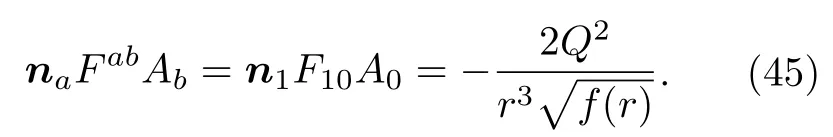
将(44)式和(45)式代入(36)式,得

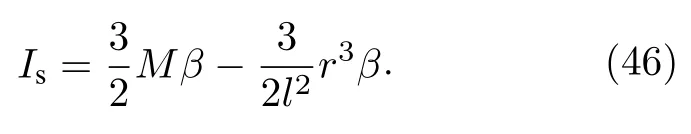
当r →∞时,分别从(35)式和(46)式可以看到,Ibulk和Is均发散.采用Caldarelli 等[4]的方案来消除发散,即采用下面的补偿项:

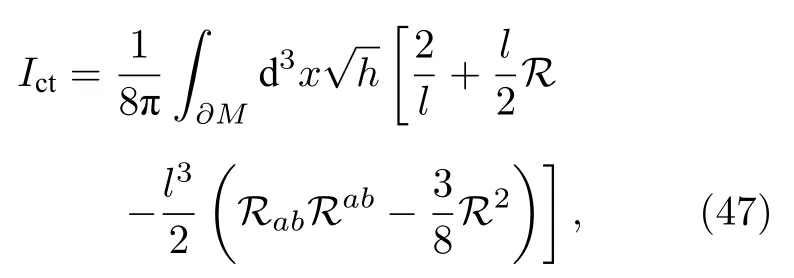
其中Rab为该超曲面的里奇张量,R=habRab为里奇标量曲率.对于(28)式的度规,R=0,Rab=0 .计算(47)式,得

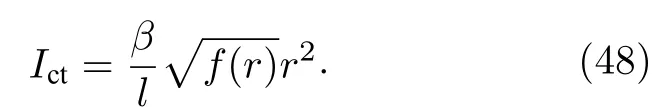
注意到当r →∞时,

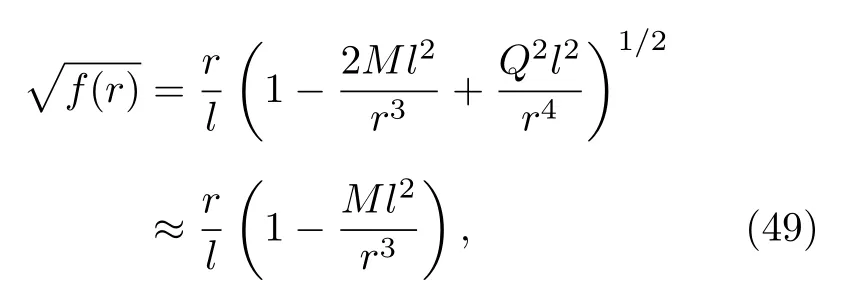
所以

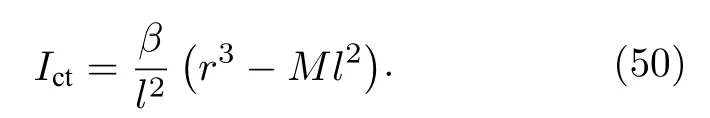
最后,将作用量的bulk 项(35)式、表面项(46)式以及补偿项(50)式代入(29)式,得环面黑洞的欧氏作用量

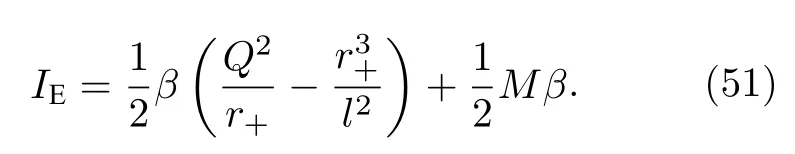
将质量表示式(12)式代入(51)式,得

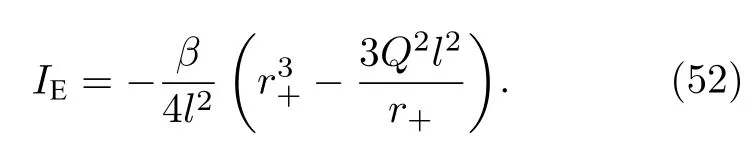
6 环面黑洞的热力学函数

第5 节计算欧氏作用量所取的边界条件相当于采用了正则系综,故系统的吉布斯自由能[4]为G=IE/β.将(52)式代入(51)式,得环面黑洞的吉布斯自由能为

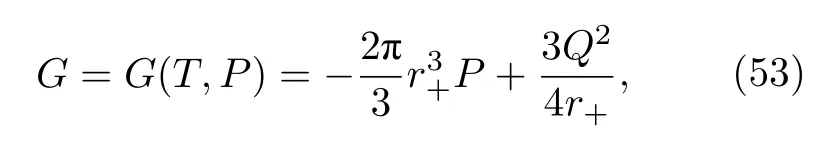
这里,r+应该理解为压强和温度的函数,即r+=r+(P,T),正如(15)式所示.吉布斯自由能与温度T、压强P的关系如图2 所示,图中没有范德瓦耳斯型的燕尾形状(swallowtail behaviour),这也说明环面黑洞没有范德瓦耳斯形式的相变.

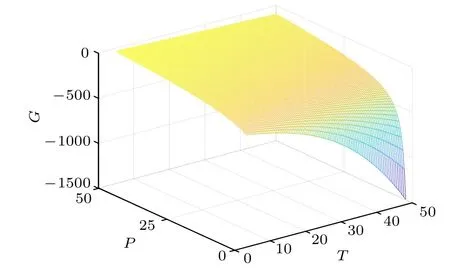
图2 环面黑洞吉布斯函数Fig.2.Gibbs function of toroidal black hole.

吉布斯自由能的微分可表示为

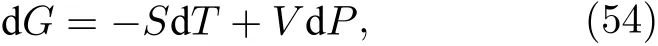
其中,熵为

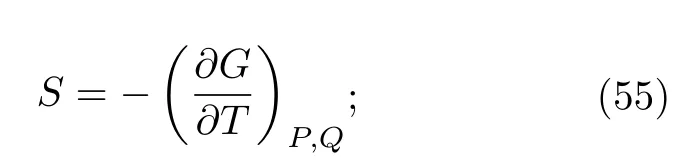
体积为

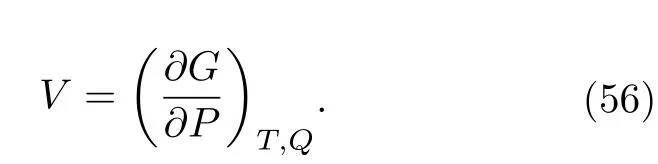
将吉布斯函数(53)式代入(55)式,并利用状态方程(15)式,可以得到

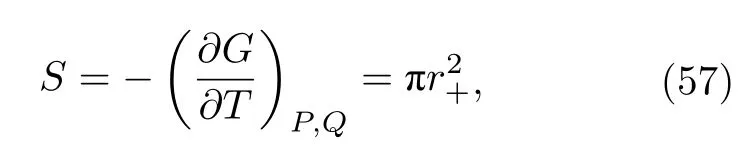
这个结果与其他方法得到的熵的表示式相同.

环面黑洞的定压热容为

由此可见,环面黑洞是一个稳定的热力学系统.

有了吉布斯函数,其他热力学函数也可以容易地求得.例如,自由能

由此可见,内能是r+(或体积V)的单值函数.环面黑洞的焓为

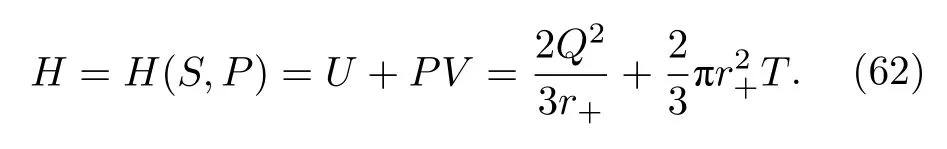
7 结论

本文将宇宙学常数视作变量,在扩展的相空间中研究了环面黑洞的热力学性质.这个扩展的相空间是在原有的相空间上增加了压强P和体积V这一对热力学共轭量.压强体积这里r+是环面黑洞的事件视界半径.本文求得环面黑洞的状态方程、Smarr 关系,以及环面黑洞的欧氏作用量、吉布斯自由能(吉布斯函数)G、自由能F、内能U和焓H、定压热容和定容热容.我们注意到环面黑洞的Smarr 关系(27)式与带电AdS 黑洞的Smarr 关系相同[12].

从状态方程(16)式以及吉布斯函数(53)式可以看出,环面黑洞没有范德瓦耳斯型的相变.如图1的等温线所示,压强P随比体积v单调下降,没有范德瓦耳斯等温线那样的一个极小值和一个极大值,所以不会有范德瓦耳斯型的相变发生.另外,图2 绘制的吉布斯函数曲面,也没有范德瓦耳斯相变的燕尾形状,也说明没有范德瓦耳斯型形变.

有必要把环面黑洞与带电AdS 黑洞做个比较.它们的热力学第一定律以及Smarr 关系相同,但其状态方程不一样.另外,二者除了熵函数的形式(S=)相同外,其他热力学函数形式都不一样.这说明时空拓扑结构影响黑洞的热力学性质.

附录A 加权齐次函数欧拉定理的证明

若f(x,y,z) 满足

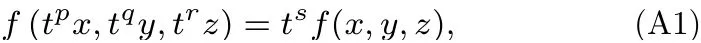
则称f(x,y,z) 为加权齐次函数.令x′=tpx,y′=tqy,z′=trz.(A1)式两边对t求导数,得

(A2)式中令t=1,则得到

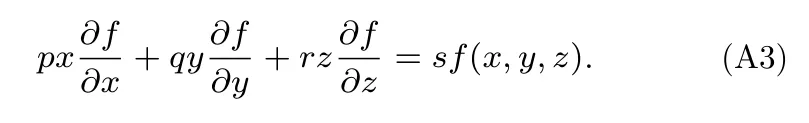
这正是加权齐次函数欧拉定理.证毕.