NbOx 忆阻神经元的设计及其在尖峰神经网络中的应用*

古亚娜 梁燕† 王光义 夏晨阳

1) (杭州电子科技大学电子信息学院,杭州 310018)

2) (中国矿业大学电气工程学院,江苏省煤矿电气与自动化工程实验室,徐州 221116)

1 引言

自1971 年提出忆阻器的概念[1],到2008 年惠普实验室报道了忆阻器[2]的物理实现,围绕忆阻器的相关研究层出不穷.针对高效能计算面临的存储墙和功耗墙问题,忆阻器由于其低功耗、纳米级、可扩展性和非易失性等特点[3-6],成为制造人工神经元和突触的理想候选者,在神经形态计算领域具有巨大的应用前景.

忆阻器分为无源忆阻器和局部有源忆阻器,无源忆阻器由于其电导可控性和非易失性,可以用来模拟生物突触[7].局部有源忆阻器利用其负微分电阻(negative differential resistance,NDR)特性,可实现对无限小信号的放大,进而具有将直流信号转换为交流信号的能力,可用于构建人工神经元[8].

2014 年蔡少棠教授提出局部有源是复杂性的起源,复杂和丰富的动力学行为仅出现在局部有源系统[9-12].局部有源忆阻器(locally-active memristor,LAM),不同于无源忆阻器,其直流电压-电流(V-I)特性中一定存在NDR,即负斜率区域.研究表明,NbOx,TaOx,TiOx和VO2是一类可展现局部有源特性的忆阻材料[13].

目前,局部有源忆阻器的理论分析主要针对通用型LAM 的理论模型,对扩展型LAM 器件的物理模型研究较少.文献[14]根据蔡氏展开定理提出了一种通用型LAM 的理论模型,并构建了周期和混沌振荡电路,采用小信号分析、Hopf 分岔分析等方法研究了LAM 小信号等效电路和振荡电路.文献[15]针对蔡氏结型忆阻器展开了理论分析,并采用小信号分析等方法确定了二阶振荡电路的结构及参数取值范围,为压控型LAM 振荡电路的设计奠定了理论基础.

已有相关研究成果表明,LAM 可用于构建人工神经元,其具有全或无、动作电位、尖峰周期振荡等神经行为.文献[16]采用蔡氏结型忆阻器小信号等效电路参数精确定位其混沌边缘的条件,并设计了基于蔡氏结型忆阻器的神经元电路,验证了其具有的典型神经形态行为.文献[17]主要采用两个纳米级VO2LAM 和两个电容构建了HH (Hodgkin-Huxley)神经元模型,实验结果表明其具有23 种神经形态行为.文献[18]中提出了一个非易失的LAM 数学模型,并将其应用在HR (Hindmarsh-Rose)神经元中,可产生四种共存的神经脉冲行为.文献[19]基于NbOxLAM 设计了一种LIF(leaky integrate-and-fire)神经元,并将SFA (spike frequency adaptation) 行为整合到神经元中,建立了相应的自适应神经元模型.

神经形态计算因其低能耗而受到了广泛的关注[20],受大脑启发的神经形态硬件也已经显示出了在节能计算方面的巨大潜力.2017 年,文献[21]提出了一种称为记忆训练的忆阻器架构,用于在RRAM内存中实现神经网络的训练.文献[22]建立了一个全忆阻尖峰神经网络(256×5),并通过实验验证了其奥利维蒂的面部模式识别功能.

在众多LAM 纳米器件中,NbOxMott 忆阻器件在神经形态计算中应用较多[23,24].它的开关行为可以通过与热反馈效应相关的弗伦克尔-普尔传导机制解释,但其物理模型的复杂性使得对其电路理论分析更加困难,同时也使得NbOx忆阻器在周期振荡器、尖峰神经元方面的应用缺乏电路理论依据,故对其物理模型的理论分析是至关重要的.

本文针对NbOx忆阻器的物理模型展开了深入的理论研究,在第2 节中分析了NbOx忆阻器的直流V-I特性、小信号分析、频率响应以及Hopf分岔点.第3 节中建立了一个基于NbOx忆阻器的二阶电路,分析了二阶电路的雅可比矩阵特征根的位点变化情况和二阶电路振荡的条件.第4 节在二阶电路的基础上添加了一个运算放大器构成尖峰神经元,并设计了尖峰神经网络,用于模式识别.

2 NbOx 忆阻器物理模型及其特性分析

NbOxLAM 具有电流控制的S 型NDR 特性,其开关行为可以通过与热反馈效应相关的弗伦克尔-普尔式传导机制来解释,其电压-电流关系被描述为[25]

其中vm表示忆阻器两端的电压;im表示通过忆阻器的电流;T是忆阻器内部的温度(状态变量);R0,α0,α1和α2是模型的参数;Cth和Γth分别表示热电容和电导;Tamb代表环境温度.模型参数的取值为

2.1 捏滞曲线

蔡少棠教授在2011 年撰文提出,不管何种阻变材料或何种物理机制,二端器件只要能够展现出捏滞曲线(pinched hysteresis loop,PHL)这一特征,就是忆阻器[26].之后他又于2013 年总结了忆阻器的三个典型特性[27].

当忆阻器的激励为v(t)=2 sin(2πft)正弦电压信号,频率分别为1 MHz,10 MHz 和1 GHz 时,S 型NbOxLAM 的vm-im特性曲线如图1 所示.从图1 中可以观察到,S 型LAM 在一个零均值的正弦信号下,其PHL 分布在vm-im平面上的第一象限和第三象限.此外,图1 还表明了PHL 的频率依赖性:PHL 的闭合面积随着频率的增加而单调减小,最终收缩为一条直线.

图1 S 型NbOx LAM响应 于1 MHz,10 MHz,1 GHz 的正弦信号的捏滞曲线Fig.1.Pinch hysteresis curves of S-type NbOx LAM in response to sinusoidal signals at 1 MHz,10 MHz and 1 GHz.

2.2 直流电压-电流特性

当不同的直流电流I输入NbOx忆阻器时,可以得到忆阻器的一组电压电流数据,其直流V-I曲线如图2(a)所示.图2(a)电流扫描下的直流V-I图具有连续的S 型NDR 行为.NDR 区域显示为蓝色区域,其中电流和电压范围分别为(0.004 A,0.072 A)和(0.1768 V,0.390 V).从NbOx忆阻器的直流V-I图中可知,如果施加直流电流激励I=I0,则有唯一的电压值V0与其对应,静态工作点为Q(V0,I0).但如果是直流电压激励V=V0,R=0,图2(b)所示的图解法表明V=V0与忆阻器S 型NDR 特性有三个交点Qa(V0,Ia),Q0(V0,I0)和Qb(V0,Ib).其中,Qa和Qb是稳定的工作点,Q0是不稳定的工作点[28].当串联电阻R满足一定条件时可使得NDR 区域内的工作点Q0稳定,图2(b)中的红色实线是负载线I=(VD-V)/R.

图2 NbOx LAM 的直流V-I 图 (a) 浅蓝色部分是忆阻器的NDR 区;(b) 红色线是负载线,插图为电压偏置电路Fig.2.DC V-I plot of NbOx LAM:(a) The light blue part is the NDR region of the memristor;(b) the red line is the load line and the inset is the bias circuit with DC voltage supply.

参数I1,I2,V1和V2决定了产生振荡的静态工作点区间.因此,为了使该忆阻器产生振荡行为,施加的直流电流激励范围是I1—I2,直流电压激励需满足I1R+V1＜V＜I2R+V2.此外,串联电阻R应满足其电导值小于工作点处的斜率,即

2.3 小信号分析

为了对NbOx忆阻器的局部有源特性展开定量分析,采用局部线性化方法,即忽略在工作点处泰勒展开式中的高阶非线性项.假设在直流工作点Q(V0,I0)处施加一个小信号电压δV,产生响应δT和δi.因此,忆阻器电压vm、电流im和温度T可表示为

其中V0=v(Q),T0=T(Q),I0=i(Q).因为是在直流工作点处对忆阻器进行分析,所以关于状态变量T的微分方程取值为0,即忆阻器在直流工作点处的状态变量T0满足

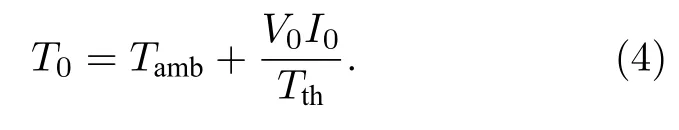
对忆阻器数学模型(1)式在工作点Q处进行泰勒级数展开可得

其中h(T0,V0)是定义NbOx忆阻器的状态微分方程在工作点处的值,由于静态工作点处的状态变量是一定值,即状态微分方程取值为0,故h(T0,V0)=0.然后对(5)式进行拉普拉斯变换,令可以得到s域的泰勒级数展开式:

其中参数a11,a12,b11,b12表示为

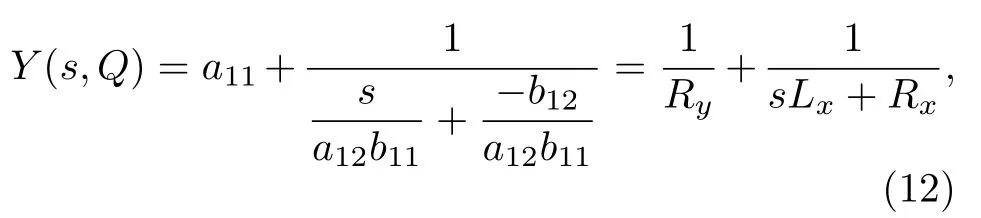
其中Lx=1/(a12b11),Ry=1/a11,Rx=—b12/(a12b11),取值由直流工作点决定.图3 给出了h(V0,T)与温度T的变化关系,曲线与x轴的交点是dT/dt=0 的点,也叫平衡点,P1和P3两点的左边dT/dt＞0,右边dT/dt＜ 0,所以P1点和P3点是稳定的平衡点,同理P2点是不稳定的平衡点.另一方面,P1和P3点的斜率小于0,即b12＜ 0,P2点的斜率大于0,即b12＞ 0.所以可以得出,当工作点处的小信号等效电路中的b12＞ 0 时,该工作点是不稳定的,当工作点处的小信号等效电路中的参数b12＜ 0 时,该工作点是稳定的.

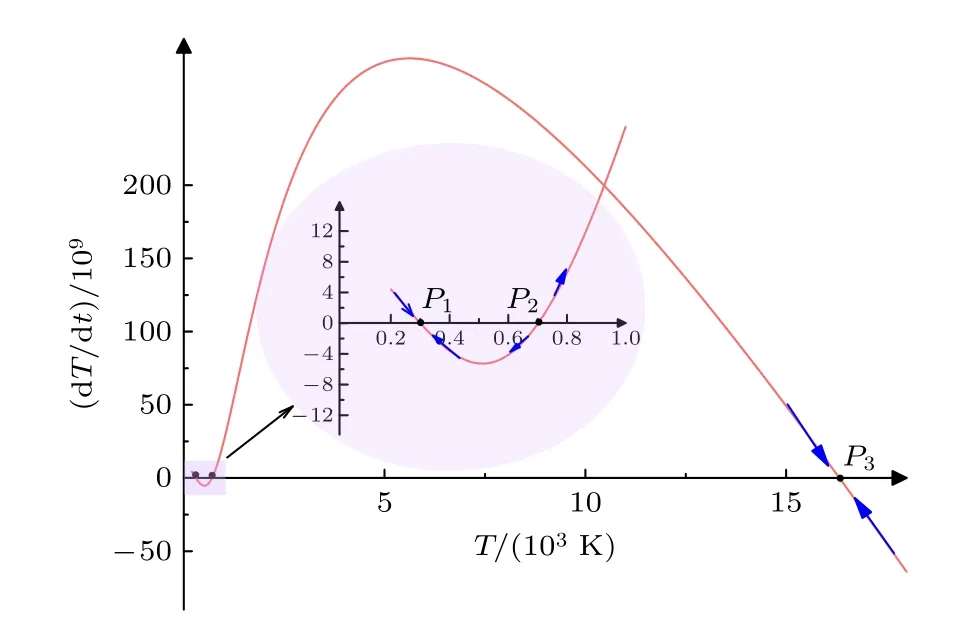
图3 h (V0,T)与温度T 的关系图Fig.3.Relationship between h (V0,T) and temperature T.

将工作点Q(0.008 A,0.3003 V)处的取值代入,可以求得a11=0.0286,a12=4.3873 × 10—5,b11=1.2526 × 1011,b12=5.4481 × 107,可以看出所选取的工作点Q处的参数b12＞ 0,所以Q点是一个不稳定的工作点,需要电流激励来使得工作点稳定.将a11,a12,b11,b12的值代入(12)式,得到小信号等效电路中各个元件的取值分别为Lx=5.346 × 10—8H,Ry=8.266 Ω,Rx=—1.83 Ω,如图4(a)所示.图4(b)—(d)给出了不同工作点对应的小信号等效电路的电路参数取值.蓝色的曲线是电压vm,电流im和等效电路中的三个线性元件之间的依赖关系,棕色的曲线是蓝色曲线在vm-Rx,vm-Lx,vm-Ry平面上的投影,绿色曲线是在im-Rx,im-Lx,im-Ry平面上的投影,红色曲线是在im-vm平面上的投影,除此之外,还给出了在NbOx忆阻器的NDR 区的等效元件结果,从局部放大图中可以看出NDR 区域内,小信号等效元件Rx总为负,小信号等效元件Lx和Ry总为正.其中,负电阻Rx可为忆阻振荡电路提供能量,电感Lx使得忆阻器呈现感性.

图4 (a) NbOx-Mott 忆阻器在工作点Q (0.008 A,0.3003 V)处的小信号等效电路模型;(b) Rx 对工作点的依赖性;(c) Lx 对工作点的依赖性;(d) Ry 对工作点的依赖性Fig.4.(a) Small-signal equivalent circuit model of NbOx-Mott memristor at the operating point Q (0.008 A,0.3003 V);(b) the dependence of Rx on the operating point;(c) the dependence of Lx on the operating point;(d) the dependence of Ry on the operating point.

由于NbOx忆阻器的小信号等效电路包含一个正电感,所以需要并联电容来使电路以一定的频率振荡.为了确定并联电容C的取值范围,需要计算忆阻器导纳的频率响应Y(iω,V0).

令s=iω可以得到忆阻器等效导纳在工作点Q处的频率响应为

其中,实部和虚部分别为

在—1×108rad/s ＜ω＜ 1×108rad/s 范围内,NbOxLAM 在I=0.008 A 处的实部和虚部的变化情况如图5(a)所示.从图5(a)可以观察到,导纳函数的虚部随频率的增大先增大再减小再增大,在ω＞ 0的范围内始终为负.奈奎斯特如图5(b)所示,当实部为0 时,|ω*|=8.68×107,该频率为忆阻器在I=0.008 A 处的临界振荡频率,在正的ω*处ImY(iω,V0)大于0,说明忆阻器在振荡频率ω*=8.68×107处是感性的,因此,需要并联电容补偿导纳的虚部,使复合电路的总导纳虚部为零,可得并联电容的临界值C*满足ω*C*+ImY(iω*,V)=0,即C*=0.524 nF,当I=0.008 A 时,满足C＞C*电路才会产生振荡,C*为该电路振荡的Hopf 分岔点.

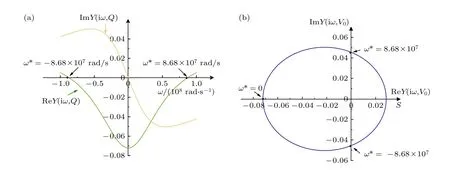
图5 (a) I=0.008 A 时的实部虚部的频率响应;(b) 奈奎斯特图Fig.5.(a) Frequency responses of the real and imaginary parts at I=0.008 A;(b) Nyquist plot.

3 基于NbOx 忆阻器的二阶振荡器

根据上述分析,由直流电流源、LAM 和补偿电容器一起构成的二阶振荡电路如图6 所示.其中Cp为器件本身的寄生电容,电容值在100 pF左右[29],由于本文所采用的电容C取值为20 nF,远大于器件自身的电容效应,因此在电路分析时该器件的电容效应可以忽略.基于基尔霍夫定律和电路元件的伏安关系,电路的状态方程可以表示为

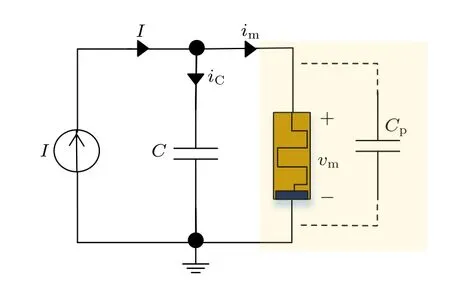
图6 二阶振荡电路Fig.6.Second-order oscillator circuit.

3.1 Jacobian 矩阵的特征根

除了采用NbOx忆阻器小信号导纳函数的频率响应来确定满足二阶电路振荡条件外,还可以通过计算平衡点处雅可比矩阵特征根来判断该平衡点的稳定性,进而确定Hopf 分岔点.当输入的直流电流激励I=0.008 A 时,S 型LAM 的工作点为Q(0.30032 V,0.008 A),利用Jacobian 矩阵的特征值来分析在该工作点处产生振荡的电容取值范围.首先将电路的状态微分方程式设置为0,可以得到振荡系统的平衡点为(2317.136 K,0.1767 V).基于(16)式,二阶振荡电路的Jacobian 矩阵为

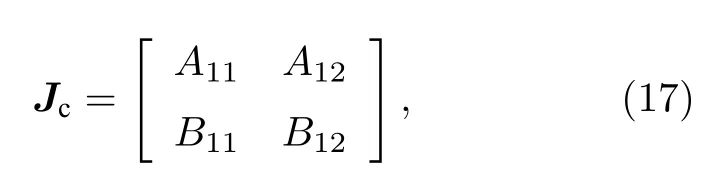
其中矩阵的元素分别为

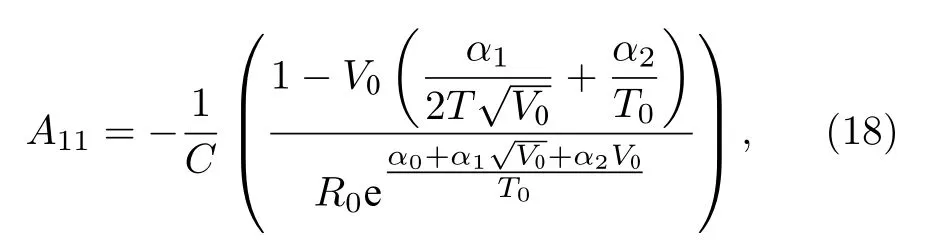
采用MATLAB 进行数值仿真分析,得到(17)式的特征根λ1和λ2在0.042 nF ＜C＜ 10 nF范围内的轨迹如图7 所示,蓝色和红色曲线分别对应λ1和λ2的轨迹,箭头表示了电容增加时特征根的运动方向.Reλ＞ 0 的区域是二阶电路的振荡区域.从图中可以看出,在C=0.524 nF 处出现了一对复共轭特征根,这是Hopf 分岔点.在Hopf 分岔点的左侧,特征根的实部小于0,二阶电路趋于稳定平衡点,反之处于振荡状态.因此,该分析方法表明,如图6 所示的电路可在工作点Q(0.3003 V,0.008 A)处对C＞0.524 nF 产生振荡.

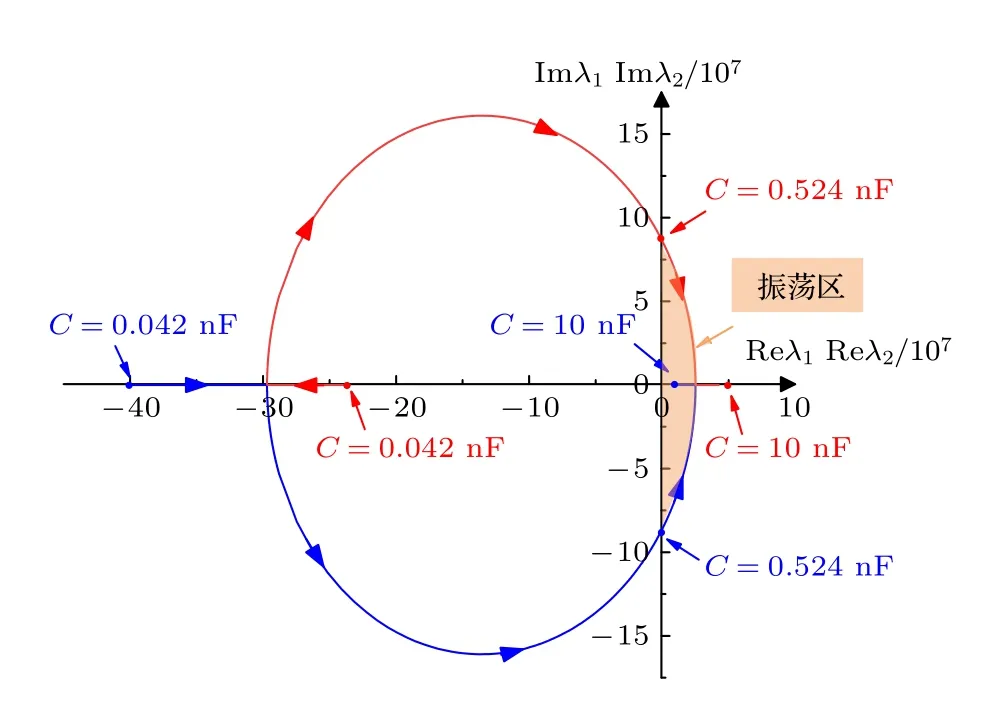
图7 雅可比矩阵的特征值在0.042 nF ＜ C ＜ 10 nF 范围内的变化Fig.7.Variations of the eigenvalues of the Jacobian matrix for 0.042 nF ＜ C ＜ 10 nF.

3.2 振荡行为分析

为了进一步验证基于NbOxLAM 的二阶振荡电路的行为,对二阶振荡电路进行了数值仿真.

当电容C=0.3 nF,小于分岔点处的电容值,初始状态为T(0)=0,vm(0)=0,电路的仿真结果如图8(a)所示,忆阻器的T-im相图如图8(b)所示.电压、电流和状态变量(温度T)的瞬态波形渐进收敛于平衡态VS=0.3003 V,TS=701.5887 K,IS=0.008 A.这与理论计算结果一致.同样,T-im平面上的相图轨迹也收敛于稳定点(701.5887 K,0.008 A).当电容值大于分叉点处的电容值时,如C=0.8 nF,初始条件不变,仿真结果如图8(c)所示.从图8(c)中可以看到,流过忆阻器的电流im的稳定瞬态振荡波形并非正弦信号,而是类似于神经元中的尖峰波形,图8(d)中T-im平面的相图轨迹为极限环,围绕稳定点(701.5887 K,0.008 A)运动.

图8 当I=0.008 A,C=0.3 nF 时,NbOx LAM 的二阶振荡器的仿真结果 (a)电压vm、状态变量T 和电流im 的瞬态波形;(b)稳定点的im-T 相图;当I=0.008 A,C=0.8 nF 时,NbOx LAM 的二阶振荡器的仿真结果:(c)电压vm、状态变量T 和电流im 的瞬态波形;(d) 振荡状态的im-T 相图Fig.8.Simulation results of the NbOx LAM second-order oscillator:(a) The transient waveforms of vm,T and im at I=0.008 A and C=0.3 nF;(b) the stable equilibrium on im-T phase plane at I=0.008 A and C=0.3 nF;(c) the transient waveforms of vm,T and im at I=0.008 A and C=0.8 nF;(d) the limit cycle on the im-T phase plane at I=0.008 A and C=0.8 nF.

3.3 激励对尖峰个数的影响规律

如2.1 节所提到的,若是直流电流I激励,则NbOx忆阻器可以稳定工作在该点,在NDR 区不同的工作点对应的二阶电路的振荡行为不同.本节主要研究在电流激励的情况下,其幅值对二阶电路振荡行为的影响.

在构成的二阶电路中,固定并联的电容值C=20 nF,输入直流信号,经过仿真分析,输入电流在(0.004 A,0.08 A)范围内增大,在一定时间内如10 µs,忆阻器电流的尖峰个数随之增加.图9(a)给出了电流激励为10,30 和50 mA 时,流过忆阻器电流的时域图,图9(b)给出了输入的电流激励I从0.012 A 增加到0.08 A 时,10 µs 内忆阻器电流尖峰输出个数n的情况.电流激励越大,二阶电路振荡的频率越大,这一结论也是第4 节将二阶电路构成神经元搭建尖峰神经网络进行模式识别的关键.

图9 (a) 输入的直流电流激励取10,30 和 50 mA 时,忆阻器电流的时域图;(b) 不同电流激励对应的尖峰数量关系图Fig.9.(a) The time-domain waveforms of im at different input DC current excitations of 10,30 and 50 mA;(b) the number of spikes corresponding to different current excitations.

4 用于模式识别的SNN

尖峰神经网络被称为第三代神经网络,旨在弥合神经科学和机器学习之间的差距,使用最适合生物神经元机制的模型来进行计算.

4.1 NbOx 忆阻器神经元电路

神经元通常具有多种不同的振荡模式[30],在NbOx忆阻器二阶振荡电路的基础上,设计了基于NbOx忆阻器的神经元电路,该电路在设计参数范围内具有相同的尖峰振荡模式,如图10 所示,其中基于AIST(AgInSbTe)材料的忆阻器用来模拟生物突触功能[31],电压信号Vik代表输入信号.NbOx忆阻器,电容以及运算放大器共同构成了神经元,Ineuron是突触阵列注入到神经元的电流,vneuron是神经元两端的电压,im是流过忆阻器的电流.从图10可以看出,所设计的神经元电路是在二阶振荡电路的基础上添加了运算放大器,目的是利用放大器的“虚短”和“虚断”特性,使得神经元的激励电流为

图10 基于NbOx 忆阻器的神经元电路Fig.10.Neuron circuit based on NbOx memristor.

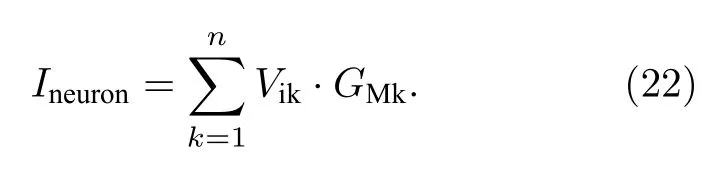
(22)式表明流过神经元的电流Ineuron受输入电压和突触权重的影响,GMk为第M列第k行对应的电导值.此外,神经元尖峰发放频率与Ineuron有关.因此,不同的输入信号和权重组合将会对应不同的尖峰频率,使得该神经元电路可用于构建SNN 并实现模式识别.

为了验证该神经元电路的有效性,令电容C取20 nF,输入电压Vi1=2 V,Vik=0 V (k=2,3,···n),对单一神经元电路进行仿真,仿真结果如图11 所示.图11(a)和图11(b)中,忆阻突触处于ON 状态(忆阻值取100 Ω,即突出权重较大)时,神经元的输入电流超出了神经元的阈值,成功激活神经元使其发放尖峰脉冲.图11(c)和图11(d)中,忆阻突触处于OFF 状态(忆阻值取100 kΩ,即突触权重较小)时,神经元输入电流很小,不足以激活输出神经元,即输出不产生电流尖峰.

图11 (a) 忆阻突触处于ON 状态时,Vi1 和vm 时域图;(b) 忆阻突触处于ON 状态时,im 时域图;(c) 忆阻突触处于OFF 状态时,Vi1 和vm 时域图;(d) 忆阻突触处于OFF 状态时,im 时域图Fig.11.(a) The time-domain waveforms of Vi1 and vm when the memristive synapse is at ON state;(b) the time-domain waveforms of im at ON state;(c) the time-domain waveforms of Vi1 and vm when the memristive synapse is at OFF state;(d) the timedomain waveforms of im at OFF state.

4.2 基于SNN 的数字模式识别

基于设计的NbOx忆阻器神经元电路,构建了一个25×10 的SNN 并用于数字模式识别.首先,确定每一种模式由5×5 像素块构成,如图12 所示,其中黑色和白色像素代表两种不同的输入电压取值,即黑色代表“1 V”,白色代表“0 V”.因此,输入信号的个数为5×5=25,待识别的模式为数字0—9,共10 种模式,输出神经元的个数为10,那么SNN 网络的大小为25×10.以数字“2”模式为例,输入神经元的电压序列为“01110000100111001 00001110”(“1”代表1 V,“0”代表0 V).

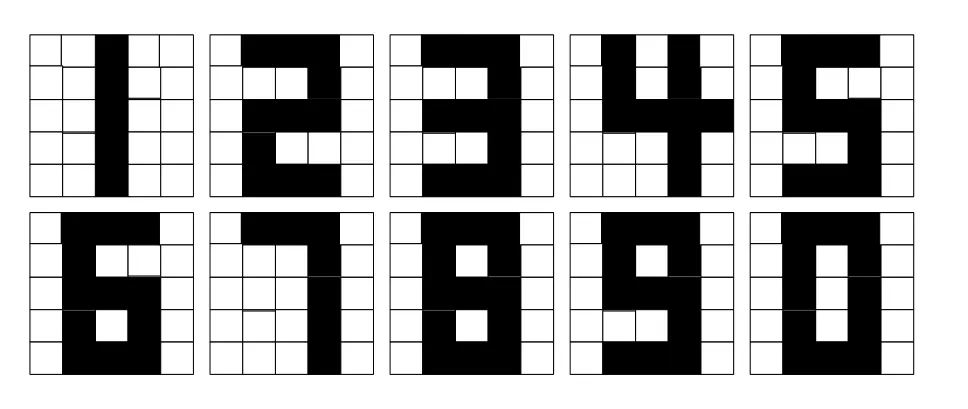
图12 5×5 的10 种数字模式Fig.12.10 digital patterns of 5×5.

基于输入神经元的电流越大,神经元的脉冲输出频率越大以及脉冲触发时间越早这一结论,本文将通过输出神经元的脉冲频率以及触发时间这两种编码方式实现模式识别.共有10 种数字模式,每一种模式由25 个像素块构成,则可以得到输入网络为10×25 的电压矩阵.为了有效地实现模式识别,采用了离线训练方法得到SNN 忆阻权重取值.训练方法较简单,即不同的模式输入下,仅有唯一一个的神经元获得的电流值最大,最大电流取值0.056 A,其余电流取0—0.04 A 中的任意值.当电流参数取0.004 A 以下时,神经元不会振荡,这样的设计可以有效地保证识别结果的准确性.例如:数字1 输入SNN 时,经过权重矩阵后输入到第一个输出神经元的电流是最大的,其余输出神经元的电流是小于最大值的随机值,依次类推,数字0 输入时,经过权重矩阵运算后输入至第10 个输出神经元的电流最大.

4.3 突触实现电路

在MATLAB 上求解了满足条件的25×10 的权重矩阵.原理方程由(23)式给出.i表示10 种模式中的每一个模式,j表示像素的数量,Vij表示每一种模式对应的输入电压向量,Wji表示突触阵列中的每一个电导值,Iii表示电压向量与突触权重矩阵运算之后得到注入神经元的电流值.

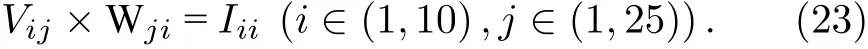
通过MATLAB 得到的满足识别条件的权重矩阵包含正、负权重.对于正的权重,通过设置忆阻器的输入电压,可以得到不同的正突触权值,而对于负的权重,则可以考虑构建两个忆阻器反向并联电路来实现.两个双极性忆阻器被设计成反向连接结构,它们之间阻值的差表示为突触的权量.通过施加外加激励,可以改变权重忆阻的值,从而得到正、负和零突触.采用AIST 忆阻器并联仿真了该电路,证明能够表示负、正和零的突触权重.图13给出了电压激励的突触电路[32],输入电压注入到两个忆阻器的连接点,运放A1和A2的输出电压分别为

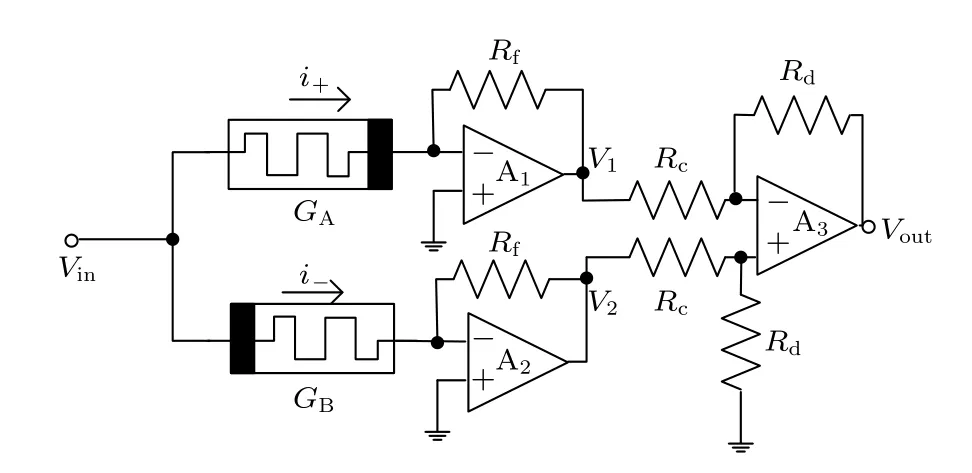
图13 电压突触电路实现Fig.13.Implementation of voltage synapse circuit.

其中支路电流信号表示为

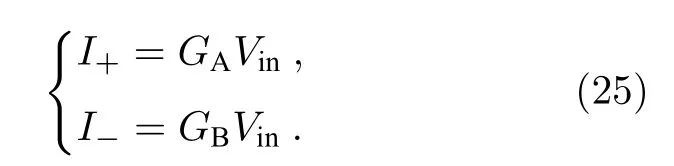
可以得到电压差方程为

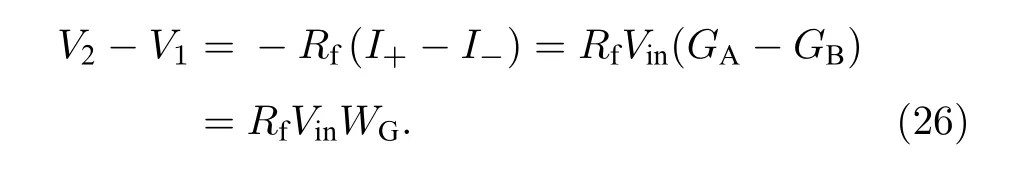
通过分析可以看出,突触权重表示为两个忆阻器的电导之差:

在上述突触计算中,所输入的电压和电流均是小于忆阻阈值,这样可以保证在计算时,忆阻器状态不会发生改变.反之,当所施加的信号大于阈值时,可以对突触权重进行编程,即当输入的是正向编程电压时,忆导值GA减小的同时,忆导值GB增大,导致突出权重电导减小.反之,当施加负电压信号时,突触权重电导增加.在上述编程过程中,由于两个忆阻器的极性是相反的,所以无论所施加的信号是正还是负,忆阻的变化始终是反向的,这样不但可以加速权重编程运算,而且在连续编程过程中可以始终保证得到正、零和负的突触权重,而无需提前的符号设定.

综上,构建了一个25×10 的尖峰神经网络,输入为10 种不同模式的编码电压,突触阵列由无源的忆阻器构成,输出神经元部分采用4.1 节提出的基于NbOx忆阻神经元,整体的SNN 结构如图14 所示.

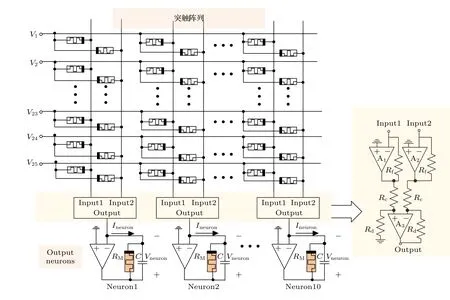
图14 由25×10 的突触阵列以及10 个输出神经元构成的尖峰神经网络Fig.14.A spiking neural network consisting of a 25×10 synaptic array and 10 output neurons.

4.4 识别结果

4.4.1 RC(Rated coded) SNN

RC SNN 是基于神经网络神经元的输出频率进行编码识别,以数字“2”输入网络时的识别结果进行说明.由4.1 节可知数字“2”对应的电压输入向量为:[0 1 1 1 0 0 0 0 1 0 0 1 1 1 0 0 0 0 1 0 0 1 1 1 0],单位是V,经过求得的权重矩阵运算,可得到经过运算放大器整合输入到每一个输出神经元的电流向量为[11.5 57.3 5.5 35.3 15.9 30.8 7.8 29.4 16.2 26.5],单位是mA,可以看到输入第二个神经元的电流最大.

图15(a)给出了数字2 输入网络时十个输出神经元中流过忆阻器的电流输出时域图,纵轴表示的是10 个输出神经元,从下到上分别表示神经元1 到10,对应输入模式1,2,···,0,可以观察到当模式2 输入网络时,输出神经元2 的电流频率最大.图15(b)给出了10 种模式输入网络时输出频率的结果,横坐标是10 种输入模式,纵坐标是10 个输出神经元,每一列表示一个输入模式对应的输出结果,不同的颜色代表不同大小的频率(右侧的颜色条说明了频率和颜色的对应关系),红色代表频率越大,蓝色代表频率越小.可以看出,每一种模式的输入都对应唯一一个输出神经元的电流脉冲频率最大,与4.2 节所提出的预期一致,通过判断哪一个输出神经元的脉冲频率最大即可判断输入的是哪一种模式.

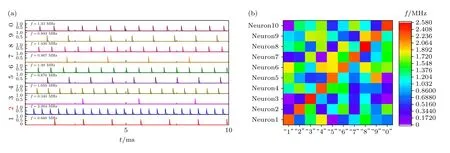
图15 (a) 数字2 输入尖峰神经网络,10 个输出神经元的电流im 输出时域图;(b) 10 种模式输入尖峰神经网络时各输出神经元输出电流频率的情况Fig.15.(a) The time-domain waveforms of im of 10 output neurons when“2”mode is input to SNN;(b) the output current frequencies of each output neuron when ten modes are input to the spiking neural network.

4.4.2 TC (Tempotral coded) SNN

TC SNN 是基于脉冲时间进行编码,这里提到的时间可以是首个脉冲的时间,也可以是整个输出脉冲的时间.本文采用的方案是根据输出神经元的首个脉冲的触发时间进行识别,可以利用触发器以及传输门来实现神经元单脉冲输出,如图16 所示,该方案可以大大地减小神经网络的能耗,获得更高的模式识别效率.电路实现原理:电路在初始状态时,D 触发器的Q端为0,与传输门的控制端相连,使传输门导通,神经元的输出作为D 触发器的时钟信号,当神经元触发了第一个脉冲时,D 触发器开始工作,Q从0 变为1,传输门关断,没有激励信号输入神经元,从而不再产生尖峰脉冲,达到了只产生单一脉冲的目的.图17 给出了在电容C取20 nF,输入电压为2 V,周期为10 µs 时的单脉冲实现结果以及没有使用这一方案时的结果对比.

图16 基于TC SNN 的神经元电路Fig.16.Neuron circuit based on TC SNN.

图17 (a) 单尖峰电路的仿真结果图;(b) 未应用单尖峰电路方案的仿真结果Fig.17.(a) The simulation results with the single-spike circuit;(b) the simulation results without the single-spike circuit.

与RC SNN 的识别一样,同样的输入电压矩阵和权重阵列,根据输入神经元电流不同,首先产生尖峰的时间不同来识别给定的10 种模式.以“2”模式的识别结果为例来说明TC SNN 的识别结果.图18(a)给出了“2”模式输入时10 个输出神经元首个脉冲输出的时域图,图18(b)给出了10 种模式输入神经网络时所有输出神经元的输出结果,紫色代表的时间最小,红色代表的时间最大.综上,当输入模式“1”时,神经元1 的输出脉冲时间最早,依此类推,当输入模式为“0”时,神经元10 的输出脉冲时间最早.即每种模式输入网络仅有一个输出神经元对应的脉冲触发时间最早,以此来达到一个识别的目的.

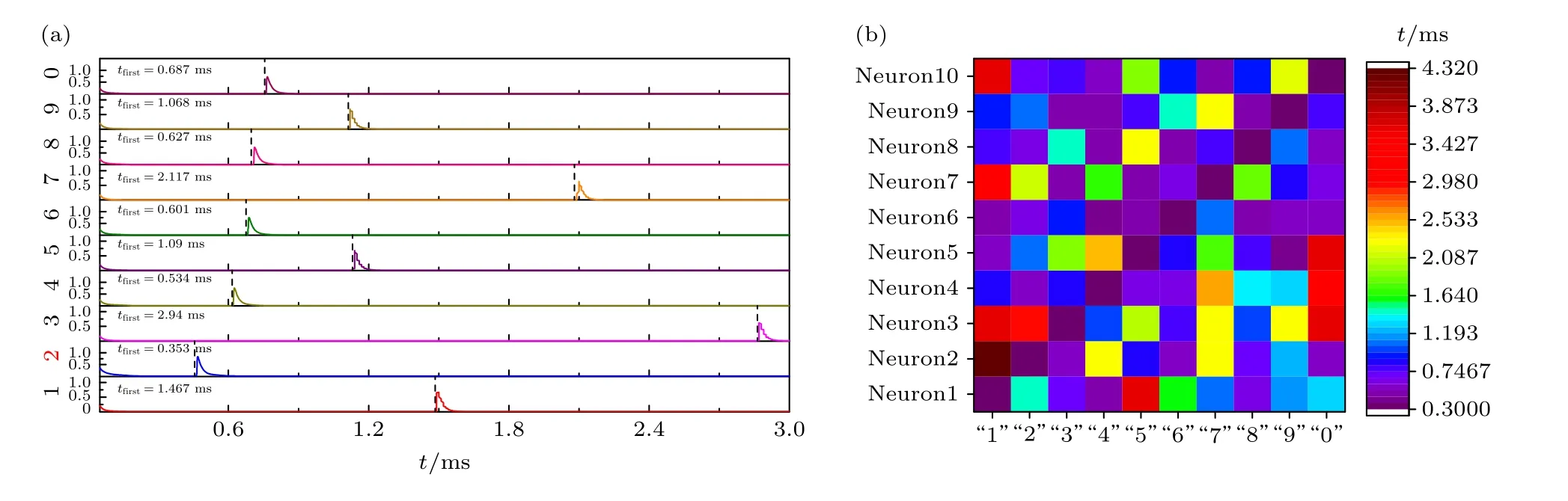
图18 (a)“2”模式输入SNN 时,10 个输出神经元的电流时域图;(b) 不同输入模式对应的神经元输出首个脉冲的时间Fig.18.(a) The time-domain waveforms of im of 10 output neurons when“2”mode is input to SNN;(b) the time of outputting the first pulse of neurons corresponding to different input modes.

5 总结

本文从电路理论的角度对NbOx-Mott 忆阻器进行了深入的电路理论研究,通过DCV-I验证了NbOx忆阻器的基本特性,小信号导纳的频域分析,二阶振荡电路的Hopf 分岔点分析等为NbOx忆阻器在周期振荡器,尖峰神经元中的应用提供了电路理论基础.此外,所设计的神经元电路由于放大器的引入具有输出频率可控性,使得基于NbOx忆阻器的神经元可以集成到脉冲神经网络中,实现了5×5 像素的10 种数字模式识别,提出了基于神经元输出电流的频率和脉冲触发时间两种识别方式,并给出了在LTspice 中的仿真结果,结果表明,所构建的25×10 的脉冲神经网络,可以通过观察输出神经元的忆阻器电流频率和首个脉冲的激发时间实现数字0—9 的识别,满足脉冲神经网络识别数字的预期目标.