马蹄形盾构机研制关键技术及工程应用

贾连辉，范 磊，冯 猛

(中铁工程装备集团有限公司，河南 郑州 450016)

目前，在隧道施工中，圆形隧道因其良好的受力结构形式，同时具有施工自动化程度高的优势，广泛应用于城市地铁隧道、引水隧道、地下管线等工程[1-2]。但圆形隧道同时也存在一定的缺点，隧道修建完成后，需要对开挖出的圆截面巷道底部进行预制仰拱块铺设等处理，以满足车辆运营使用等要求，但此过程无疑是对开挖空间的浪费[3-4]。近年来，矩形盾构隧道发展较为迅速，虽然在空间利用率方面表现更为突出，但其结构形式却限制了管片承受隧道深覆土压力的能力，对于开挖面大、覆土深的隧道，很难满足要求[5-6]。马蹄形断面隧道以其良好的结构受力形式(与矩形相比较)，较高的隧道断面利用率(较圆形提高15%以上)，结合了矩形与圆形隧道的技术优势，能够很好地满足双线铁路软岩深埋隧道的应用需求。

然而，马蹄形隧道多采用矿山法或明挖法施工，不仅安全性差、施工环境恶劣而且施工效率较低，仅为盾构法的1/3[7]。因此，为采用盾构法施工，研制马蹄形盾构机。本文概述马蹄形盾构机研制的关键技术，主要包括低扰动多刀盘多驱动协同开挖技术、多曲率管片拼装机技术、双螺旋输送机联合排渣技术、盾体设计及姿态控制技术等；同时分析马蹄形盾构机在工程应用过程中出现的问题，提出针对性的改进措施，并对改进效果进行验证。研制的马蹄形盾构机，实现了相关理论与核心技术的突破，成功应用于蒙华铁路白城隧道施工中。

1 依托工程概况

本文依托的蒙华铁路白城隧道项目位于陕西省靖边县内，隧道全长3 345 m，为时速120 km单洞双线电气化铁路隧道，隧道全段为直线段，纵坡为人字坡，坡度及坡长依次为4.5‰/1 935 m，-3‰/900 m，-11‰/510 m。最大埋深为81 m，洞身范围内地层主要为粉砂、细砂、砂质新黄土。隧道下穿包茂高速公路、靖黄公路、天然气管道、白城子供水管线。

白城隧道纵断面如图1所示，设计轮廓近似马蹄形，具有3个半径，4个圆心，上部为圆拱，下部稍扁，左右两翼下侧的圆弧直径较小，各圆弧相切，竖向最大高度为9 590 mm，横向最大宽度为10 540 mm。

图1 白城隧道纵断面图(单位：mm)

2 马蹄形盾构机研制关键技术

2.1 多刀盘多驱动协同开挖技术

2.1.1 刀盘组成及开挖方式

马蹄形盾构机刀盘开挖形式采用平行轴式9组刀盘布置方案，3个前刀盘，6个后刀盘，前后错开，开挖覆盖率可以达到90%以上，刀盘结构图及编号如图2所示，其中2—7号大刀盘由5根刀梁组成，1号、8号及9号刀盘由3根刀梁组成。组合式旋转多刀盘的开挖特性决定着开挖盲区的存在，因此在该位置通过布置高压水冲刷、渣土改良通道，以及采取其他辅助措施，对开挖盲区进行渣土处理，在盾体周边通过布置盾体切刀，保证开挖断面的尺寸[8]。

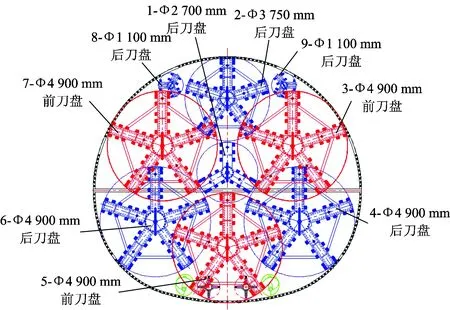
图2 刀盘组成及编号

2.1.2 小刀盘驱动扭矩系数

盾构主驱动的额定扭矩计算，可参照日本盾构隧道标准规范建议的主驱动额定扭矩计算公式[9]，即

T=αD3

(1)

其中，

α=α1α2α3

(2)

式中：T为刀盘额定扭矩；α为刀盘扭矩系数；D为刀盘直径；α1，α2，α3分别为与刀盘支承方式、土质条件、平衡形式相关的扭矩系数。

分析大量的工程应用数据可知，式(2)对直径3 m及其以上的刀盘较为适用，而对直径3 m以下刀盘(以下简称为小刀盘)则不适用，往往出现驱动扭矩不足，或者驱动扭矩过大导致电机跳停的现象。为此，目前在进行小刀盘额定扭矩设计时，多在式(2)的基础上再增加1个安全系数，但安全系数的值多依据经验给出，计算结果还是会有误差，并且缺少理论依据。

针对该问题，选取以往的顶管、盾构等大量隧道掘进机施工时的刀盘直径与扭矩系数，采用OriginPro软件进行离散点数据回归分析，如图3所示。

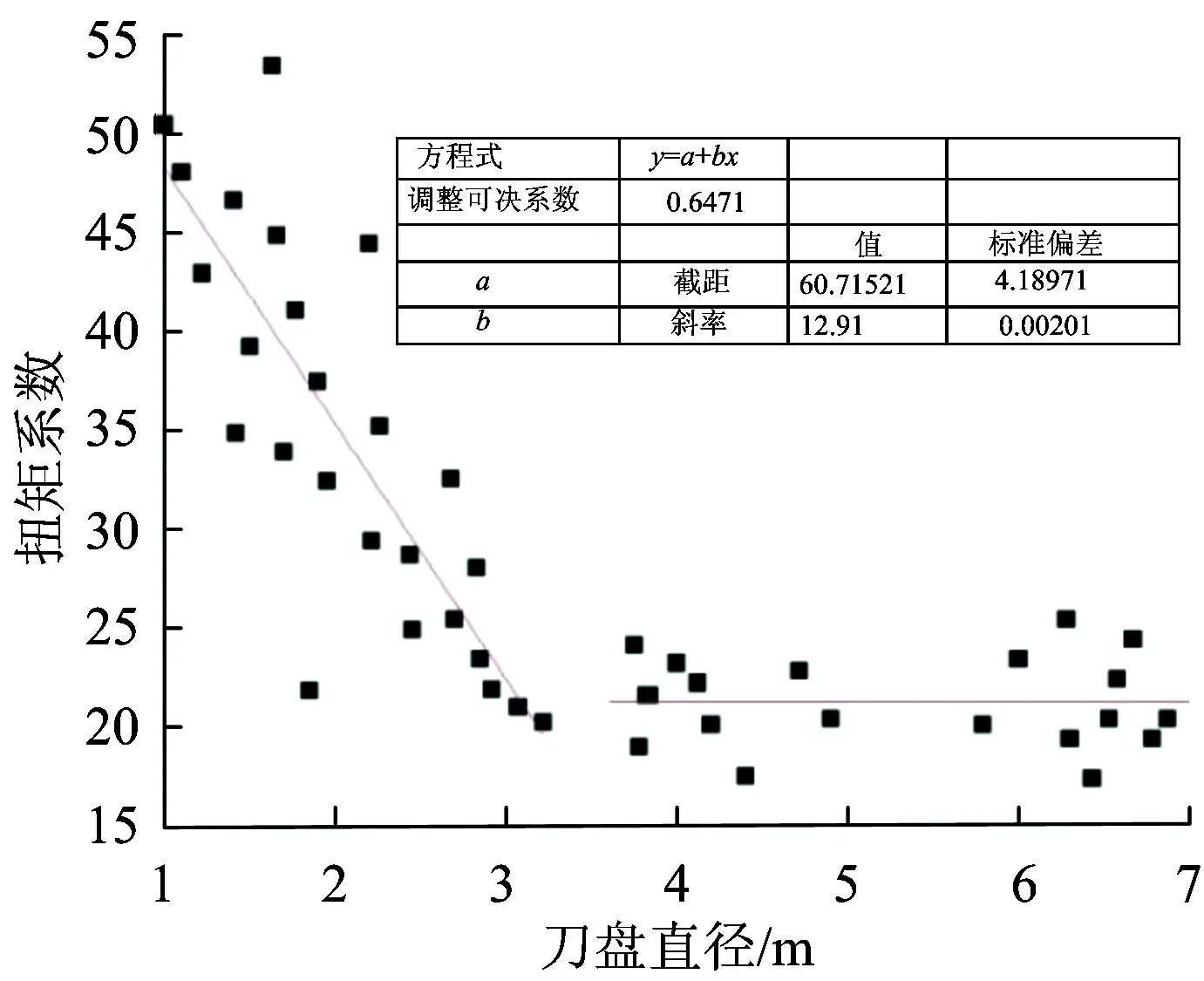
图3 不同刀盘直径时扭矩系数离散点的回归分析

从图3可以看出：直径3 m及其以上刀盘仍符合式(2)扭矩系数计算公式，均在20左右；而小刀盘扭矩系数与刀盘直径呈负相关关系。

对小刀盘，其回归方程为

α=-12.91D+60.72

(3)

式(3)在一定程度上反映了扭矩系数α与刀盘直径的相关关系，但该方程并未反映α1，α2，α3对扭矩系数α的影响，若以此作为小直径刀盘扭矩系数的计算方法，误差较大。因此定义由式(2)计算得到的扭矩系数为传统扭矩系数α传统，即α传统=α1α2α3；小刀盘直径对扭矩系数的影响系数为α小。则小刀盘扭矩系数α由两部分组成，即

α=α传统+α小

(4)

针对小刀盘，为提高回归方程精度，在消除传统扭矩系数α传统影响的条件下，仅对α小进行回归分析，如图4所示。

得到的回归方程为

α小=-14.22D+41.6

(5)

将式(5)和α传统=α1α2α3带入式(4)，得小刀盘驱动扭矩系数计算公式为

α=α小+α传统

=-14.22D+41.6+α1α2α3

(6)

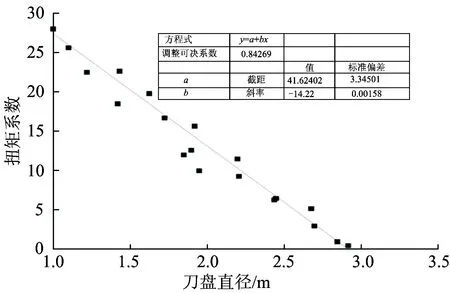
图4 消除传统扭矩系数影响后扭矩系数离散点的回归分析

对于D=2 700 mm和D=1 100 mm的2个小刀盘，分别利用式(6)、式(2)计算小刀盘驱动扭矩系数，再都利用式(1)计算驱动额定扭矩，结果见表1，并将其与实际工程中正常掘进下的驱动扭矩对比进行对比。结果发现：利用式(2)计算得到的驱动额定扭矩较小，工程应用中会出现扭矩不足等现象；利用式(6)计算得到的驱动额定扭矩更为合理，既满足实际工程中的需要，且预留了一定的安全系数。

表1 驱动扭矩对比表

2.2 马蹄形多曲率管片拼装技术

2.2.1 管片拼装方式

综合考虑管片的制作、防水、运输、拼装和结构受力等因素[10-11]，将管片分为8块。采用错缝拼装方式，管片环分为偶数环和奇数环相互交叉，并且奇数环和偶数环的错缝位置为轴对称，即所有奇数环的纵缝位置相同，偶数环的纵缝位置相同，如图5所示。管片拼装顺序如图6所示。

2.2.2 管片拼装机结构设计

区别于常规圆形管片，马蹄形管片非中心对称，管片圆弧直径有3种且尺寸差距较大，每个管片形状和尺寸均不一致，重心偏置，最大管片重量达10 t。使用常规机械式举升钳，最大起重量为6 t，无法满足要求，而真空吸盘式抓举头无法抓取多种圆弧的管片，且异形管片拼装动作复杂[12-15]。

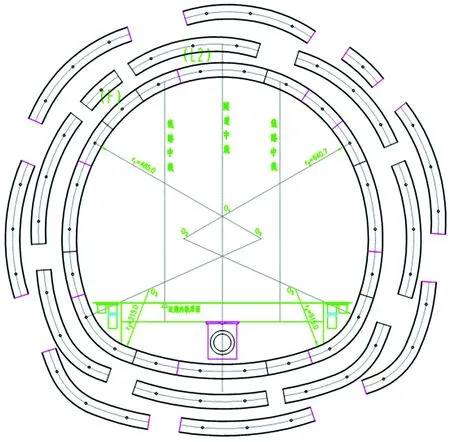
图5 管片错缝拼装图

图6 管片拼装顺序

为此，设计了1种适用多曲率管片的拼装机。

多自由度管片拼装机如图7(a)所示，其主要由回转机构、伸缩机构和抓举头组成，能够完成锁紧、升降、平移、回转、俯仰、扭转和偏转7种动作。其中，回转机构主要由回转动力系统、回转架、支重轮等组成。回转架为圆形结构，通过动力系统带动绕Z轴旋转，由支重轮提供支撑与盾体连接，由于管片较重，带载运转时偏载较大，在回转架上部布置了平衡负载的配重块。伸缩机构通过主梁与回转架连接，由油缸带动伸缩导向柱上下移动。

抓举头如图7(b)所示，通过平移油缸实现管片在Z′方向平移，通过俯仰油缸实现管片绕Z′方向旋转，通过提升油缸提升管片，2个起吊螺钉设计及4个锁紧油缸满足变曲率大重量管片的抓取及锁紧，扭转油缸可实现管片绕y′方向旋转。如图7(c)所示，提升油缸端部与起吊平衡梁铰接，在管片提升锁紧过程中起吊平衡梁可自适应不同曲率的管片，调整起吊平衡梁的角度，实现马蹄形管片的抓取。

2.3 双螺旋输送机联合排渣技术

超大断面马蹄形盾构机横向跨度大，开挖量大，土仓存在渣土滞排问题，同时土仓左右土压力平衡控制难度高，对排渣系统的排渣能力及均衡性提出了新要求，因此，设计了有2台螺旋输送机联合出渣的排渣系统，如图8(a)所示。

由于2个螺旋输送机同时对土仓渣土进行排渣，每个螺旋机的速度都会影响土仓压力的平衡，因此采用Fluent软件对土仓渣土流场压力进行分析。针对该项目的地质，在典型土层试样中使用水、泡沫、膨润土作为添加剂进行渣土改良试验，通过坍落度试验、透水性试验等进行对比[16]，得到渣土改良的最佳方案，使用注入率为15%的泡沫时，满足土体流塑性状态要求。改良后的土体密度为1 580 kg·m-3，屈服黏度为670 Pa·s，静切应力为12 kPa，稠度指数为1，幂律指数为1.1，刀盘转速取1 r·min-1，计算结果如图8(b)所示，结果表明左右螺旋输送机进渣口渣土流动速度不相同，刀盘转向会造成左右螺旋出渣口存在压差。为了提高土仓全断面压力均衡性，对土仓压力及双螺旋输送机的压力进行实时监控并反馈至上位机，实现双螺旋的实时控制，消除双螺旋出渣的压力差，其控制策略如图8(c)所示。

图7 管片拼装机及其抓举头的结构图

图8 双螺旋输送机的结构图及其工作原理图

2.4 马蹄形盾体设计及姿态控制

2.4.1 马蹄形盾体设计

马蹄形盾体的上部为圆拱，掘进时能够形成天然卸荷拱，周向载荷分布与常规圆形盾构类似[17]。但马蹄形盾构机采用多刀盘开挖形式，轴向载荷分布差异较大。因此，考虑成本和运输因素，在满足强度与刚度的要求下，需尽量减小盾体的重量。

设计的马蹄形盾体如图9所示，主要包括前盾、中盾和尾盾3部分，这3部分都是马蹄状筒体，前盾和与之焊在一起的前隔板用来支撑刀盘驱动。前盾和中盾通过法兰以螺栓连接，中盾和尾盾采用现场焊接，尾盾末端装有密封用的盾尾刷。

为克服大型盾构软土及软岩地层卡盾问题，对盾体进行了梭式结构针对性设计，中盾较尾盾、前盾较中盾的外轮廓尺寸依次阶梯增大15 mm。

图9 马蹄形盾体示意图

2.4.2 姿态控制

因白城隧道位于直线段，故盾构机未设计主动铰接，盾构机调向是依靠各个顶推油缸的压力差实现的。一般而言，无铰接的盾构机转弯是通过一系列的折线代替曲线实现的[18]。在盾体总体长度L、盾构机允许的水平偏移Δ和每次掘进行程S已知的前提下，无铰接盾构机允许的转弯半径R为

(7)

根据马蹄形盾构机的设计参数及式(7)，得到该马蹄形盾构机的最小转弯半径约为800 m。此外，根据盾尾间隙得到最大偏转角为0.72°。

由于推进油缸主动调向能力有限，因此在曲线段施工时，盾构机需设计铰接机构，增加转弯能力和姿态控制能力，同时需配合特制的转弯环管片，通过管片的楔形量进行隧道的转弯。常规圆形掘进机在发生滚转时，不会对隧道成型质量造成影响，通过刀盘的反转即可进行校正。而对于马蹄形盾构机来说，由于隧道非中心对称，在其推进过程中，土压的不均匀及地质的变化，很容易造成盾构机发生水平轴线偏转或滚转，导致隧道形状改变，因此，应严格控制盾构机的姿态。

因此，在盾壳上设计有水平倾角传感器，实时监测盾体滚转姿态，并设有预报警系统。每个刀盘的旋转速度及方向都可调，从而实现纠滚。螺旋机转速可实现无级调速，控制土仓左、右压力，实现辅助纠滚。

在盾体发生微小滚转时，一般通过控制刀盘旋转方向，通过刀盘的反扭矩提供盾体反滚转扭矩；而发生较大角度滚转时，通过往盾体周向加压同时配合配重块进行强制纠滚。在实际应用过程中，应尽量避免盾体滚转角度过大，要求盾构的姿态控制做到实时测量、及时纠正[19]。

3 工程应用及优化

3.1 应用基本情况

研制的马蹄形盾构机整机在2016年7月下线，用于蒙华铁路白城隧道施工，在2016年11月11日始发掘进，2018年1月26日完全贯通。总体上，在整个施工过程中掘进整体性能良好，最高日掘进19.2 m(12环)，最高月掘进308.8 m，满足安全、快速、环保施工的要求。

施工过程中，管片拼装系统能很好地适应马蹄形断面管片的拼装，隧道成型质量较高，管片错台控制在3 mm以内。管片拼装平均用时40 min，实现了拼装的安全、高效。

3.2 施工中出现的问题及设备优化

3.2.1 积渣问题及解决方案

在施工过程中，出现了排渣不顺、螺旋输送机空转的问题，平均每天掘进1～2环，土仓内压力变化较大，影响了施工效率及地表沉降。经过停机检查发现，由于项目地质存在湿陷性黄土，遇水后在刀盘切削力作用下易大块坍塌，多刀盘前后布置形式为避免干涉存在搅拌盲区，大块渣土在土仓底部搅拌盲区位置容易堆积，如图10所示，形成较为硬实的土拱，影响渣土流动，导致排渣不畅。

图10 防积渣措施布置图

针对该问题，研究提出了以下2个防积渣措施，使出渣较为顺利。

措施1：利用高压水射流技术对渣土进行切割冲刷。

射流是一种孔口为狭缝出流的流动现象，具有很强的脉动性。为了使喷嘴的冲刷面积达到最大化且保证冲刷流速，采用FLUENT软件模拟2种开口角度喷嘴的高压水射流速度，研究喷嘴开口角度与冲刷效果之间的关系。

建立喷嘴的三维模型，使用Gambit进行网格划分，导入Fluent软件，计算得到水射流速度云图，如图11和图12所示，可见2种开口角度喷嘴的水射流速度分布规律相似，即水射流的流速在离开喷嘴处迅速增大，达到最大值，离开出口后迅速减小，相同水射流压力下，喷嘴出口越大，流速及动压衰减越快，喷射面积越大。为了增大冲刷面积，选择增大喷嘴开口及水泵压力的方案，确定喷嘴开口角度为170°，此时喷嘴开口宽度为10 mm，水射流起到水刀的效果，通过可伸缩装置增大冲刷范围。

在土仓隔板底部设置可伸缩式高压水射流冲刷装置2套，在搅拌盲区位置设置多个高压水射流喷口(安装位置见图14)。该装置的结构如图13所示，高压冲洗喷嘴与喷管连接，通过油缸带动喷管前后伸缩，油缸通过支撑板和后座板固定，油缸与喷管铰接，密封组件内置于密封座内，通过压盖可调节密封效果。可伸缩式高压水射流冲刷装置冲刷范围较大，可有效解决土仓底部积渣的问题，提高渣土流动性。

图11 喷嘴开口角度90°时水射流速度的分布云图

图12 喷嘴开口角度170°时水射流速度的分布云图

图13 可伸缩式高压水射流冲刷装置

措施2：在螺旋输送机上部设置2个推土器装置，防止土仓内土拱的形成，保证顺利排渣。

推土器装置结构如图14所示，密封座通过螺栓连接在土仓隔板上，推土杆穿过密封座深入土仓与推土板方形卡槽及螺栓连接；推土器与土仓隔板成一定夹角向后上方倾斜，倾斜角度大于螺旋输送机倾斜角度。推土板(如图15所示)的迎土面焊接有切土条，便于推进切土；推土板的背土面做大倒角处理，减小回收分土阻力。在推土器的推动下渣土能够向下落入螺旋输送机出渣区域或搅拌器搅拌区域，破坏土拱。

图14 推土器装置

图15 推土板结构

3.2.2 顶推力过大等问题及其解决方案

1)问题分析

在工程试验过程中，掘进第1045环时，出现下部3个大刀盘扭矩几乎为零，盾构机顶推力达到90 000 kN以上的情况，且姿态出现上浮现象，纠偏困难。分析发现，出现该现象的主要原因是掘进地质开始发生改变，开挖面下部为黏质老黄土夹姜石，姜石块无侧限抗压强度为2 MPa，中部为黏质老黄土，地质条件为上软下硬。经现场开仓检查发现，软岩地质围岩对盾体产生强烈的挤压，尤其是底部围岩对盾体产生较大的迎面阻力及摩擦阻力。

2)解决方案

刘泉声[20]等基于Hoek-Brown准则，研究了软岩无支护条件下隧道径向位移量ur沿掘进轴向方向(y方向)变化规律，给出的计算公式为

(8)

其中，

(9)

(10)

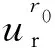
设超挖产生的围岩与盾体之间的间隙为ΔR，当ur(y)-ur(0)≥ΔR时，围岩与盾体开始接触，产生相互作用力，设距离开挖面距离为y处的盾体变形为us(y)，则

us(y)=ur(y)-ur(0)-ΔR

(11)

盾构机掘进时，盾体与围岩之间的作用力p(y)为

p(y)=Ksus(y)

=Ks[ur(y)-ur(0)-ΔR]

(12)

式中：Ks为盾体刚度。

考虑到前盾、中盾、尾盾成阶梯型结构，则盾体受到的摩擦阻力Rf等于围岩压力pi(y)对盾体表面的积分加上盾体重量引起的摩擦阻力，即

(13)

式中：R1，R2，R3依次为前、中、尾盾半径；μ为盾体与围岩之间的摩擦系数；ΔR1，ΔR2，ΔR3依次为超挖产生的围岩与前、中、尾盾之间的间隙；W1，W2，W3依次为前、中、尾盾盾体重量；L1，L2，L3依次为前、中、尾盾长度，L0=0。

由式(13)可知，通过加大底部刀盘开挖直径，可以增大底部的超挖量ΔR，减小摩擦阻力，此外，可以减小盾体切刀切削土体造成的迎面阻力，减小推力，辅助盾体进行向下纠偏，调整盾构机姿态。

根据计算结果采取的总体改进方案是：增大4号、5号、6号刀盘直径(由原来的Φ4 900 mm增大到Φ5 500 mm)，同时，由于刀盘干涉问题，将中部1号刀盘(Φ2 700 mm)刀盘直径缩小，开挖区域变化如图16所示；为了避免超挖造成的地表沉降，增加同步注浆量，减小土体扰动，加长4号、5号、6号刀盘的刀梁，在刀梁上焊接刀具，此外将5号刀盘中心的斜梁及搅拌棒割除，焊接新斜梁，避免与4号、6号干涉，如图17所示。

3)改造后刀盘静力学分析

为了确认刀盘改造完成后其强度刚度满足要求，利用ANSYS Workbench对改造后的5号刀盘进行静力学仿真。刀盘主要承受前方土体传递来的土压力(根据设计规范，一般取土压力为50 T·m-2)[21]，对刀盘前面板施加均布载荷，刀盘结构件承受扭矩根据设计最大扭矩计算，取3 044 kN·m，约束刀盘筒体，优化前、后刀盘的变形云图、应力云图分别如图18和图19所示。

图16 刀盘改进后开挖区域变化示意图

图17 5号刀盘改造示意图

图18 5号刀盘改造前的变形云图和应力云图

图19 5号刀盘改造后的变形云图和应力云图

仿真结果对比见表2，可以看到，改造后的结构刚度变弱，变形量变大，但最大应力小于材料的许用应力295 MPa，因此，可以确认改造后的刀盘满足刚度设计要求。

表2 5号刀盘改造前后刚度比较

4)刀盘改造前后盾构机的顶推力和扭矩

刀盘改造前后盾构机的扭矩变化曲线如图20所示。由图可知：刀盘改造后，扭矩由650 kN·m增加到1 250 kN·m，这是由于刀盘直径增大使得开挖面积增大，加上地质条件的变化引起的。5号刀盘设计额定扭矩为3 044 kN·m，仍能完全满足刀盘改造后的使用要求。

刀盘改造前后盾构机的顶推力变化曲线如图21所示。由图可知：刀盘改造前，在1 045环之前，平均顶推力为72 000 kN，1 045环后顶推力增加至85 000 kN左右，最大达到90 000 kN以上；刀盘改造后，顶推力降低为6 000 kN，相比优化前顶推力下降2 500 kN。同时，盾体切刀切土的长度减少10 340 mm，开挖盲区减小，在控制地表沉降的同时，优化效果明显，且改造后盾体姿态控制良好。

图20 5号刀盘改造前后扭矩变化曲线

图21 刀盘改造前后的顶推力变化曲线

4 结论与展望

研制了马蹄形盾构机，关键技术主要包括低扰动多刀盘多驱动协同开挖技术、多曲率管片拼装技术、双螺旋输送机联合排渣技术、马蹄形盾体设计及姿态控制技术等。并成功应用于蒙华铁路白城隧道施工。

(1)提出了低扰动多刀盘多驱动协同开挖技术。基于回归分析方法，揭示了小刀盘扭矩系数随刀盘直径的变化规律，推导了小刀盘扭矩系数计算公式。

(2)首次研究了马蹄形管片分块方式，设计了1种多自由度变曲率管片拼装机，通过拼装机的7种动作解决了变曲率、大重量管片的拼装难题，可实现马蹄形管片的高效精确拼装。

(3)针对超大马蹄形开挖断面，研究了双螺旋输送机联合出渣技术，基于Fluent仿真分析对开挖面进行流场仿真，通过压力监控及反馈实现了双螺旋输送机土仓压力实时控制。

(4)针对卡盾问题，设计了梭式盾体结构，给出了无铰接盾构机最小转弯半径计算方法，并提出了相应的纠滚措施。

(5)在马蹄形盾构机实际施工过程中，对出现的特殊地质条件导致的排渣不畅问题，提出了利用高压水射流技术冲刷、在螺旋输送机上部设置推土器装置的改进措施，改造后出渣较为顺畅；对顶推力过大等问题进行分析，采用增大3个底部刀盘直径等的改进措施。改进后设备各系统运行良好，为后续马蹄形盾构机的设计及应用提供借鉴。

(6)马蹄形盾构机的研制及应用，解决了异形盾构多项核心技术难题，为世界上首次应用于山岭铁路双线隧道，项目的成功实施为马蹄形断面隧道使用盾构法施工成为可能，实现了安全、快速、环保施工，开创了超大马蹄形隧道盾构机施工一次开挖成型的先河，为大型山岭铁路双线隧道施工起到引领示范作用。