合肥地铁某盾构区间土仓压力理论计算

胡梦涛，李大华，张自光

（安徽建筑大学 土木工程学院，安徽 合肥 230601）

1 研究背景

随着城市化的发展，城市人口和规模不断地增加，地面交通面临着巨大的压力。地下轨道作为缓解城市交通压力最好的方法之一，被越来越多地使用。在地下轨道交通修建中，盾构隧道施工法是最为常见的方法。土压平衡盾构机在施工过程中依靠其盾构外壳支撑围岩，并保护刀盘，对隧道前方土体进行开挖。经刀盘切割打碎后的土体，一部分留在刀盘后方的密封土仓内，用以维持开挖面稳定，最大程度降低对前方土体的扰动，减小盾构施工中所产生的地表沉降以及对周围建筑物的影响；另一部分土体通过土仓后方的螺旋机输送排出。因此，确定土仓压力在实际工程中具有重要的价值。

关于土仓压力大小的计算，国内外学者进行了大量研究，获得了丰富的成果。如Janssen & Koenen通过建立楔形三维模型，计算出了盾构掌子面的极限支护压力；德国的M.Herrenknetcht通过对隧道滑动面破坏形状的研究，提出了极限支护压力计算方法[1]。此外，王洪新等[2]对盾构机进行了力学分析，并建立了土仓压力控制理论。高鹏兴等[3]对土仓压力计算方法进行了研究，提出了一个适用于盾构隧道穿越弱透水地层的土仓压力计算模型。徐天生等[4]对于土仓压力引起的地表沉降进行了分析，总结了地表的沉降规律。

虽然科研工作者们对于土仓压力的计算已进行了大量的研究，为仓内压力设置提供了一定的参考依据，但已有研究多数仅从土力学的角度出发，通过对开挖面的变形与破坏进行分析，简单地将开挖面极限支护压力等同于土仓压力，忽略了开挖过程中盾构机的工作原理[5-6]，未能较好地反映出盾构机在施工中超挖、欠挖等工作状态，存在一定的局限性。因此，本文将以现有理论为基础，侧重于对盾构机工作原理的分析，从而进一步探究土仓压力的计算方法，为日后类似工程土仓压力设置提供参考依据。

2 工程概况

2.1 工程位置概况

本研究选定的地铁盾构区间为合肥地铁四号线丰乐河路站—玉兰大道站，隧道为两条单洞、单线圆形隧道。区间右线设计起止里程为YK8+ 718.072—YK10+188.850，右线区间长度为1 470.77 m。丰乐河路站—玉兰大道站区间线路主要位于习友路下方。隧道平面最小曲面半径为500 m，线间距为9.1～17.5 m，区间隧道覆土厚度为9.85～19.85 m，最大纵坡为28%。

2.2 工程地质条件

此区间隧道穿越的地层，为洞顶部分以强风化砂质泥岩⑨12层为主，局部有零星硬塑状态的黏土和中风化砂质泥岩⑨13层；洞身主要为强风化砂质泥岩⑨12层和中风化砂质泥岩⑨13层，洞底主要为中风化砂质泥岩⑨13层。其中，强风化砂质泥岩⑨12层为基岩裂隙水含水层。掘进区域内地层的物理力学特性具体见表1。

表1 掘进区域内地层的物理力学特性Table 1 Physical and mechanical properties of stratum in an excavation area

3 盾构极限支护压力计算

3.1 理论方法

土压平衡盾构机在掘进过程中，不可避免地会对隧道周围土体产生扰动，导致土体初始应力平衡被破坏。隧道前方土体在土压力、地下水压力以及地表均布荷载的作用下产生侧向压力，使得前方开挖土体发生位移，地表出现沉降或隆起。随着开挖面土体位移的增加，土体的抗剪强度充分发挥，最终达到极限平衡状态。此时，需要依靠掌子面提供足够的支护压力，以保持开挖面稳定。支护压力主要由盾构机前方的面板以及面板后的土仓压力共同提供。当支护压力过小时，土体向隧道内倾斜，地面发生沉降；当支护压力过大时，掌子面前方土体受到挤压，地面将产生一定的隆起，过大的沉降或隆起都会对地面建筑以及盾构施工安全产生极大影响。因此，支护压力的合理设置对整个盾构施工过程具有重要意义。因此，拟通过对开挖面极限支护压力的研究，结合盾构机在开挖过程中的工作原理，进而推导出改进后的土仓压力的理论计算公式。

目前，国内外对于盾构极限支护压力的计算公式主要有两种：一是德国工业标准DIN4085，二是Janssen&Koenen滑动土三维楔型模型。

3.2 德国工业标准DIN4085

德国工业标准DIN4085计算方法中，为了提高支护压力的计算精确度，将掌子面所在土层数目分为若干个薄层，并且依据隧道埋深的比值设置了形状系数u。当隧道埋深比值越大时，形状系数u值越小，土体自身承受的力增加，盾构机掌子面所需提供的支护压力越小；反之，当隧道埋深比值越小时，掌子面所需提供的支护压力越大。考虑到计算结果的安全性，将土的黏聚力系数ach设为均值1，当掌子面处在非黏性土地层时，ach值为0。通过计算，可得每一个薄层的上部和底部的侧向土压力，最终求出开挖面整体所需要的支护压力P。具体的计算公式如下：

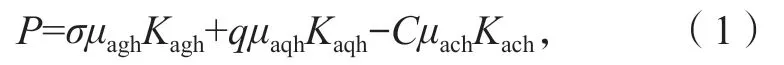
式中：μagh、μaqh、μach分别为土体自重、附加压力和土体黏聚力的形状系数；

σ为竖直土压强；

q为地面附加压力；

C为土体黏聚力。

Kagh、Kaqh、Kach分别为主动土的侧向压力系数、连续荷载下的侧向压力系数、黏聚力的侧向压力系数，且

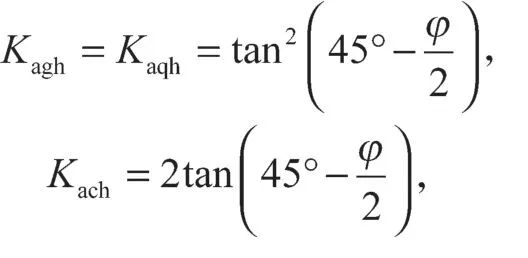
其中φ为土体内摩擦角。

3.3 三维楔形模型理论

Janssen&Koenen滑动土三维楔形模型是在Horn筒仓模型理论基础上进行改进得出的。模型由开挖面前方的楔形体与上部的立方体两部分组成。随着楔形体在开挖过程中产生位移，上部的立方体发生松动，在抗剪切力与黏聚力的作用下形成压力拱，使得上部土压力降低。三维楔形模型示意图见图1。

图1 三维楔形模型示意图Fig.1 Schematic diagram of 3D wedge model

沿隧道机掘进方向的支护压力计算式如下：

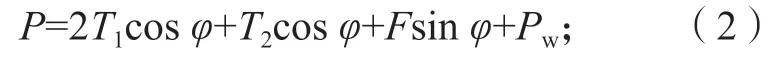
沿隧道竖直方向的支护压力计算式如下：

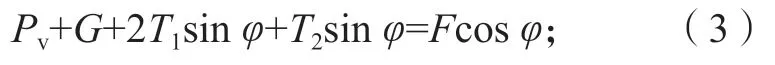
联立式（2）（3）可得：

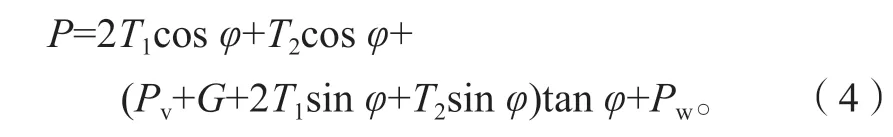
式（2）～（4）中：T1、T2分别为楔形体两侧和底部的摩擦阻力；

F为土体对楔形体的支持力；

Pv为上部柱体竖向压力；

G为楔型体重力；

Pw为侧向水压力。

4 土仓压力计算

4.1 土仓压力计算难点

土仓压力的理论计算难点主要有两个方面：

1）隧道上覆土压力在土仓压力计算过程中会直接影响支护压力，因此确定覆土压力的大小具有重要的意义。常见的上覆土压力计算公式有朗肯土压力、太沙基松动土压力公式。前者不考虑滑动块周围土体对其摩擦力的影响，一般适用于埋深比（H/D）小于2的浅埋隧道，以及土体黏聚力较小的土层条件中。后者虽然考虑到了滑动块周围土体对其影响，适用埋深比（H/D）大于2的深埋隧道中，但在某些黏聚力较大的土层，可能会出现计算后的上覆土压力过小，导致隧道支护压力不足，影响盾构施工安全。

2）为了增加仓内土体的流动性，伴随着泡沫剂、水泥浆液等的混入，仓内土体参数不断改变，因此很难通过公式直接计算仓内土压力[7-8]。目前关于土仓压力的研究中，一般近似将盾构机掌子面前的极限支护压力当做土仓压力。通过对盾构机掌子面进行力学分析，求出其极限支护压力，以此作为土仓压力设置的依据。但在盾构机实际工作过程中，土仓作用在掌子面上的压力并不等于极限支护压力。这是由于在盾构机开挖过程中，为了尽量减少地表沉降、加快施工进度，多数情况下盾构机处于超挖状态。即土仓压力大于极限支护压力，此时盾构机面板会对前方土体造成一定的挤压。其力学计算公式如下：

式中，P预压力为盾构机面板后千斤顶所提供压力，一般为10～20 kPa。

4.2 上覆土压力计算

传统的上覆土压力一般采用朗肯土或库伦土压力进行计算，不考虑土体的黏聚力和抗剪强度，适用于开挖区域位于软土地层和位移较小的情况[9-10]。相对于传统的土压力计算公式，太沙基松动土理论考虑了土体在开挖过程中隧道尺寸、埋深、土体黏聚力、内摩擦角等对支护压力的影响。松动土体在自重作用下与周围土体产生相对位移，在抗剪力的作用下，一部分压力传递至周围土体，形成拱效应，且随着开挖深度的增加，拱效应越来越明显。但当土层黏聚力较大时，可能会出现覆土压力过小甚至为负值的情况，导致盾构隧道支护压力与实际施工状况有较大差异。因此，在计算中，需要结合土层信息与实际情况具体分析判断。此时，其计算公式如下。

1）太沙基松动土压力计算公式，为

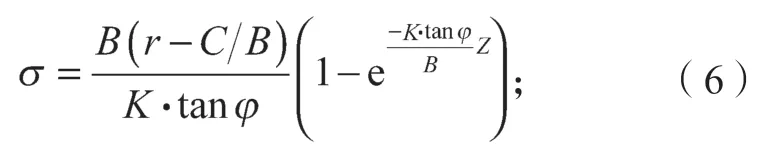
式中：B为土条宽度，且B=r+r·tan(45°-φ/2)；

r为隧道半径；

Z为土条埋深。

2）朗肯土压力计算公式，为

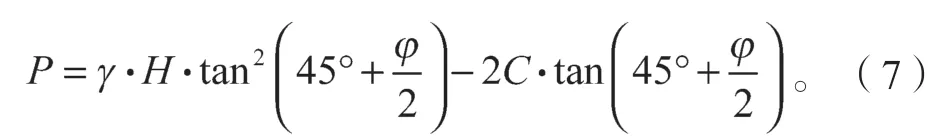
式中：γ为土体重度；

H为隧道埋深。

4.3 不平衡出土量计算

土压平衡盾构机在正常挖掘过程中，将前方削切的土体通过螺旋机传送至后方土仓内，同时盾构机继续向前推进。在理想状况下，盾构机削切土的体积应该等于排出土的体积，这时的盾构机才处于土压平衡状态。但实际上这种状态很难实现，盾构机通常都处于超挖或欠挖状态，即盾构机前方削切土的体积大于或小于螺旋机排出土的体积。大多数情况下，为了保证开挖面稳定，盾构机掘进过程中处于超挖状态，挤压前方土体以减少地面沉降[2-4]。其公式为：

式（8）（9）中：dV推进为单位时间削切土的体积；

dV排出为单位时间排出土的体积；

dV挤压为单位时间面板接触力对土的压缩体积；

D为盾构机最大开挖直径；

v为盾构机掘进速度；

dT为单位时间的螺旋机排土量。

将式（8）除以隧道截面积，即可得到盾构机掘进时土的不平衡掘进量dL：

式中S为隧道截面积。

4.4 改进后的土仓压力公式

经计算，当dL=0时，盾构处于土压平衡状态；当dL>0时，盾构处于超挖状态，刀盘面板对前方土体有一定的挤压力；当dL<0时，盾构处于欠挖状态，此时掌子面上土体朝隧道内移动，存在地表可能出现沉降的风险。通过不平衡掘进量与土层的水平基床系数，可求出土体在面板接触挤压下的挤压力P挤压：

式中Kv为土层的水平基床系数。

最终得到如下盾构机在推进过程中土仓压力的力学公式：

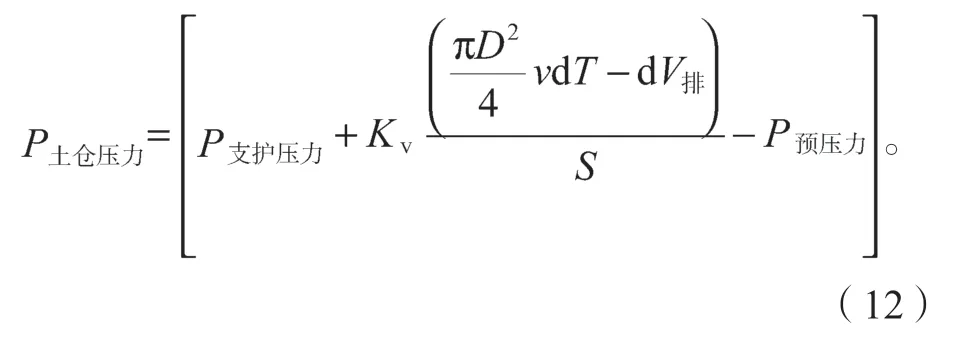
式（12）所示的土仓压力计算公式与传统的土仓压力计算公式相比，同时考虑了盾构机推进速度、排土量、隧道埋深比等因素对土仓压力的影响，更加贴合实际。计算的土仓压力值会适当大于极限支护压力值，使得盾构前方土体受到挤压，地表轻微隆起，随着盾构机的掘进通过，在管片和注浆的作用下隆起会逐渐下降，最终恢复稳定，地表沉降明显降低[11]。

5 有限元分析

5.1 模型概况

1）模型区域。为提高模型计算效率、简化计算过程，取盾构区间中连续的40环建模。整体沿模型Y方向为50 m，X方向为60 m，Z方向为40 m，深埋隧道圆心距地表约22 m，浅埋隧道圆心距地表约8 m。模型四周及底部采用边界约束，不考虑地下水对隧道开挖的影响。构建的整体网格模型如图2所示。

图2 工程整体网格模型Fig.2 Overall network model

2）模型参数。采用摩尔-库伦本构模型，对地层土体进行描述，利用Midas有限元分析软件对盾构施工开挖过程进行模拟。模型中包括的实体有盾构机外壳、管片，以及管片与盾构机外壳接触面设置的注浆层。管片前段设置千斤顶推力，法向位置设置注浆压力。设置的隧道网格模型如图3所示。

图3 隧道整体网格模型Fig.3 Overall tunnel model

3）计算工况。结合盾构机实际施工状况，每次开挖两环随即进行注浆和管片支护。在开挖面前方设置不同的土仓压力，研究在盾构区间内，改进后土仓压力计算公式的正确性与适用性，以及掘进速度对地表沉降的影响。

5.2 模拟结果分析

5.2.1 深埋隧道土仓压力对地表沉降量的影响

模拟所得深埋隧道土仓压力对地表沉降量的影响结果如图4和5所示。

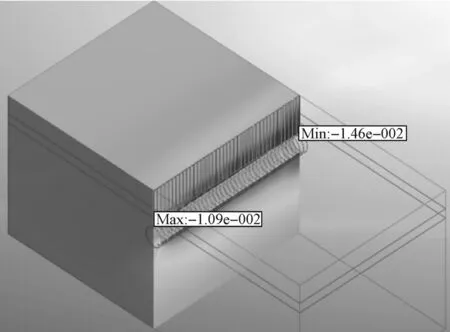
图4 深埋隧道纵向线上图Fig.4 Longitudinal line view of a deep-buried tunnel

经计算，当深埋隧道（隧道埋深比H/D>2）上覆土压力为太沙基松动土压力时，土仓压力为90 kPa。初始盾构阶段地表沉降量为10.15 mm，随着盾构机掘进的不断深入，地表沉降缓慢增加，最终的最大沉降量为12.24 mm，位于模型最后一环，如图5所示。上覆土采用朗肯土压力后，土仓压力计算值为120 kPa，地表初始沉降量为13.38 mm。虽然在隧道中间段地表沉降量有所减少，但随后依然会缓慢增加，最终总体沉降量大于上覆土为太沙基松动土压力时的。但当土仓压力为100 kPa时，总体地表沉降趋势更加平稳，且最终沉降值更小，如图5所示。因此，土仓压力取值为90～100 kPa较为合理。

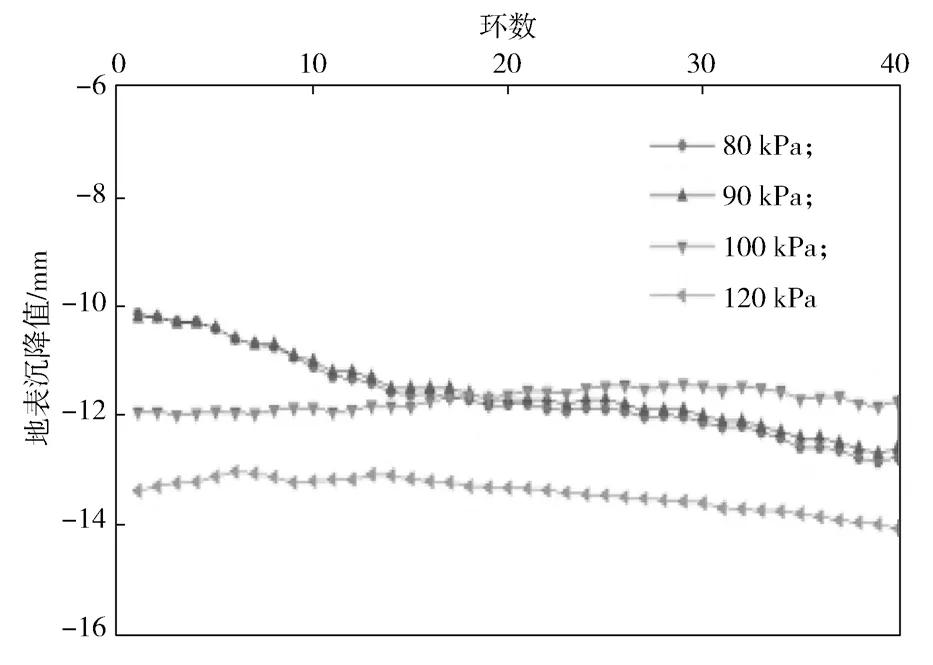
图5 深埋隧道地表沉降值变化曲线Fig.5 Surface settlement value of a deep-buried tunnel

5.2.2 浅埋隧道土仓压力对地表沉降量的影响

模拟所得浅埋隧道土仓压力对地表沉降量的影响结果如图6和7所示。

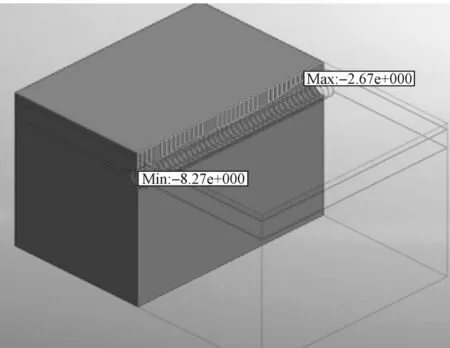
图6 浅埋隧道纵向线上图Fig.6 Longitudinal line view of a shallow-buried tunnel

当隧道埋深为8 m时，上覆土压力计算依然分别采用太沙基松动土理论和朗肯土压力理论进行计算。计算后的土仓压力分别为10, 30 kPa。初始阶段的地表沉降量分别为-8.27, -8.91 mm，但随着盾构机的掘进，沉降量逐步减少，最终的沉降量为-4.95,-4.17 mm，如图7所示。浅埋隧道整体沉降与深埋隧道的相比明显较小，整体变化趋势也完全不同，初始阶段的沉降值稍大，但随后的沉降值明显较少。当土仓压力增加为50 kPa时，地表沉降值相比计算值并未出现明显变化，如图7所示。

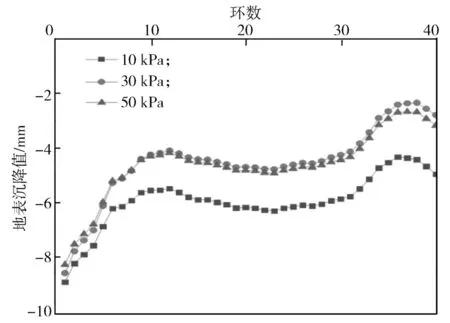
图7 浅埋隧道地表沉降值变化曲线Fig.7 Surface settlement value of a shallow-buried tunnel

5.2.3 掘进速度对地表沉降量的影响

由式（12）可知，盾构机掘进速度会直接影响挤压力的大小。改变掘进速度，分别设为30, 50, 70 mm/min，探讨掘进速度对地表沉降量的影响，所得隧道纵剖面Y轴方向的位移云图见图8，不同掘进速度下的地表沉降值见图9。

图8 隧道纵剖面Y轴方向的位移云图Fig.8 Displacement cloud diagram of the tunnel longitudinal section in Y-axis direction

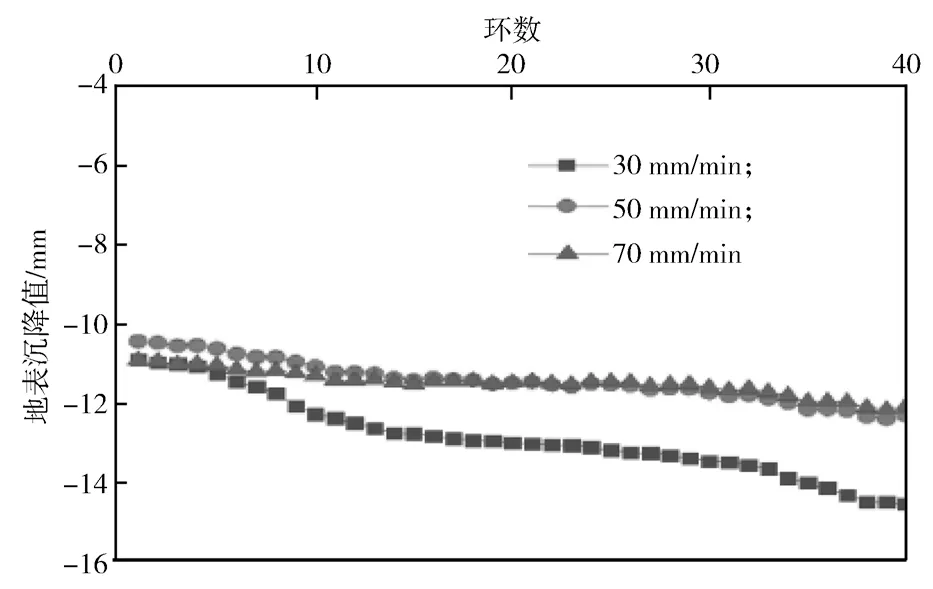
图9 不同掘进速度下的地表沉降值Fig.9 Surface settlement value at different excavation speeds

如图9所示，当掘进速度为50 mm/min时，掌子面前方土体在土仓压力的挤压下，朝开挖方向移动；当掘进速度为30 mm/min时，由于出土量增加，土仓所提供的挤压力不足，掌子面前方土体朝隧道内侧移动。通过对图9所示地表沉降值的分析，得知当掘进速度为50～70 mm/min时，地表沉降值明显较速度为30 mm/min时小。

6 结语

本文首先介绍了国内外关于土仓压力的研究现况，指出了传统土仓压力计算公式存在的不足之处。然后，通过对盾构机掌子面进行力学分析，基于Janssen&Koenen滑动土三维楔形模型，推导出了改进后的土仓压力计算公式。最后，结合实际工程案例，利用有限元分析软件，验证了改进后土仓压力理论计算公式的正确性，且针对浅埋和深埋两种情况下的隧道挖掘进行了讨论与分析，结果表明：

1）浅埋时，由于隧道整体沉降量较小，隧道所产生的自拱效应较弱。上覆土压力的计算应采用朗肯土压力模型进行，计算所得的土仓压力较大。该压力可为掌子面提供有效的支护压力，该土仓压力下，地表沉降量相对较小。

2）当隧道为深埋隧道时，隧道整体的沉降量明显增加，土体抗剪能力得到较大发挥，隧道自拱效应明显。因此，应采用太沙基松动土压力作为上覆土压力计算的依据，这样能够有效减少在开挖过程中掌子面对前方土体的扰动，降低了地表沉降。

3）为了保持开挖面稳定，降低地表沉降，应控制土仓出土率，适当增加土仓压力，合理地控制掘进速度。