城市道路混合路由算法研究
谷志茹,荣 青,李 敏,黎朝晖,信志平
(湖南工业大学 轨道交通学院,湖南 株洲 412007)
1 研究综述
在新兴的车联网通信系统中,因车联网拓扑结构的高速变换且复杂难测,使得各网络节点信息分布不均匀,资源调配难以有效满足不同环境下的通信需求[1]。因此有研究者提出在交叉路口和双向快速4车道两类交通场景下,对按需距离矢量路由(Ad hoc on demand distance vector routing,AODV)和目的节点序列矢量路由(destination sequenced distance vector routing,DSDV)进行性能比较[2],结果表明不同路由算法对不同场景的表现性和适应性均不同。故本研究选取城市道路上复杂多变的交通路口作为研究场景,在此场景下,因路边单元实时与过往车辆进行信息交互,交通灯覆盖的通信区域内可能会出现车辆密度突变而导致的车联网系统信息冗余和数据丢失等问题。本文拟对车车通信时所涉及的路由算法进行综合研究。
已有研究中,所涉及的基于地理位置的路由算法大多采用贪婪周边无状态路由(greedy perimeter stateless routing,GPSR)[3]的转发思想,且总是选择离目的地最近的节点转发,以减少路径消耗,但对节点位置信息要求极高,且易陷入路由空洞。文献[4]对其进行了优化,在选择下一跳节点时,选传递范围内最可靠的节点转发,在高速、网络密集的环境中,极大地减少了时延和节点跳数,提高了可靠率。但在低速、网络稀疏的环境中,其性能不佳。文献[5]利用人工蜂群算法寻找最小转发路径,避免陷入路由空洞。但若两节点相距较远,路径规划会增加计算复杂度和时延性能,这是因为虽避免了路由空洞,但节点跳数增多。文献[6]在选择下一跳节点时,综合考察了两节点间的节点接近率和下一跳节点前向转发区域密度,以此作为评价指标,择优选择下一跳节点,避免多跳状态信息造成的路由开销。文献[7]提出了路径感知GPSR策略,即在节点陷入路由空洞时复制数据包,并同时使用左手和右手转发规则,以绕过路由空洞。文献[8]针对交叉路口环境下的数据转发情形,在选择下一跳节点时,兼顾链路稳定性和距离衰减性等因素,提前预测路口节点,使数据包能够利用路口协调节点来投递数据,避免了路由环路问题。
基于拓扑的路由算法采用按需距离矢量路由AODV[9]的转发思想,节点通过广播路由请求包和回复路由应答分组,建立路由通路。但网络过于密集或稀疏都会影响通路的建立。针对这一问题,文献[10-11]根据接收节点所处环境信息动态配置节点等待时延和转发概率,再按优先级先后转发,避免了局部网络风暴和传输延迟等问题。
综上可知,无论是基于地理位置还是基于拓扑的路由算法,在红绿灯路口下的适应性和表现性都有所不足,如:
1)节点密度骤增时,贪婪转发算法因周期性地进行邻居列表访问,信息更新过于频繁,因而导致计算复杂,工作量增大;
2)节点密度骤减时,距离矢量转发算法在高速移动的节点间无法建立稳定的路由通路,数据投递准确率低且存在极大的传输时延。
针对以上算法在红绿灯路口下实施时存在的弊端,提出一种自适应限制性混合路由算法(adaptive restrictive hybrid routing protocols,ARHP),对其进行优化:
1)对各节点数据投递时的通信区域设置限制条件,并在受限区域内对节点密度、运动方向和速度进行考察,通过权重分析择优选取下一跳节点。
2)针对不同的网络环境设置不同的转发模式,通过对当前网络状态进行实时评估,完成转发模式间的切换。
2 ARHP路由算法的构成
2.1 受限贪婪转发
基于地理位置的路由GPSR选择下一跳节点时,仅通过判断各节点间的欧氏距离,就盲目地投递数据包,极易陷入路由空洞。针对这一问题,提出从多方面考察链路质量,对其进行综合评价,以此择优选取下一跳节点,其中可考察的因素为通信范围内的有效邻居节点数和两通信节点间的链路生存时间。
2.1.1 有效邻居节点数
在选择下一跳节点时,需考虑通信范围内的邻居节点数量,可对节点的通信范围进行限制。邻居节点通信区域内的受限节点数量如图1所示。
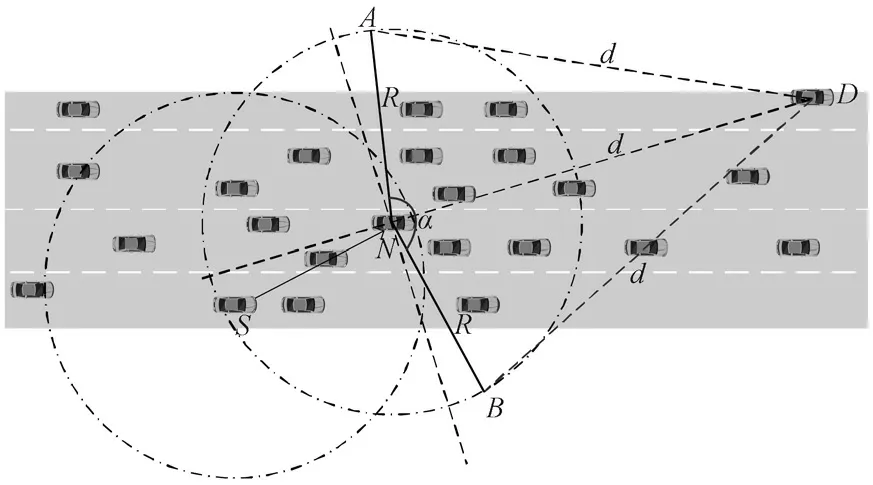
图1 邻居节点通信区域内的受限节点数量Fig.1 Number of restricted nodes in communication region of neighbor nodes
由图1可知,将所考察的下一跳节点与目的节点相连接,以考察的下一跳节点为原点,最大通信距离R为半径,画一个圆,在圆上所有与目的节点间距离短于原点到目的节点间距离的节点均纳入原点的邻居节点考察范围。即在考察范围内的节点均需位于平面角度为α的扇形区域内,且满足

式中:R为节点的最大通信半径;dND为邻居节点N(xN,yN)到目的节点D(xD,yD)的距离,其值可由式(2)得到。
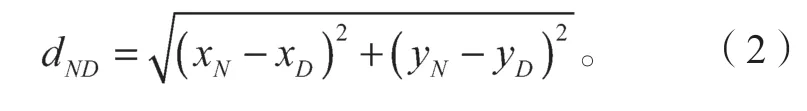
若已知邻居节点通信范围内的任意节点i的坐标为i(xi,yi),可求出节点i到目的节点D的距离:
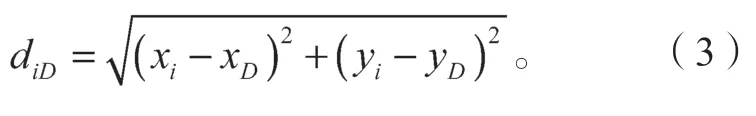
结合式(2)和式(3),可求得任意节点i对应的距离函数fi。
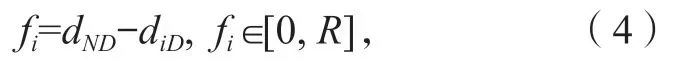
式中fi的有效取值范围为[0,R],若任意节点i的距离函数不在此区间,则视该节点为无效节点。
设随节点有效性变化的因变量为K,当任意节点i同时满足公式(1)和(4)时,K>0,有效邻居节点数量为n+1;反之,K≤0,节点不计数。故有效节点密度(effect node density,DEN) 如下:

式中:n为通信范围内有效邻居节点的数量,初值为0;Ntotal为通信范围内所有节点数量。
2.1.2 链路生存时间
假若源节点S和邻居节点N在现阶段相互保持着链路通信,经过一段时间后,两节点的相对位置发生偏移,链路断裂。这段时间即为两节点的链路生存时间,可由源节点S和邻居节点N的位置、速度联立求解获得。
已知S(xS,yS)为源节点,N(xN,yN)为邻居节点;根据坐标信息可求得节点S、N间的平面夹角θ和欧氏距离dSN:
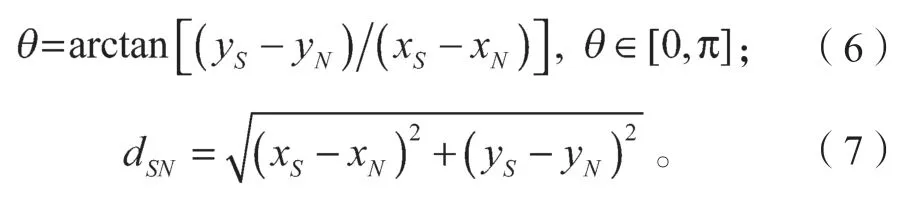
当两节点同向移动时,将式(6)(7)代入式(8)中,则可求出节点S、N间的最大链路生存时间TLink。
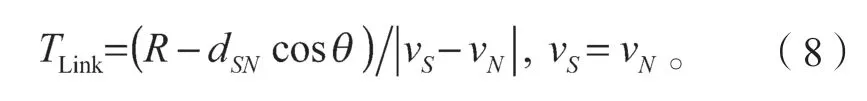
式中:vS为源节点S的移动速度;vN为邻居节点N的移动速度,vS=vN表示两节点同向;当间距dSN一定时,角度越大,链路生存时间TLink越长。
同理,当两节点反向移动时,根据两节点的相对位置,即可求出节点S、N间的TLink。
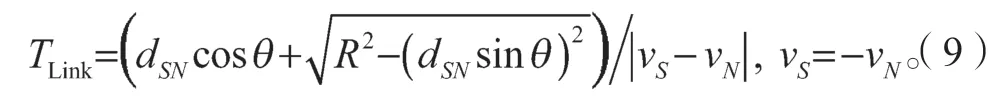
式中:vS=-vN表示两节点反向;当间距dSN一定时,角度越大,链路生存时间TLink越短。
当两节点反向移动时,若要计算链路生存时间,需提前考察式(10)是否成立。
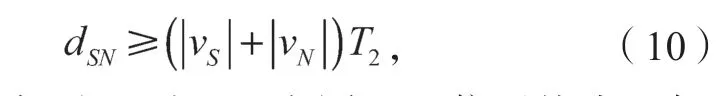
式中,T2为数据处理时延,在同一通信系统中,任意两节点间的数据处理时延近似相同。
在数据传输期间,源节点S和邻居节点N的相对位置发生变化,其变化示意图如图2所示。

图2 经T2后,两节点相对位置变化情况示意图Fig.2 Changes of the relative positions of two nodes after T2
在图2a中,经过时间T2后,源节点与目的节点间距离d1大于邻居节点与目的节点间距离d2,即d1>d2时,可将邻居节点N纳入可选节点,并将其与源节点S间的链路维持时间TLink×1。
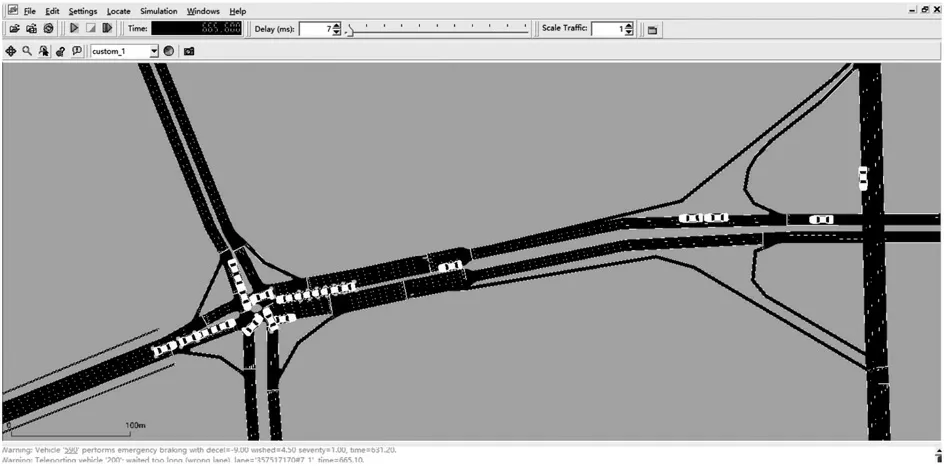
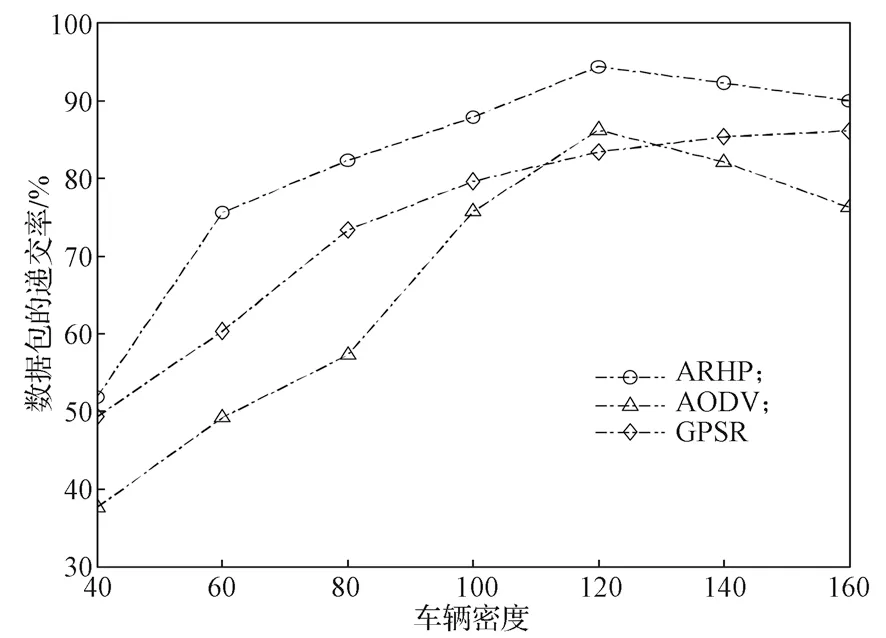
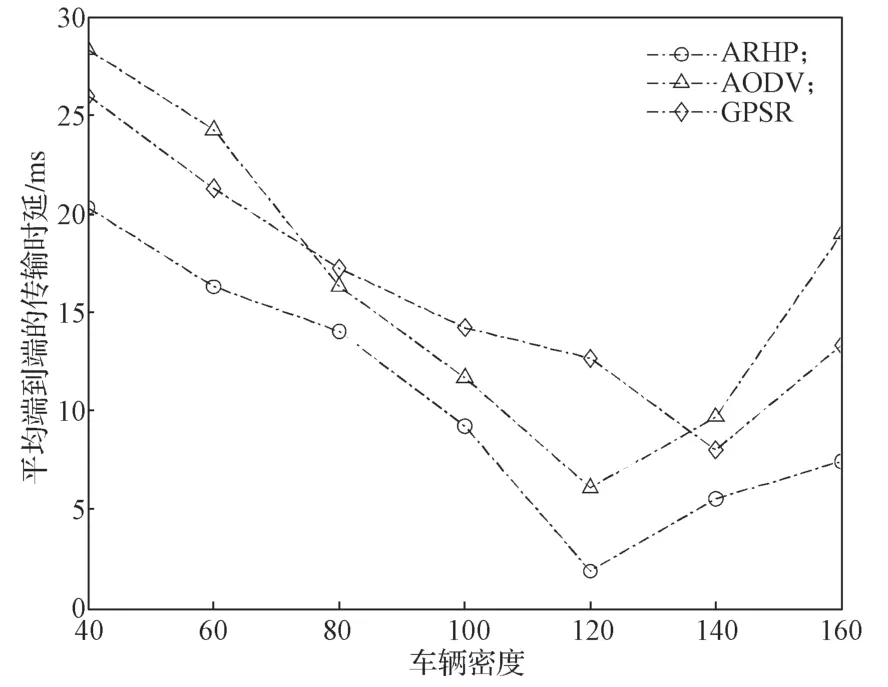
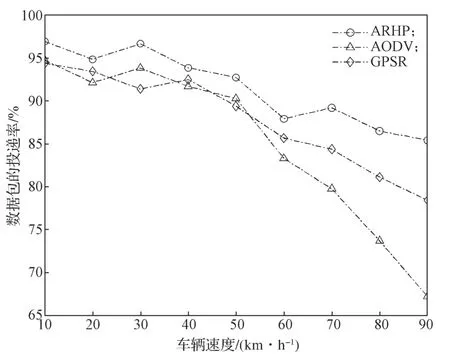
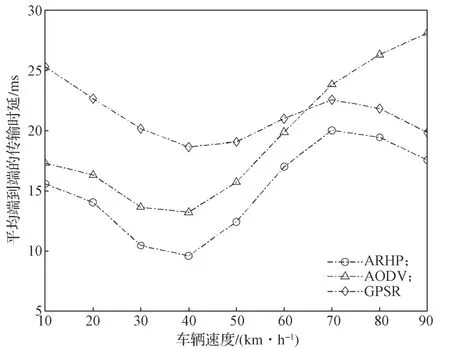
图2b中,经过时间T2后,d1 设随数据交互后节点间位置变化而变化的考察变量为Q,经过时间T2后,若d1>d2,则Q>0,链路维持时间为TLink×1;反之,若d1 综合考虑链路生存时间和有效邻居节点密度,对它们进行层次权重决策分析,并建立链路质量的相关权重函数Lquality。 式 中:w1、w2为权重值,且w1+w2=1,0 通过以上的优化改进,数据包可在限制性条件下高效投递。但在网络密集处,受限贪婪转发因缺乏一个已建立的稳定路由,导致每个节点每一次数据投递都要对邻居节点集进行计算,计算负载大。因此,提出距离矢量转发机制探知数据投递路径,按需建立稳定路由,针对交通拥堵、车辆密集的场景,提前做好线路规划。 由于距离矢量转发能高效传递数据信息的前提是建立稳定路由。故可对当前网络状态进行实时评估,以评估值作为两种转发模式间的切换依据。其中常用的评估指标有:节点位置偏移、邻居节点数量变化率。 2.2.1 节点位置偏移 分别设当前节点S和其任意邻居节点i在t-1时刻的位置坐标为、,目的节点的位置坐标为D(xD,yD),可得出节点S与目的节点D间的平面夹角,为 任意邻居节点i与目的节点D间的平面夹角可表示为 同时,可求出在t-1时刻,节点S和节点i的间隔距离,为 已知当前节点S的移动速度为vS,可预测出该节点在下一时刻t相对于目的节点的偏移位置[12]: 同理,已知任意邻居节点i的移动速度vi,可预测出该节点在下一时刻t相对于目的节点的偏移位置,为。 由式(15)和式(16),再联立邻居节点的偏移位置it求解,可得出t时刻节点S和节点i的间隔距离,为 由式(14)(17),可以得出当前节点的所有邻居节点位置总偏移(node position migrate,NPM)量dNPM,为 已知当前节点的所有邻居节点中移动速度最快和最慢的节点的速度为vmax、vmin;在t-1时刻到t时刻间,它们对应的最大位移量分别为S1、S2, 分析式(18)~(20)可知,当节点位置总偏移量dNPM≥S1时,视为动态网络;而当dNPM≤S2时,则视为通信区域内的节点处于相对静态状态。 2.2.2 节点数量变化率 节点数量变化率为当前节点在t-1时刻的邻居节点数Nt-1和t时刻的邻居节点数Nt差值的绝对值与Nt之比,即节点数量变化(change number,CN)率ηCN为 其中,Nt>0。当ηCN趋于0时,可认为通信范围内节点数量不变,网络连通性良好。 综合考察节点位置偏移和邻居节点数量变化率,对它们进行层次分析以判断当前网络状态(network status,NS),用VNS表示,为 式(22)中,ρ1、ρ2均为权重值,且ρ1+ρ2=1,0<ρ1<1, 0<ρ2<1。当VNS≥max{dNPM,ηCN}时,状态标志位Flag=1,采用受限贪婪转发。当VNS趋于0时,网络状态标志位Flag≠1,切换至受限距离矢量转发模式。 在交叉路口的网络通信环境下,设计车与车之间的网络布局和数据交互方式,其中所涉及的ARHP路由算法的具体实现过程如下。 step 1对当前节点通信范围内所有邻居节点进行链路质量权重值计算,根据所求Lquality值判断该节点是否参与竞争转发; step 2若Lquality≤0,则不参与竞争。当所有邻居节点的Lquality值皆小于0时,当前节点暂存数据包,并不断访问邻居列表直至耗尽数据包的生存期; step 3若Lquality>0,该节点参与竞争转发,将Lquality反馈回当前节点,对其所处网络状态VNS进行实时评估。 step 4当网络状态标志位Flag=1,采用受限贪婪转发进行数据投递。即当前节点将各邻居节点反馈回的Lquality值从高到低依次排列,择优选取权重值最大的节点进行投递; step 5当网络状态标志位Flag≠1时,转发模式切换为距离矢量转发;即节点仅向平面角度为α的区域内的邻居节点不断地广播路由请求包,以建立路由通路,使此后的数据可直接在此通路投递,无需进行额外计算。 在整个数据传输过程中,需时刻对当前网络状态VNS进行判断,一旦达切换阀值即切换转发模式。也需实时判断当前节点是否为目的节点,若为目的节点,说明数据已传输成功,退出当前通信网络;反之,重复以上传输过程,直至数据投递完成。 实验采用开源网络仿真平台NS-3仿真网络算法,以交通模拟器SUMO(simulation of urban mobility)模拟车辆在遇到红灯或绿灯时的运动轨迹。对ARHP进行不同环境下的实验仿真,并分析对比ARHP、AODV和GPSR多种路由协议在数据包的递交率和端到端时延上的性能表现。 在OpenStreetMap官网上导出湖南省株洲市天元区的地图。利用SUMO的工具插件对其进行处理,获得道路环境信息,选取模拟区域2 000 m×1 000 m,10个红绿灯路口、15条双向两车道的道路交通模型。车辆的初始位置是随机分布的,车辆在道路上的运动受车辆沿道路跟随模型(Kraus模型)的限制。且每辆车都配备了全向天线和GPS定位器,可获取车身的位置、行驶方向、运动速率等信息,并实时与其他车辆节点共享。任意选定其中一个红绿灯十字路口,其仿真道路场景如图3所示。 图3 仿真道路场景图Fig.3 Road simulation scene 图3中,车辆随机进入等待红绿灯行列,进入的车辆数取值范围为[40,160]。假设车辆在绿灯场景下均匀速行驶,其取值范围为[10,90] km/h,仿真场景参数见表1。 表1 仿真场景参数Table 1 Simulation scene parameters 设计两组实验,一组实验设置固定车速为v=60 km/h,令节点密度为[40, 160],步长为20;另一组实验设置固定节点密度n=120,车速变化范围为[10,90] km/h,步长为10。进行多次实验取其均值,分析各算法在不同节点密度和车辆速度下的性能表现。仿真时所采用的性能指标定义如下。 1)包的递交率。指目的节点接收的包总数Nreceive与源节点发送的包总数Nsend的比值,它反映了网络数据传输的成功率(packet delivery rate,PDR),符号为rPDR,即。 2)平均端到端时延(average end-to-end delay,AEED)。指将所有数据包接收和发送之间的时间差ti求和并取均值,其反映了网络数据传输效率,符号为AEED,即。 为了评估节点密度对系统通信性能的影响,实验一对ARHP、AODV和GPSR在数据包的递交率、平均端到端的时延等方面的性能表现进行仿真分析,取其均值构成关联曲线图,实验结果见图4和5。 图4 不同节点密度下的数据包递交率变化曲线Fig.4 Change curve of packet delivery rate under different node densities 由图4所示不同节点密度下的数据包递交率的对比结果可知,随着节点密度的增大,路由环境趋于稳定,GPSR和AODV的递交率持续稳步增长,在节点密度从n=80到n=120间时,AODV因所需的稳定网络结构完全搭建好,递交率快速增长了29%;而后因出现局部广播风暴,递交率有所下降。ARHP在节点密度小时,无法建立牢固的路由通路,故采用受限贪婪转发在扇形区域α内做最优数据投递路径选择;随着节点密度增大到n=120时,采用有限贪婪转发和距离向量混合转发模式,数据包递交率达最优值;然后完全采用受限距离向量转发模式,若节点密度持续增大,数据包的投递率因受环境因素的影响而有所降低。但ARHP投递率仍平均比AODV和GPSR分别高16%, 8%以上,体现了ARHP选择下一跳节点时,根据受限条件和所处通信环境,采用了最有利的转发模式。 由图5所示不同车辆密度下端到端的传输时延大小可知,节点为n=40时,网络连通性较低,易陷入路由空洞和造成数据丢失,端到端的时延值均较高。节点数在80到120间时,ARHP的端到端时延大幅度下降,降到1.8 ms,因节点密度增加,路由通路已建好,下一跳节点选择时无需实时进行参数计算便可维持高效的距离向量转发。当n>120后,网络出现局部密集,路由通路的建立和节点间数据交互所需的时延增大,ARHP的传输性能下降,但结果显示ARHP较AODV、GPSR数据传递造成的端到端时延仍低6%以上。 图5 不同节点密度下平均端到端传输时延曲线Fig.5 Transmission delay curve of average end-to-end delay under different node densities 为评估不同车速对通信系统性能的影响,实验二对ARHP、AODV和GPSR在不同车速下的各方面性能表现进行了数据分析,实验结果见图6和7。 图6 不同车辆速度下数据包递交率变化曲线Fig.6 Variation curve of packet delivery rate under different vehicle speeds 图6为不同车速下的数据包投递率对比结果。由图可知,车速较低时,网络连通性好,三者的投递率均有较好的性能表现。随着车速增大,投递率均逐渐降低,当车速大于v=60 km/h时,网络拓扑结构高速变换,许多路由通路断裂,数据包大量丢失或传输错误,GPSR和AODV的投递率分别急速下降了7.3%和16%。ARHP因进行了高效的数据投递,且根据环境自适应的调整信标间隔周期,快速地适应车速变换带来的邻居列表更新频率,高效组网构建路由通路,极大地减缓了投递率的下降速度,性能表现优于AODV和GPSR。 图7为3种路由协议在不同车辆速度下平均端到端的时延。由图可知,车速较低时,路由通路稳定,GPSR因需对邻居节点进行周期性参数计算,端到端的时延偏高。随着车速增大,链路连通性降低,AODV无法建立稳固的路由通路,需反复进行路由访问,因而增加了节点跳数和传输时延;GPSR和ARHP因其路由传输特点,受到速度变化的影响相对较小,故两者的传输时延均低于AODV。 图7 不同车辆速度下平均端传输到端时延变化曲线Fig.7 Variation curve of average end-to-end transmission delay under different vehicle speeds 本文提出一种基于贪婪转发和距离向量转发的快速组网混合路由算法ARHP,解决了城市道路红绿灯路口场景下,车辆密度突变给通信系统带来的信息冗余和数据丢失等问题。ARHP算法结合了贪婪转发对邻域节点选择的高效性和距离矢量转发对降低计算复杂量的优化性。在贪婪转发中,对链路质量和端到端时延值综合考察,对邻域节点进行最优选择,网络密集时切换至距离向量转发模式,减少不必要的计算量,这样可以有效缓解网络负载过重问题,节约数据传输开销。对ARHP、AODV、GPSR 3种路由算法进行数据分析,大量的实验仿真结果表明,随着节点密度和移动速度的增大,ARHP算法在多方面的性能均优于AODV、GPSR路由算法。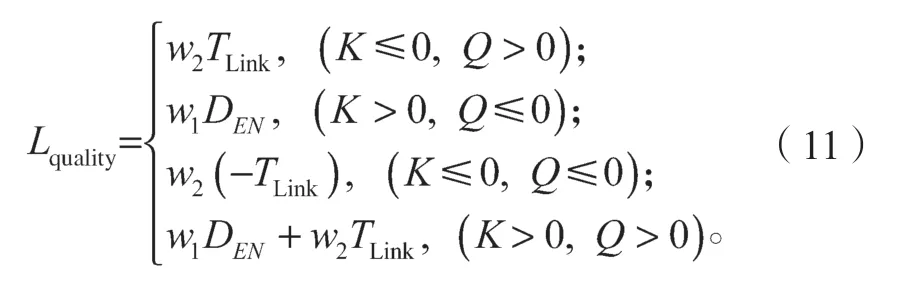
2.2 网络状态评估
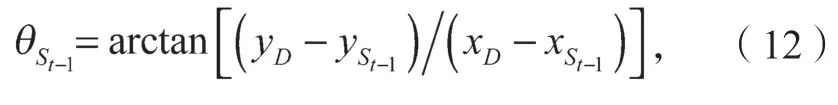


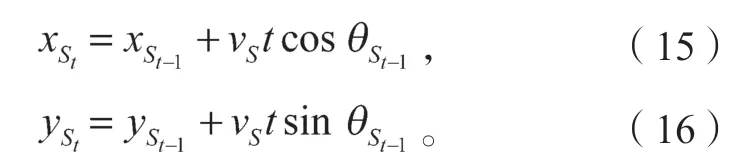
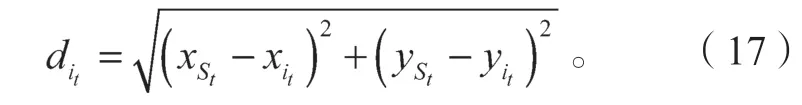
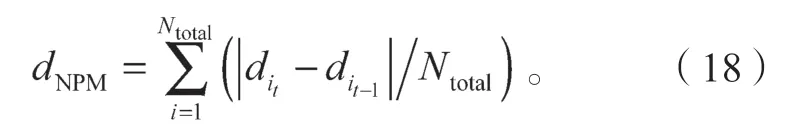

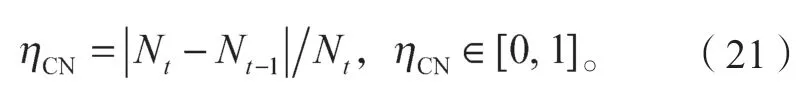

2.3 具体实现过程
3 仿真分析
3.1 场景设置

3.2 结果分析
4 结语

