基于WT时频分析和最大类间阈值法图像分割的机械故障诊断

曾 成，孙 晓，李文杰，李西宸

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

现代机械装备运行精度要求较高、使用寿命要求较长，机械故障诊断技术[1]已经成为设备健康维护的重要手段。现代故障诊断技术多采用多学科、多专业交叉融合的方法进行预测、监测以及诊断，以实现设备的全寿命周期监控，该技术对设备软故障和硬故障的判定和预测及设备的运行和维护，具有十分重大的意义[2]。

机械故障监测与诊断一般包括3个环节，首先是对设备运行状态进行监测，通过各类传感器获取机械关键部位的运行数据，得到机械振动信号；然后通过传感器采集到的各类数据，结合数学和信号处理等学科知识进行相应的信号预处理，如采用加速度传感器，通过数学积分可以得到机械振动数据，从而得到有效的信号特征和故障特征；最后，将提取的故障信号特征与特征库里的数据进行匹配识别，从而实现对设备运行状态的监测及故障情况的诊断。

张立智等[3]提出了基于经验模态分解（empirical mode decomposition，EMD）和奇异值分解（singular value decomposition，SVD）的深度卷积神经网络（convolutional neural networks，CNN）机械故障诊断方法。该方法通过构建时频域的状态矩阵，提取其奇异值，然后导入卷积神经网络中，该方法较常规卷积神经网络故障诊断具有更高的准确率。黄鑫[2]提出了一种基于卷积神经网络与离散小波变换的行星齿轮箱故障诊断方法，可对信号进行频域上的分解，并可对不同频带的信号进行分析。鄢仁武等[4]提出利用AlexNet卷积神经网络模型，以压缩的时频图作为特征图进行故障诊断；黄驰城[5]提出先对轴承故障进行来源分析、理论校对，再结合深度学习进行故障诊断；向玲等[6]对旋转机械的非平稳信号进行了研究，采用不同的时频转换方法得出其时频二维图，有效地从时频域对故障信号进行了表征。

上述方法大多是利用CNN直接对故障信号进行特征提取，这种方法需要大量的数据进行训练，而改善网络模型是一个较为复杂的调参过程，模型和数据处理时间较长。针对上述方法中存在的问题，本文提出一种基于小波变换的时频信号处理技术，通过对信号进行可视化处理，得到时频域的热力图形式故障信号特征，再结合图形学，对时频图进行形态学滤波、灰度转换、二值化等处理，得到能有效表征各频率成分的信号图[7]。课题组拟将该方法应用于美国凯斯西储大学的电机轴承数据库，以期得到较好的故障诊断效果。

2 基于小波变换的时频热力图

机械故障在时域上有累积性和突发性，如齿轮箱里各齿轮存在的齿裂、齿根磨损，电机轴承内圈、外圈、滚动体的点蚀、裂痕，这些看似正常的损伤，都会在设备的运转中日益变大，最终会导致显性故障[8]。通过在设备相应位置安装加速度传感器便可以采集到机械设备的振动信号，而这些振动信号可以反馈设备故障程度[9]。

传统的时域信号虽然能有效反映机械振动情况，但是前期故障信号并不会以一个较大的峰值出现，而是以一些不同的频率成分存在于振动信号之中，并存在渐变过程。所以将设备的时域信号转换到频域，以热力图的形式将其信号能量强度反应在时频域上，能更方便表征故障信息。

2.1 连续小波变换

利用小波变换（wavelet transform）的特性，可以有效地将一个时间信号通过合理的尺度转换到时间频率域，以便更好地观察信号自身的某些局部特征。同时观察信号的时间和频率信息，由于小波变换[10]大冗余度的特点可以利用时间和频率域部分信息完整地表示信号的长期特征。

小波变换实际就是利用一系列相互关联的函数来表示信号的主要特征，这一系列函数就是小波函数系。设函数为

式中：φa,b为分析小波或者连续小波；

φ为母小波或者基本小波；

a为改变小波形状的伸缩因子；

b为小波位移的平移因子。

对于某一函数f(t)∈L2(R)的连续小波可以通过式（2）变换为Wf(a,b)：

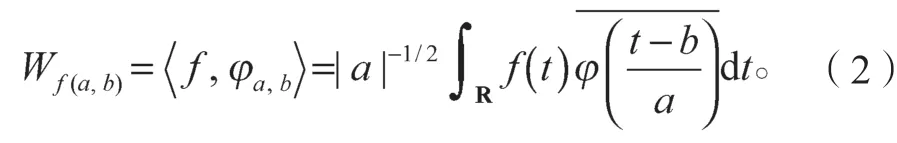
符号为两者的内积，所得结果为尺度为a、位置偏移为b的小波函数的系数，表征该小波函数与原信号的相似度。其中，a和b都属于连续变量，因此称之为连续小波变换。

2.2 振动信号的WT时频分析

信号的时频分析可理解为信号在时域和频域上的一种不同分布情况，该分布为将一维时间信号映射到由时间轴和频率轴组成的二维时频平面上的能量分布[11]。随着小波系数a、b的变化，各个基函数将拥有不同的时频域集中中心，信号的小波变换结果反映不同时刻不同频率成分能量大小[12-13]。

步骤1设伸缩因子即变换尺度为a，采样频率为fc，小波的中心频率为fs，则a所对应的实际频率fa为

步骤2由式（3）可得，转换的频率序列应为等差序列，其尺度序列选取c/ltotalscale，c/(ltotalscale-1)，…，c/2，c形式。

其中，ltotalscale为对信号进行小波变换时所用的尺度序列长度；c为常数。

步骤3由步骤1、2可得，尺度c/ltotalscale所对应的实际频率应为fs/2，于是得

故可以得出尺度序列t。

步骤4在确定小波基的尺度序列后，便可以根据式（2）连续小波变换的原理求出对应的小波系数Wf(a,b)，然后由所得尺度序列转换为实际频率序列f，最后结合时间序列t，可以绘制出基于小波变换的时频二维图，获取信号的特征信息。

图1所示为振动信号时频转换示意图。

比如要换一个人，这个员工会认为：组织想换我，我要留一手，开始考虑个人利益。作为组织来说，因为这个业务还得做，企业还要活下去，没有更好的人，还得用他。这样，员工和组织之间开始博弈，相互提防，进入一种负循环。

图1 振动信号时频转换示意图Fig.1 Vibration signal time-frequency conversion diagram

2.3 信号可视化处理

对经过WT（wavelet transform）时频分析后的振动信号进一步做信号可视化处理。即将时频域分布的信号以热力图的形式呈现出来，通过颜色深度的不同来表征时间域上不同频率成分的信号能量强度[14]。对频域上不同能量密集程度的区域可以初步划分为故障典型能量区和正常能量区域，以便为下一步的故障信号做预诊断处理。图2所示为图1a的时频热力转换图形式。

图2 时频热力转换图Fig.2 Time-frequency thermal conversion diagram

3 基于图像处理技术的特征强化

3.1 图像二值化

图像分割在图像处理、模式识别等技术领域的地位越来越重要，分割的效果将直接影响后续图像处理及科学分析的效果[15]。图像二值化一般分为全局阈值和Ostu阈值两种算法。Ostu阈值分割图像采取的运算方式是在灰度图基础上基于最小二乘法进行处理，所以在数值计算方面具有统计意义的最佳分割。全局阈值则采用单一阈值，将灰度图像中所有像素点的像素值与阈值进行比较，从像素的角度完成对图像像素的重新赋值和图像分割。

时频热力图具有完全一致性的背景颜色深度，所有具有偏差的像素值皆为表征所需要研究的频率成分，故课题组采用全局阈值法，对时频热力图进行图像分割，完成特征提取[16]，处理方式见式（5）：

式中：x、y为图像中各像素点位置；

T为所选用的阈值。

对图像中大于阈值T的像素点赋值为255，对像素值小于阈值T的像素点赋值为0。

3.2 不同二值化方法对比

3.2.1 均值阈值法

均值阈值法的本质是根据图像中每一个像素点位置处的像素值大小情况直接得出一个衡量平均水平的阈值，再利用该阈值对图像中的像素特征进行分割。先求出图像中各点像素，得出图像的像素均值，选取像素均值为阈值，遍历图像，对图像中像素值大于阈值的像素点赋值255，对图像中像素点小于阈值的像素点赋值0。从而实现对图像的二值化处理，对图像进行基于均值阈值的分割[17]。

3.2.2 自适应阈值法

采用基于Wall算法的自适应阈值进行分析处理[18]，该算法的本质内容是根据图像背景亮度情况动态地计算图像阈值。该算法先遍历图像各像素点，计算一个移动的平均值，如果其前后像素点的像素值低于这个移动平均值，则分别重新赋值为255或0，相当于是一个动态分块处理的均值阈值处理[19]。

假设Pn为图像中位于点n处的像素，就其中一行元素Pn-s、…、Pn-1、Pn，有如下推导。

假设fs(n)是点n处最后s个像素的总和，则

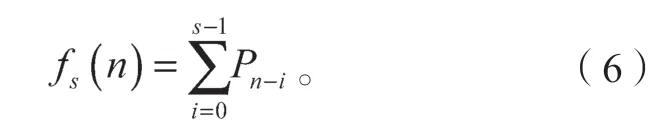
最后图像各点T(n)是255（白色）还是0（黑色），

则依赖于其前面s个像素的平均值t%的比较关系。

3.2.3 大津阈值法

大津阈值法又叫最大类间阈值法、最大类间方差法。它的基本思想，是用一个阈值将图像中的数据分为两类，选取两类中各像素点灰度的方差最大的阈值为最佳阈值。利用该阈值可将图像分为感兴趣的前景和不感兴趣的背景。方差作为灰度分布均匀性的度量方式之一，背景与前景之间的类间方差越大，说明两者差别越大[20]。故基于类间方差最大的分割就意味正确区分的可能性越大。

对于图像I(x,y)，记前景和背景的分割阈值为T，前景像素分布情况为α0像素点占全图比例，平均灰度值β0；背景分布情况为α1、β1。图像总的平均灰度值为β，类间方差为g。

假设有M×N的图像，其中灰度值小于阈值T的像素点个数记为N0，大于阈值T的像素点个数记为N1，则有：

将式（12）代入式（13），得到等价公式：

利用式（14）就可求得类间方差，采用遍历的方法使类间方差g最大的阈值T就是所求最佳阈值。

3.3 图像处理效果

将经WT时频分析后得出的时频热力图进行截取操作，得到如图3所示的时频特征提取图，对该时频特征图进行二值化处理后即可得出机械故障信号特征图。

图3 故障特征提取图Fig.3 Fault feature extraction map

如图4所示，采用大津阈值法，利用类间方差评估阈值的方法能较好地对图像进行分割，强化各频率成分特征。

图4 不同二值化方法强化效果对比Fig.4 Comparison of strengthening effects of different binarization methods

故课题组将采用该方法对各电机轴承振动信号时频热力图进行处理，以得到较好的机械故障诊断效果[20]。

4 实验验证

4.1 数据预处理

课题组选用美国凯斯西储大学电气工程实验室的滚动轴承故障模拟实验台提供的轴承故障数据库进行研究[3]。试验台由一个1 491.40 W的电动机进行驱动，中间放置一扭矩传感器进行实时监测。以驱动端轴承SKF6205作为研究对象，通过将加速度传感器放置于不同位置实现装置不同位置振动信号的提取。通过电火花加工单点损伤的方式，给轴承不同位置植入故障，从而实现机械故障信号的提取与分析[21]。图5为电机轴承实验装置图。

图5 电机轴承实验装置图Fig.5 Motor bearing experimental device

在驱动端，安装加速度传感器以48 kHz采样频率采集电机在1 797, 1 772, 1 750, 1 730 r/min转速下的正常振动信号和故障振动信号。针对内圈、外圈、滚动体3种不同轴承故障类型和0.177 8, 0.355 6,0.533 4 mm 3种不同程度的故障情况进行研究。通过信号可视化和图形学处理后，将故障信号特征与正常信号特征进行对比，可以有效提取出故障特征信息。表1为轴承具体故障情况和工作状况参数。

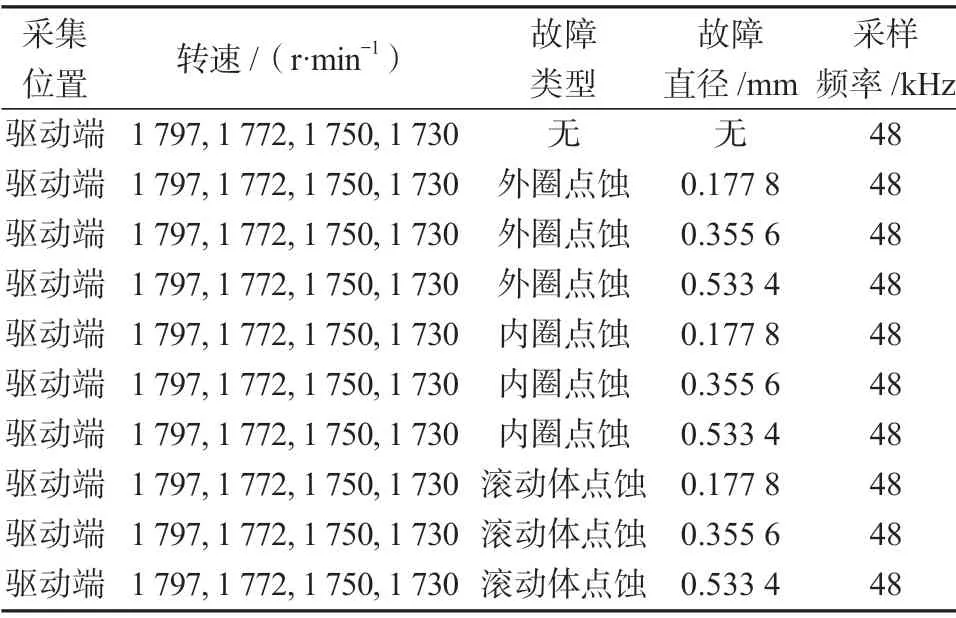
表1 轴承工况参数表Table 1 Bearing condition parameter table

4.2 时频热力图分析

图6为故障信号频率成分分布情况。

图6 故障信号频率成分分布图Fig.6 Fault signal frequency component distribution diagram

分别对采集到的正常信号和不同类型、不同程度的故障信号进行时域波形图的绘制。因为振动信号采样点较多，且信号幅值并无明显波动，故采用连续小波分析，利用其数据冗余度大的特点，将振动信号按一定的尺度变换转换到其时频域分布。并用热力图的形式通过颜色深度对其能量密度进行表征，图7为正常信号频率成分分布情况。

图7 正常信号频率成分分布图Fig.7 Distribution of normal signal frequency components

如图7所示，正常信号的时频热力图能较好地反映出长时间采集的机械振动信号中包含的和频率成分及其能量强度。但是对于某些能量强度较弱的频率成分还是有一定的识别难度。故需要进一步对其进行图形学处理，从像素的层面对其进行分割，以强化信号特征[22]。

4.3 基于二值化特征强化

将时频热力图中的时频成分进行截取与分析，以避免图片中的其他像素对图形学处理造成干扰。对图像进行二值化处理，强化各频率成分特征，将部分微弱故障信号的频率成分显现出来，所得信号特征图见图8和9。

图8 振动信号特征强化图Fig.8 Vibration signal feature enhancement map

图9 不同情况下故障信号特征图Fig.9 Fault signal characteristic diagrams under different conditions

对3种不同故障情况的机械振动信号进行基于连续小波变换的时频转换，对时频热力图进行图像二值化处理，所得故障信号特征如图10所示，对比图10和图8，可以看出，正常机械振动信号图像跟机械故障信号图像相比，具有明显的区别特征。

图10 不同情况下故障信号特征强化图Fig.10 Characteristic enhancement diagram of fault signal under different conditions

4.4 故障表征及诊断效果分析

将时频热力图中的时频成分进行截取与分析，以避免图片中的其他像素对图形学处理造成干扰，对图像进行二值化处理。

4.4.1 故障表征

对经过特征强化的时频分布图进行面积求解。考虑到保存所有频率成分信息，故采用8邻接的方式求取连通域，最大可能保全频率成分。将具有不同像素值的区域绘制出来，即提取所需研究的特征频率分布情况。对连通域面积进行求解就是对频率成分所占面积进行求解，该面积占全图面积比例即为特征面积比，用以表征故障情况。图11为对4组不同转速条件下的9个故障数据文件和一个正常数据文件进行验证分析所得结果。

图11 信号频率成分分布比例图Fig.11 Signal frequency component distribution proportion chart

分析图11所示实验结果，可初步设定频率成分所占比例10%以上为正常信号，信号频率成分所占比例低于10%则为故障信号。

4.4.2 诊断效果

实验对每一个数据文件进行再采样，得到100个数据样本。针对4种转速、9种故障情况下的故障数据及4种转速下的正常信号，总共得到4 000个样本数据。经实验验证，正确诊断的数据样本数为3 504，本方法的诊断正确率可达87.6%。该方法能对不同长度、不同采样频率的振动信号数据进行分析，具有较强的适应性，处理过程对信号特征进行可视化处理及特征强化，具有高透明性，且能较快地计算出判断依据，得出判读结果。

5 结论

1）将时域信号转换到时频域上，以热力图的形式结合图形学，可对频率分布特征进行强化，可对机械振动信号进行表征；

2）通过分析信号各频率成分在图像中的像素分布情况可以得出结论，能通过各频率成分在整个时频域中的面积占比情况来表征机械故障信息。最后通过特征面积比实现机械故障诊断。该方法的时间复杂度较低，诊断过程清晰直观，诊断效果较好，可以为机械故障诊断提供新思路。