一类超混沌系统的动力学分析及电路实现

宋 爽，汤 琼，瞿民凯，赵思远

（湖南工业大学 理学院，湖南 株洲 412007）

1 背景知识

1979年，学者O.E.Rössler首次发现了一个可以同时产生两个方向上双曲不稳定的混沌奇异吸引子的四维动力学系统[1]，并将之命名为超混沌现象。相较于常见的三维混沌系统，超混沌系统在实际应用中更能满足通信保密、图像加密、人工神经网络、非线性电路等领域的需求。超混沌系统可以通过引入新的状态变量反馈或基于忆阻器元件实现，得到四维及以上的高维动力学系统[2-5]，并通过改变非线性项取值范围或忆阻器的控制参数，获得倍周期分叉、单涡卷吸引子、双涡卷吸引子、单方向多涡卷吸引子，甚至网格多涡卷吸引子等混沌现象，现已成为混沌系统中极具研究价值的一个方向。

相较于低维混沌系统较为简单的动力学特性和不够多的密钥参数，超混沌系统具有更复杂的动力学特性和更丰富的密钥参数。判定一个动力学系统是否为超混沌系统，最直观的判断标准就是具有两个或两个以上的正Lyapunov指数。

近几十年来，国内外学者一直在研究生成超混沌系统的方法。受学者Li Q.D.[6]发现超混沌Chen系统的启发，科研工作者们多通过引入新状态变量反馈法生成超混沌系统[7-14]。由于引入状态变量的反馈控制器多为非线性项，它可进一步丰富动力学系统的混沌特征，增加系统的不可预测性。该系统的电路实现取决于反馈量非线性项的复杂程度，如何找到简单且易实现的超混沌系统一直是混沌电路的研究目标。

虽然关于超混沌系统的构造已经有了大量的研究，但是由于混沌吸引子较为复杂的动力学特性，现有关于多涡卷混沌系统电路实现的报道仍然比较少。因此，对不同非线性控制函数构造的超混沌系统进行详细的动力学分析，并搭建出对应的电路模型，是十分必要的。因此，本研究在三维Lü系统[7]的基础上加以修改，构建了一个基于状态变量反馈的四维动力学系统，经计算Lyapunov指数后，证实其为超混沌系统。然后，对其进行了基本的平衡点稳定性分析、耗散性分析、对称性分析等动力学分析，并通过计算Lyapunov指数及维数、绘制Poincaré截面图等方法对该超混沌系统进行了数值仿真分析。最后，根据反相器、积分器等基本的运算放大电路搭建出其相应的电路模型。本研究基于忆阻器反馈设计新的超混沌系统，该方法在增加系统维度的同时丰富了系统的混沌特征，且对应的混沌电路设计更易实现，本研究可为混沌系统的电路实现提供参考。

2 超混沌系统的数学模型

在三维Lü系统基础上进行修改，构建了一个基于状态变量反馈的四维动力学系统，新的超混沌系统的状态方程如下：

式中：a、b、c、d、e、g均为实数，且a、b、c、d、e均为正实数，e为控制参数。

由式（1）可知，该混沌系统是基于状态变量反馈控制实现的超混沌系统。

当系统（1）取a=35、b=35、c=1、d=3、e=3、g=-27时，得到该超混沌系统的相轨迹图如图1所示。

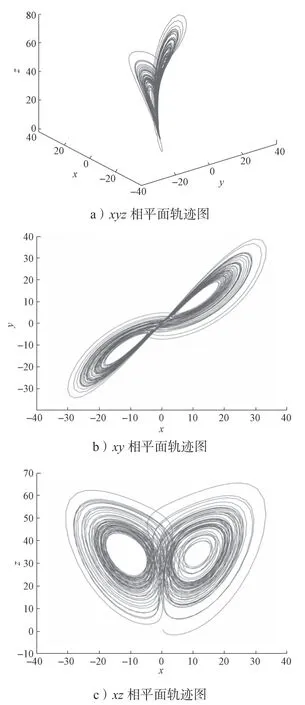
图1 超混沌系统（1）的相轨迹图Fig.1 Phase diagram of the hyperchaotic system (1)

通过观察图1所示超混沌系统的相轨迹图可以得知，该超混沌系统的涡卷数目为2个，有明显的混沌现象。

3 超混沌系统的动力学分析及数值仿真分析

3.1 超混沌系统的动力学分析

由于非线性混沌系统的解析解通常无法轻易获得，所以需要通过平衡点稳定性分析、耗散性分析等定性分析的方法获得系统的近似形态。

3.1.1 平衡点稳定性分析

对于一个四阶非线性自治系统，经平衡点线性化后得到其雅可比矩阵，根据解得的特征值性质的不同，会得到不同性质的平衡点。下面针对每一个平衡点逐一展开讨论。

令系统（1）的右边全部等于0，则可以得到如下方程组：

解得系统（1）的平衡点有两种情况：

1）d=0时，系统无平衡点；

2）d≠0时，系统存在平衡点P1（0, 0,, 0）。

3.1.1.1 系统（1）无平衡点时的超混沌吸引子

取a=8、b=0.1、c=1、d=0、e=2、g=-8时，初值为[0 1 1 0]时，系统（1）没有平衡点，且此时该新超混沌系统的Lyapunov指数为：

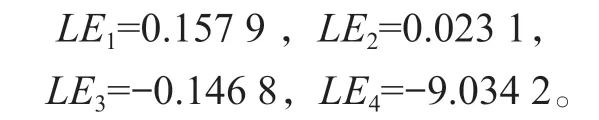
可见，系统（1）满足存在两个正的Lyapunov指数的条件，故该系统存在隐藏的超混沌吸引子，其相图如图2所示。

图2 系统（1）隐藏超混沌吸引子的相轨迹图Fig.2 Phase diagram of the hidden hyperchaotic attractor of system (1)

通过观察图2所示的相轨迹图可知，该系统有明显的混沌现象。

3.1.1.2 系统（1）有一个平衡点时的超混沌吸引子

当d≠0时，系统存在平衡点P1(0, 0,, 0)。其中，g可取任意实数，则该系统有无限平衡点集。在平衡点处做线性化处理，可得到系统（1）线性化后的雅可比矩阵为

将式（3）代入平衡点坐标后，令|λI-J|=0，则系统（1）在平衡点处线性化后得到的特征方程为

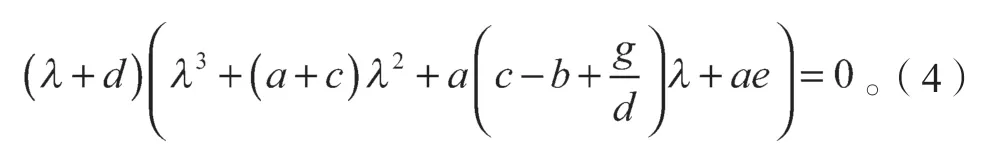
特征方程的第一个特征值为λ1=-d，设

则根据Routh-Hurwitz判据，可得：

则有

若系统（1）同时满足

当系统（1）取a=35、b=35、c=1、d=3、e=3、g=-27时，在平衡点P1处对系统（1）进行线性化处理后，求得对应特征方程（4）的解为

此时，特征方程（4）的解为两正两负的实特征值，且所有特征值之和满足λ1+λ2+λ3+λ4<0，故此时系统（1）的平衡点P1是具有二维稳定流形和二维不稳定流形的鞍焦平衡点。将此时系统（1）的各参数取值代入后，式子仍然成立，故P1是不稳定的鞍焦点，系统呈现超混沌现象，此时系统（1）的相图如图3所示，可见结果符合前文论述结论。

图3 系统（1）有一个平衡点时的超混沌吸引子相轨迹图Fig.3 Phase diagram of the Hyperchaotic system (1)with an equilibrium point

3.1.2 对称性分析

对于超混沌系统（1）做(x,y,z,w)～ (-x, -y, -z,-w)变换后，发现该系统的状态方程仍保持不变。故该系统关于z轴对称，且这种对称关系对于系统的所有参数都成立。

3.1.3 耗散性分析

系统（1）的相空间容积率为

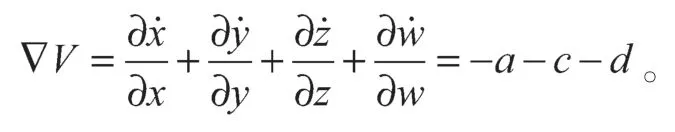
当a-c-d<0时，系统是耗散的，相空间的体积元将以指数形式收敛：

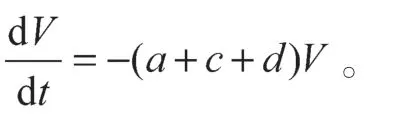
解得V=V0e-(a+c+d)t。

即当时间趋近于无穷大时，系统的每一条轨线都将以-(a+c+d)的速度指数收敛至0。最终，系统的所有轨线收敛至体积为0的集合，系统的所有轨线都固定于一个吸引子上。

当系统（1）取a=35、b=35、c=1、d=3、e=3、g=-27时，=-(35+1+3)=-39<0，即此时的系统（1）是耗散的。

3.2 超混沌系统的数值仿真分析

由于混沌系统的解对初值具有敏感依赖性，从而很难证明所获得的近似解是否会收敛于系统的真实解。因此，除了对系统进行定性分析之外，还需要通过数值分析方法，如Lyapunov指数谱、Poincaré图等，对混沌系统进行进一步的定量分析，以弥补定性分析的某些不足，从而更全面地研究动力学系统的混沌特征。

3.2.1 Lyapunov指数谱及维数

当取a=35、b=35、c=1、d=3、e=3、g=-27时，可以计算得：

此时，系统（1）满足存在两个正的Lyapunov指数，处于超混沌状态，其Lyapunov指数图见图4。

图4 系统（1）的Lyapunov指数图Fig.4 Lyapunov exponential diagram of system (1)

Lyapunov维数计算公式为

其中，k满足以下条件：

将Lyapunov指数代入后算得，

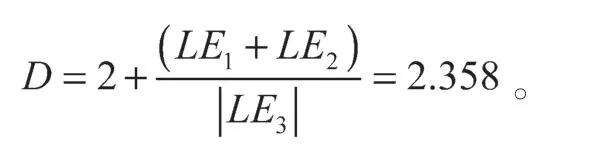
故可知该超混沌系统为分数维，具有丰富的动力学特性。

3.2.2 Poincaré截面图

当选取参数a=35、b=35、c=1、d=3、e=3、g=-27时，绘制出该系统的Poincaré截面图，如图5所示。

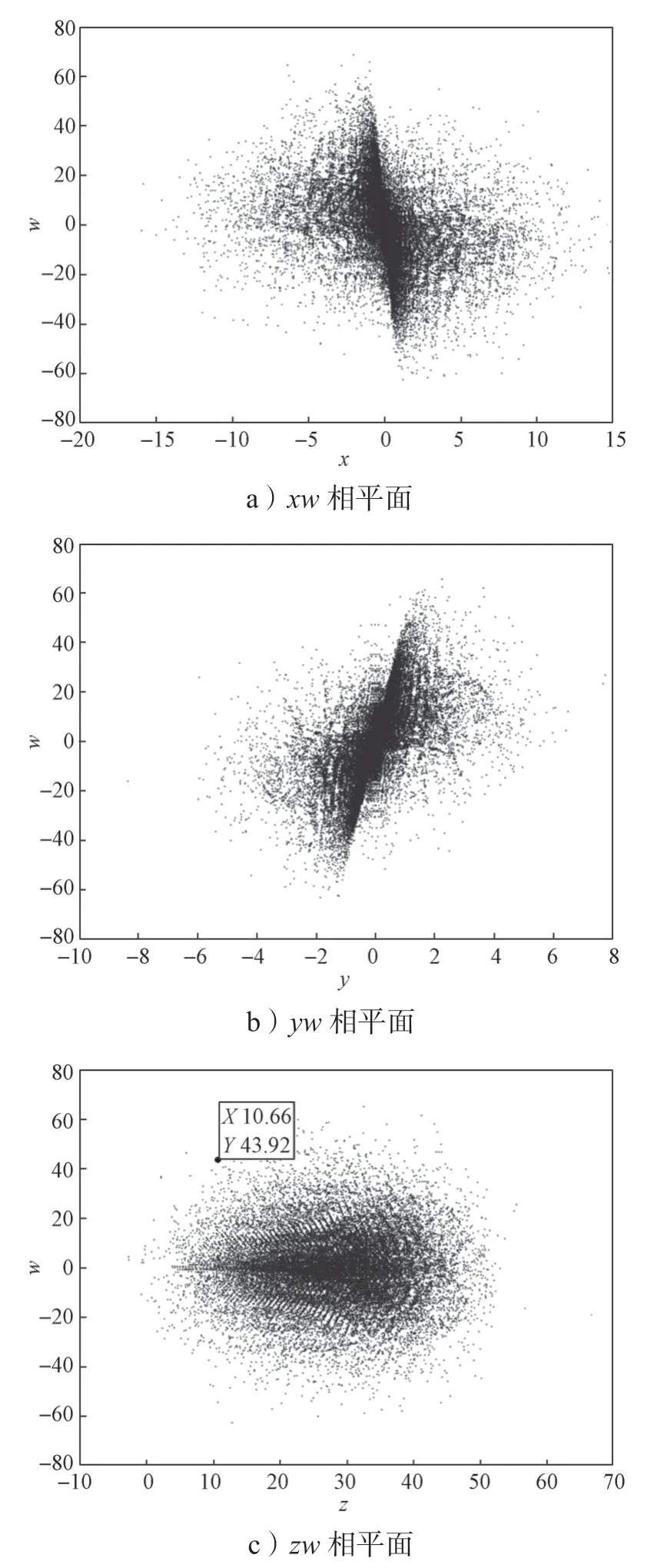
图5 系统（1）的Poincaré截面图Fig.5 Poincaré diagram of system (1)

观察图5所示的系统（1）Poincaré截面图可以发现，不论是yz相平面还是xw相平面的Poincaré截面图，上面都有着一片密密麻麻杂乱分布的点，结合该系统有两个正Lyapunov指数的特征，可以得知此时系统（1）处于超混沌状态。

4 超混沌系统的电路实现

本文采取模块化设计思路，运用简单的电感、电容、运算放大器等元件实现电路的搭建。

由于要运用到反相器等运算放大电路，需先将方程组（1）改写为

为了使信号在时域上扩展而幅度不发生变化，需要先对各变量取值范围进行核查，若各变量取值超过元件额定值，则需要对系统的状态方程进行时间尺度变换：

令τ=τ0，其中τ0是时间尺度变换因子，取τ0=100 μs，则方程组可改写为

根据式（7），可搭建出其对应的输出为x、y、z、w的电路图，如图6所示。

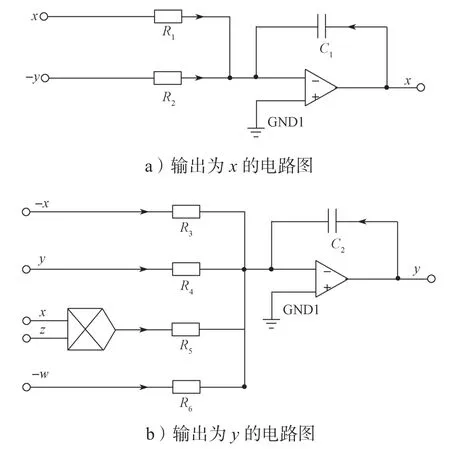
图6 系统（1）的Simulink电路图Fig.6 Simulink simulation circuit of system (1)

图6中，当运算放大器工作于线性状态时，其两个输入端可视为等电位。由于运算放大器的差模输入电阻较大，故流入运算放大器输入端的电流可以小到忽略不计，即可以将运算放大器的两个输入端视作开路，得到：

图中的电容是为了避免因参数选取过大导致进入混沌前时间过长，特选取C1=C2=C3=C4=100 nF，比较式（7）和（8），可得：

解得：R1=R2=R3=2.86 kΩ，

R4=R6=R7=100 kΩ，

R5=R9=0.1 kΩ，

R8=R10=33.33 kΩ。

故可得系统（1）的电路图如图7所示。

图7 系统（1）的电路图Fig.7 Circuit realization diagram of system (1)

5 超混沌系统电路的仿真验证

为了证明设计电路的正确性，在Simulink中搭建了对应的模拟电路。本文采用了模块化设计的思路，运用运算放大器、电容、电感等基本元件组成反相器，与积分器一起搭建出模拟电路。其中，给定运算放大器的门限电压设置为±15 V，考虑到乘法器AD633JN的乘法因子为0.1/V，R5、R9的取值变更为1 kΩ，并按照计算出的参数设置元件的值，观察示波器输出的结果，所得仿真结果如图8所示。

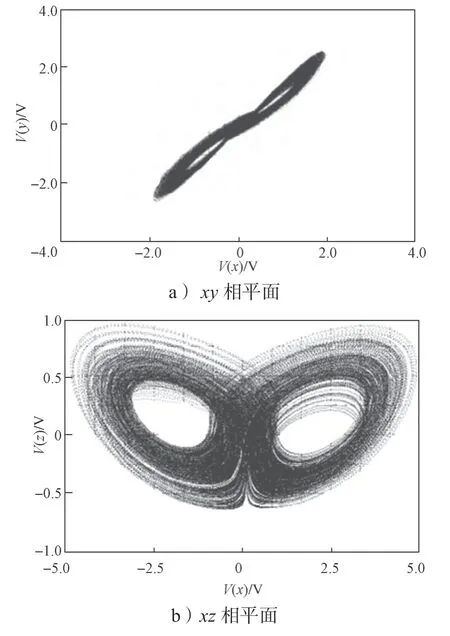
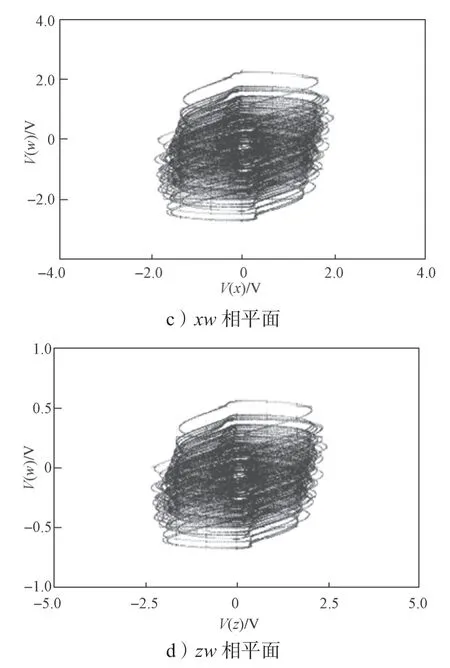
图8 系统（1）的Simulink仿真结果图Fig.8 Simulation diagrams of system (1)

将图8所示仿真结果与吸引子相轨迹图进行对比，发现该超混沌电路的实验结果与Matlab的数值仿真结果一致，这证明所设计的电路准确有效。

6 结语

相比于常见的三维混沌系统，超混沌系统有着更为复杂的混沌特征，更能满足现代通信保密、图像加密、人工神经网络、非线性电路等领域的需求。如何找到结构简单、动力学特性丰富的超混沌系统，并且将其应用到实际生产与生活中，是混沌理论一直追求的目标。

本文采用状态变量反馈法构造了一个新的超混沌系统，通过根据平衡点对应的雅可比矩阵计算出相应的特征值判定平衡点的稳定性等定性分析方法，以及计算Lyapunov指数和维数、绘制Poincaré截面图等定量分析方法，对超混沌系统进行了基本的动力学分析。通过基本的运算放大电路，搭建了新超混沌系统的电路模型，并利用Matlab-Simulink仿真模块库验证了电路实现的准确性，为超混沌系统的研究提供了新的思路。