基于柔性轮轨模型的车轮谐波磨耗对高速轮轨系统振动影响的仿真研究
胡晓依,侯银庆,宋志坤,成 棣,侯茂锐
(1.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心,北京 100081;2.北京交通大学 机械与电子控制工程学院,北京 100044)
车轮谐波磨耗又称车轮多边形,是车轮踏面缺陷最常见的形式之一,普遍存在于地铁及高速列车运营过程中[1-2]。而高速动车组车轮谐波磨耗引起的主要振动频率一般在500 Hz以上。针对车轮谐波磨耗引起的高频振动,国内外学者进行了大量的研究。NIELSEN[3]针对车轮失圆状态建立了数学模型并开发了计算机程序用于模拟车轮多边形对轮轨接触力和车辆/轨道响应的影响。JOHANSSON等人[4]通过数值仿真和现场试验相结合的方法分析了非圆化车轮对轮轨垂向力的影响。WU Yue等人[5]采用现场试验的方式对车轮高阶多边形的形成机理进行了研究,结果表明构架耦合共振对车轮多边形的形成起到了关键的作用。吴越等人[6]通过仿真与试验结合的方法研究了车轮高阶多边形对轮轨间作用力和构架振动的影响。ZHONG等人[7]利用传统的动力学模型和动态系统模型,研究了在车轮谐波磨耗下轮对弯曲和车轮腹板轴向变形对轮轨滚动接触行为的影响。周新建等人[8]建立了基于Timoshenko梁钢轨的刚柔耦合振动模型,研究了车轮谐波磨耗高频振动对轮轨蠕滑特性的影响。宋志坤等人[9]通过SIMPACK动力学软件联合ANSYS有限元软件建立了基于柔性轮对的车辆耦合动力学模型,分析了车轮谐波磨耗对轮轨力的影响。通过以上学者的研究可以发现,基于柔性轮轨的动力学模型是车轮谐波磨耗研究发展的必然趋势,其不仅可以有效地提高计算效率,还可以使分析结果具有一定的可信度。但目前利用有限元软件与动力学软件联合建立柔性轮轨接触模型还不是十分成熟,大多数针对车轮高频振动的仿真分析建立的模型还是单独考虑轮对为柔性或者轨道为柔性,仿真研究时综合考虑轮对柔性和轨道柔性的还不多,这与实际情况存在一定的差异。
为了更加深入地研究车轮高阶谐波磨耗激励下轮轨柔性状态下的变形及轮轨系统共振对高速轮轨系统振动响应的影响,本文以某型高速动车组为研究对象,通过ANSYS软件和SIMPACK软件建立基于Timoshenko梁的柔性轨道和柔性轮对的车辆—轨道耦合动力学模型,对比验证建立柔性轮轨模型的必要性。通过对试验数据的统计与分析,选取4种典型的车轮谐波磨耗(阶次为18~21阶,幅值为0.01~0.04 mm)作为系统输入激励,基于柔性轮轨模型研究不同速度下车轮高阶谐波磨耗阶次和幅值对高速轮轨系统振动的影响。
1 车辆—轨道系统耦合动力学模型
1.1 轮对柔性化建模
轮对柔性化建模的关键是建立刚柔耦合的铰接点,并通过子结构分析得到轮对的模态信息。考虑到在ANSYS软件中建铰接点会影响子结构分析生成的模态信息,因此采用SIMPACK软件中的自定义编辑参考点法建立刚柔耦合铰接点。SIMPACK中自定义铰接方法、ANSYS中刚性铰接方法与缩减前自由模态信息对比分析见表1,轮对3阶弯曲模态振型如图1所示。
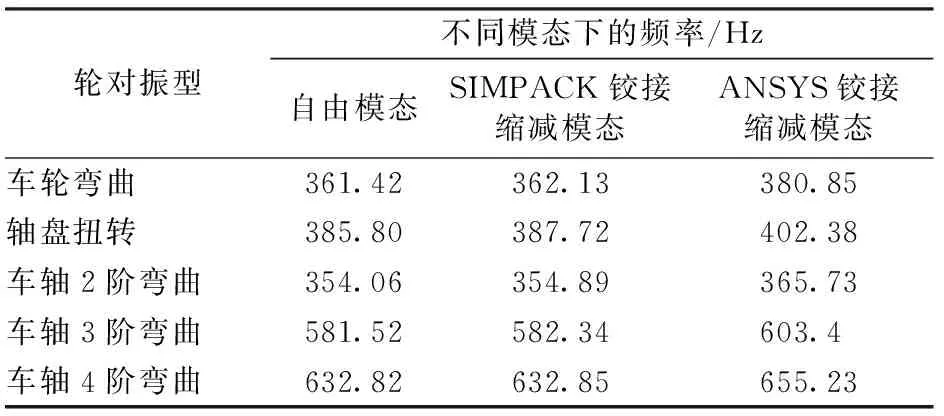
表1 高阶模态信息对比分析

图1 轮对三阶弯曲模态振型
从表1可知:SIMPACK中自定义刚性铰接缩减模态信息与缩减前相差最大不到0.5%,而通过Mass点在ANSYS中建立刚性铰接点时最大模态偏差达到16.58 Hz,误差率达到4.3%,对计算结果存在一定的影响。
1.2 轨道柔性化建模
轨道的柔性化建模与轮对柔性化的建模存在较大的差别。利用SIMPACK软件进行轮轨系统刚柔混合动力学建模时,柔性轨道在导入SIMPACK软件前采用MATLAB软件编写柔性轨道的配置文件,通过读取配置文件将柔性轨道导入到SIMPACK软件中。建模时将柔性轨道视为等间隔支承基础上的Timoshenko梁,轨枕、道床等轨下部分等统一采用弹簧阻尼元件模拟,钢轨两端采用大刚度大阻尼进行强约束。轨上部分的轮对、轴箱、构架及车体视为移动载荷作用在钢轨上,其钢轨在移动载荷作用下的垂向变形示意图如图2所示。图中:mw为轮对质量;mb为一系簧上质量块的质量;Zb为一系簧上质量块的垂向位移;l为轨枕间距;Zw为轮对的垂向位移;Fr为轨下约束的支撑反力;Cp,Kp分别为一系阻尼和刚度;Cr,Kr分别为轨下阻尼和支撑刚度;Ft为轮轨垂向力。
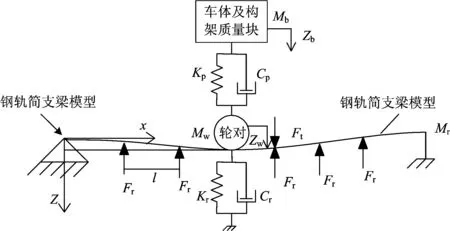
图2 钢轨振动的数学模型
假设车辆以均匀速度v运行时不发生跳轨现象即轮轨力不为零,将轨上部分视为移动载荷作用在视为简支梁的钢轨上,轨下约束的支撑反力由弹簧和阻尼元件产生,则钢轨所受外力可表示为
(1)
(2)
其中,
σZ(t)=Zwj(t)-Zr(xj,t)-Zx(xj,t)
式中:xi为钢轨纵向位置;t为时间;σZ(t)为轮轨间的弹性压缩量;Zr(xj,t)为第j位轮对下钢轨的垂向位移;Zx(xj,t)为第j位轮对下钢轨的轨道不平顺;G为轮轨接触常数。
在不考虑剪切刚度的情况下,钢轨的振动微分方程可表示为式(3),将钢轨的振型函数带入后可得其固有角频率为式(4)所示[10]。
(3)
(4)
式中:EI为钢轨抗弯刚度;N为参振轨枕数目;δ为Diracδ函数;ω0为振动频率;lr钢轨长度。
而实际情况中,钢轨由于受到扣件的压力作用及轨下支撑刚度的作用,钢轨在振动过程中容易被激发的频率是振型长度为轨枕间距的pinned-pinned固有频率,其约束状态下的垂向弯曲振动频率可由MAN A P D[11]改进的pinned-pinned振动频率估算公式进行计算。
(5)
式中:l为轨枕间距。
式(5)中,l=0.63 m,截面抗弯刚度EI=6.62 MN·m2[12],钢轨重量mr=60 kg·m-1,计算可得钢轨的pinned-pinned弯曲共振频率为990.27 Hz。
1.3 整车模型建立
为了研究柔性轮轨模型与其他3种模型(刚性轮轨模型、柔性轨刚性轮模型、柔性轮刚性轨模型)的区别,分别建立4种模型,分析不同模型下车轮高阶谐波磨耗对高速轮轨系统振动响应的影响。整车建模时将车体和构架考虑为多刚体,一、二系减振器统一采用弹簧阻尼元件代替,建立的整车模型如图3所示。其中将轨道考虑为柔性时,采用三维的弹簧力元对轨枕进行模拟,具体参数见表2。
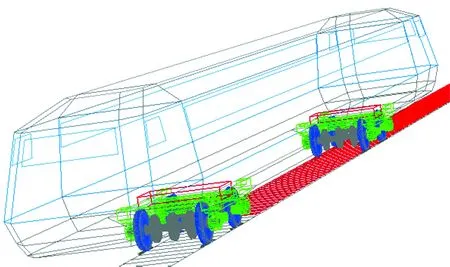
图3 车辆轨道动力学模型
2 轮轨耦合振动响应分析
车辆—轨道系统的耦合关系,体现为轮轨之间的相互作用关系,其核心是轮轨力。对于多刚体轮轨力的计算可直接采用浮动参考坐标法[13],通过各参考系之间的运动关系计算轮轨力。而柔性体耦合振动关系与多刚体存在一定的区别,SIMPACK软件中柔性轮轨的耦合需要通过建立无质量的虚钢轨与虚轮对耦合模拟柔性轮轨的几何接触,再运用虚功原理将柔性轮对与柔性轨道考虑成1个柔性体耦合的集合,将其与固化的参考点有限元模型进行耦合,通过计算各耦合点之间的运动关系描述轮轨力。

表2 计算参数设置
2.1 车轮谐波磨耗数据分析
通过对某型服役高速动车组车轮谐波磨耗进行的长期跟踪测试,得到该动车组9车1位车轮镟修后13.1万km时的实测结果如图4(a)所示。由图可知,左、右轮均出现了明显的谐波磨耗。车轮谐波磨耗阶次谱如图4(b)所示。由图可知,左右轮均出现了由20阶次主导的谐波磨耗。
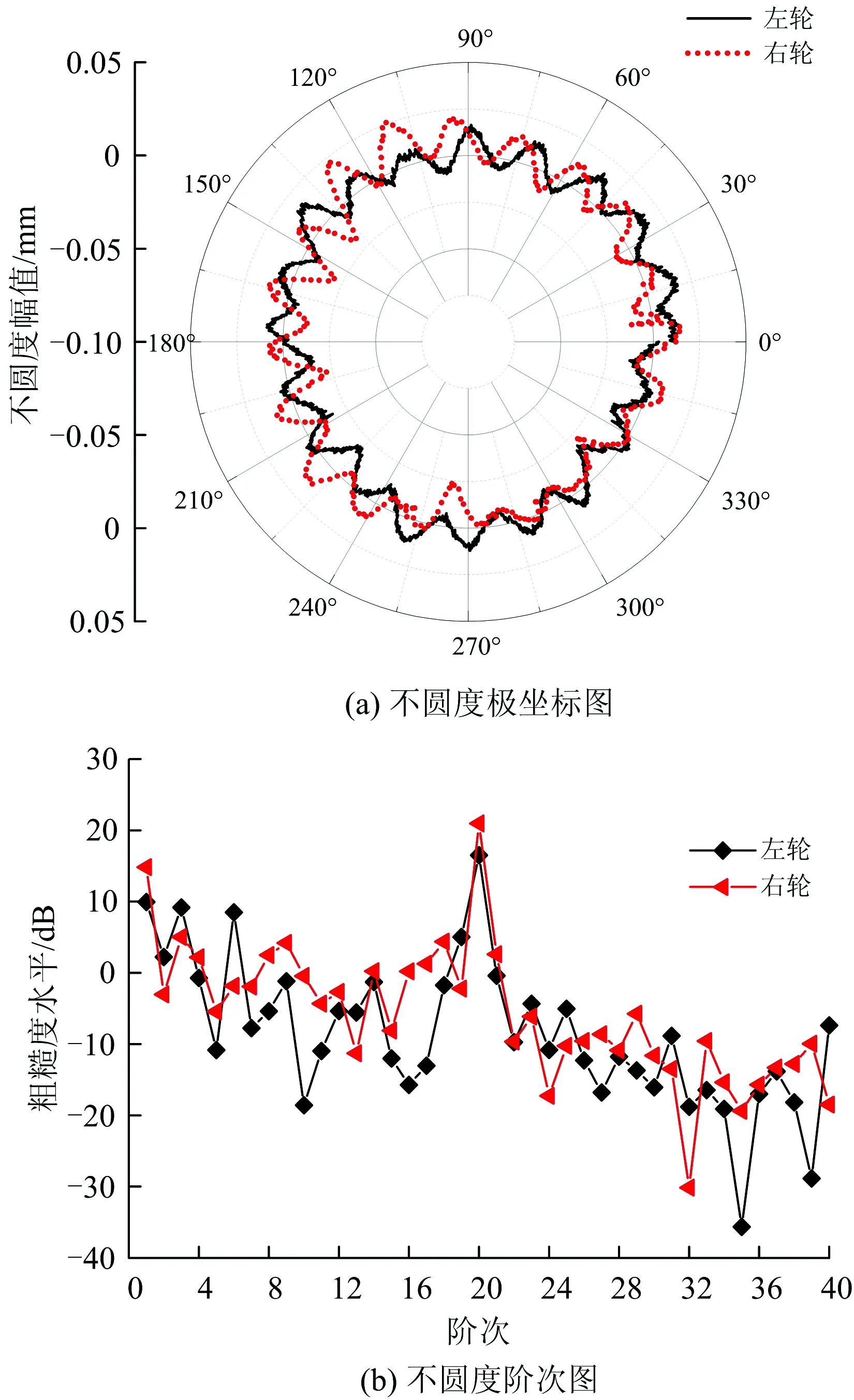
图4 车轮谐波磨耗实测结果
在仿真中,为了抓住主要矛盾,将实际车轮谐波磨耗形状简化为理想化的单一谐波形状进行研究,分别计算不同阶次下的轮轨系统振动响应。简化处理后理想化的19,20阶次车轮谐波磨耗如图5所示。
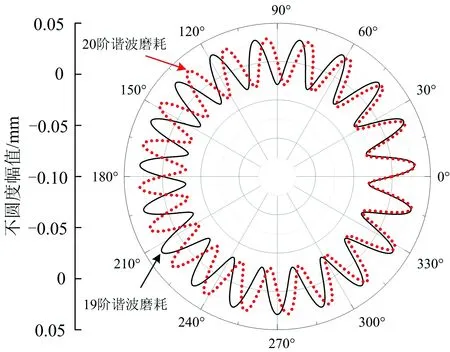
图5 理想状态下车轮谐波磨耗的数学模型
2.2 刚柔耦合振动对比分析
将实测的车轮谐波磨耗转化成理想的谐波激扰输入到动力学模型中进行仿真分析。考虑到柔性体与多刚体的主要区别在于结构体是否存在弹性变形和弹性模态,因此,为了分析不同模型之间的差异,设定车辆运行速度为300 km·h-1、轮径为920 mm、车轮谐波磨耗为20阶仿真工况。在该工况下,车轮谐波激励频率接近轮对3阶弯曲频率,仿真模型振动输出响应能很好反映出不同模型之间存在的差异。
车轮谐波磨耗幅值为0.01 mm时,基于不同模型计算获得的轮轨垂向力时、频图和轴箱振动加速度时程图分别如图6(a),(b)和(c)所示。
由图6(a)和(b)可以看出:在该谐波磨耗的激励下,基于多刚体、柔性轮刚性轨、柔性轨钢性轮、柔性轮轨模型计算出的轮轨垂向力最大值分别为102.06,107.37,85.70和90.41 kN。同为考虑轨道为刚性时,考虑轮对为柔性时计算结果比考虑轮对为刚性时大5.31 kN,相对增幅为5.2%;同为考虑轨道为柔性时,考虑轮对为柔性时计算结果比考虑轮对为刚性时大4.71 kN,相对增幅为5.5%。轮对是否为考虑柔性对轴箱振动加速度的影响非常大,由图6(c)可知,轮对考虑为柔性时计算得到的轴箱振动加速度约为考虑轮对为刚性时的4倍。同为考虑轮对为柔性时,考虑轨道刚性试计算得到的轮轨垂向力比考虑轨道为柔性时大17.67 kN,相对增加了19.7%。由此可以看出,同等情况下考虑轨道为柔性时计算得到的轮轨垂向力小于考虑轨道为刚性时的计算结果。造成此计算结果差异的原因在于,当轨道考虑为柔性时,由1.2节可知钢轨垂向pinned-pinned共振频率为900 Hz以上,车轮多边形激扰频率远离pinned-pinned共振频率,不会引起轨道pinned-pinned共振,可有效缓冲轮轨间的高频冲击振动。但轨道模型相同时,考虑轮对为柔性时计算得到的轮轨垂向力要大于轮对考虑为刚性时的计算结果。造成此计算结果差异的原因在于车轮20阶谐波磨耗引起的激扰频率为576 Hz,与轮对的3阶弯曲振动模态频率582.34 Hz接近,激起了轮对3阶弯曲振动模态,系统产生共振,由此导致轮轨垂向力增大。同时该共振也是导致图6(c)中轮对考虑为柔性时计算得到的轴箱振矾加速度约为考虑轮对为刚性时的4倍的重要原因。
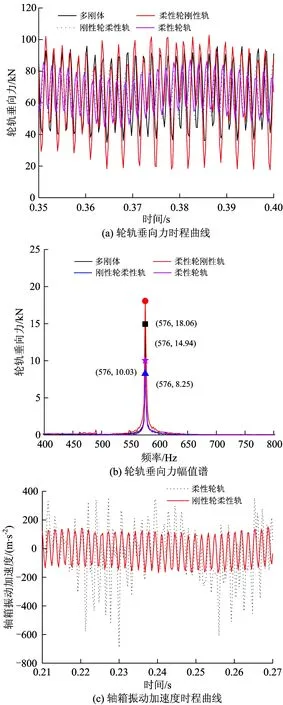
图6 20阶车轮谐波磨耗激励下轮轨垂向力及轴箱振动加速度时、频图
由以上分析可知,在仿真建模计算高阶谐波磨耗对高速轮轨系统振动影响时,同时将轮对及轨道考虑成柔性,可使仿真结果更接近实际情况。
3 基于柔性轮轨模型的轮轨振动响应仿真分析
为了研究柔性轮轨模型下,车轮谐波磨耗对轮轨垂向力、钢轨振动及轴箱振动加速度响应的影响,选取了18~21阶谐波钮耗车轮,对比分析了不同幅值(0.01~0.04 mm)、速度(200~350 km·h-1)下的振动响应情况,同时对其主导阶次的波深限值进行了分析。分析时取1位轮对处的右轮、右轨和右轴箱为响应输出测点。20阶谐波磨耗下不同速度引起的激励频率及300 km·h-1下不同车轮谐波磨耗阶次引起的激励频率分别见表3。
3.1 谐波磨耗对轮轨垂向力的影响
为了研究车轮谐波磨耗对轮轨动态相互作用关系,分别对车轮谐波磨耗下不同幅值、速度、阶次引起的轮轨垂向力变化规律进行了分析。
考虑车轮速度为300 km·h-1、车轮轮径为920 mm、车轮谐波磨耗阶次为20阶时,基于柔性轮轨模型得到的不同谐波磨耗幅值下轮轨垂向力变化的时程曲线如图7所示。
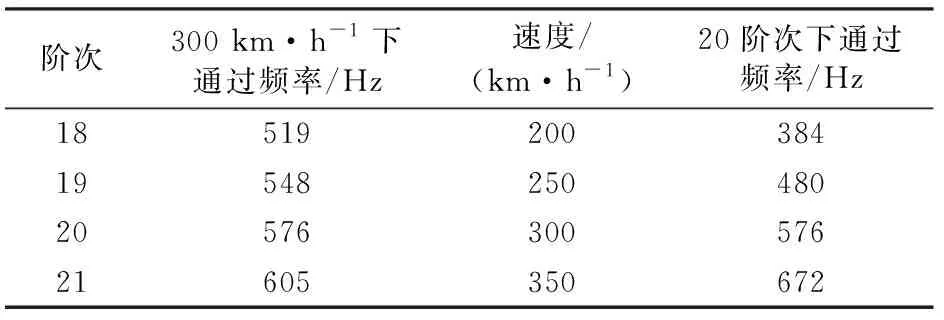
表3 不同阶次及速度下的车轮谐波磨耗的激励频率
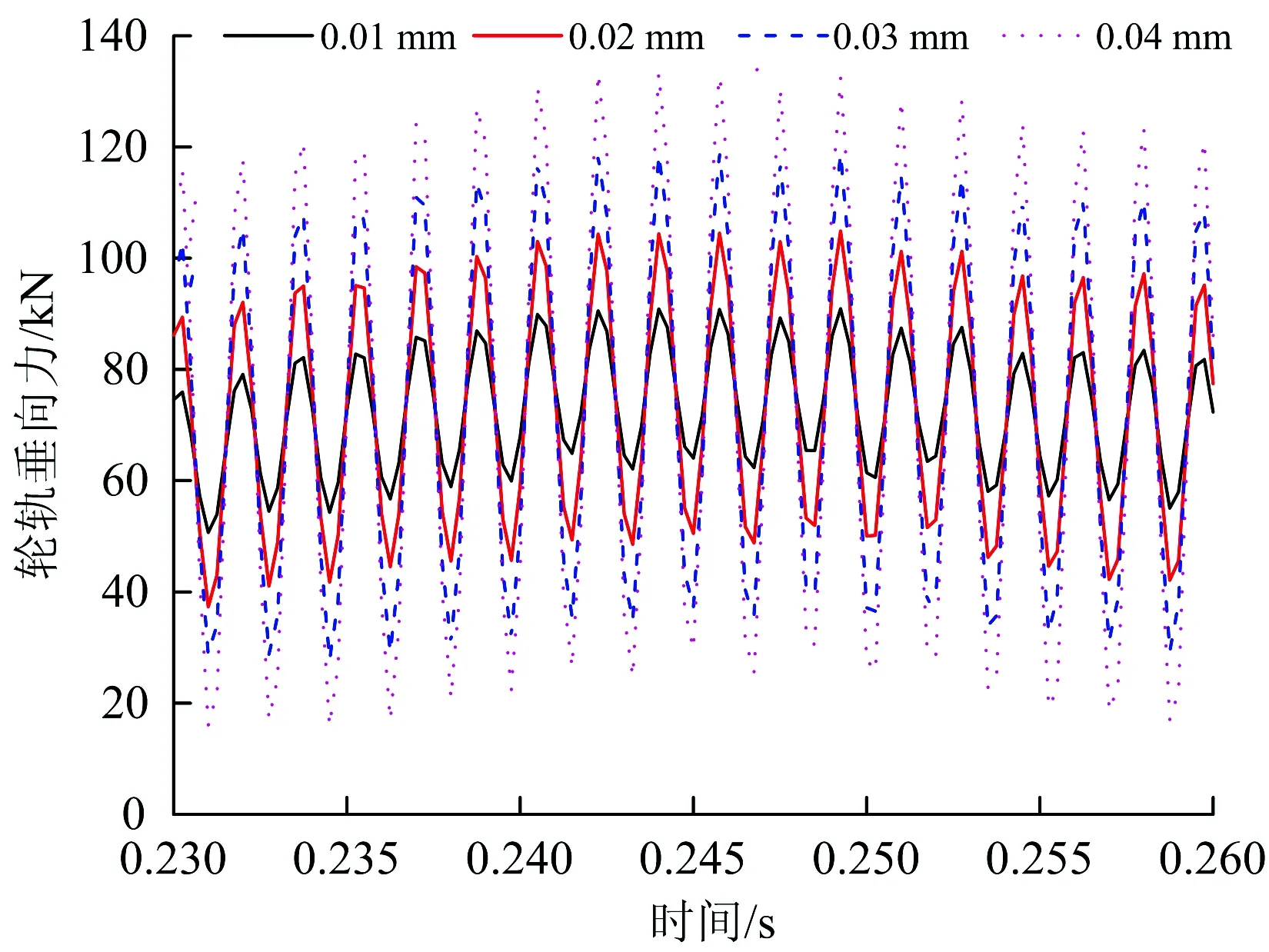
图7 基于柔性轮轨模型得到的不同谐波磨耗幅值下轮轨垂向力时程曲线
其中车轮谐波磨耗在该速度及阶次下的不同模型确定的幅值限值见表4。考虑车辆速度为300 km·h-1、车轮轮径为920 mm、车轮谐波磨耗阶次为20阶时,按不同轮轨模型计算得到的谐波磨耗幅值下轮轨垂向力最大值见表4。

表4 磨耗幅值0.01~0.07 mm下20阶车轮谐波磨耗轮轨垂向力最大值
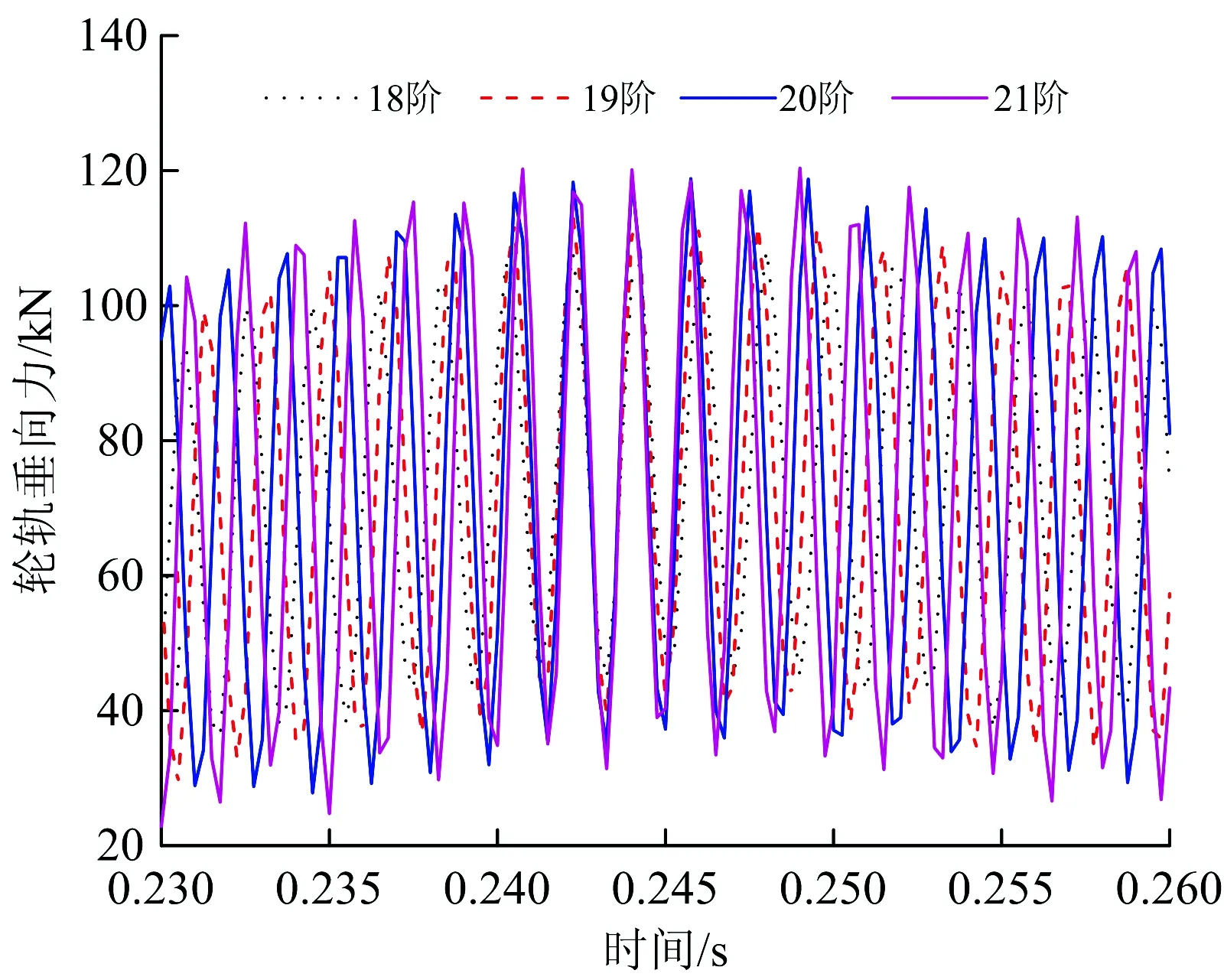
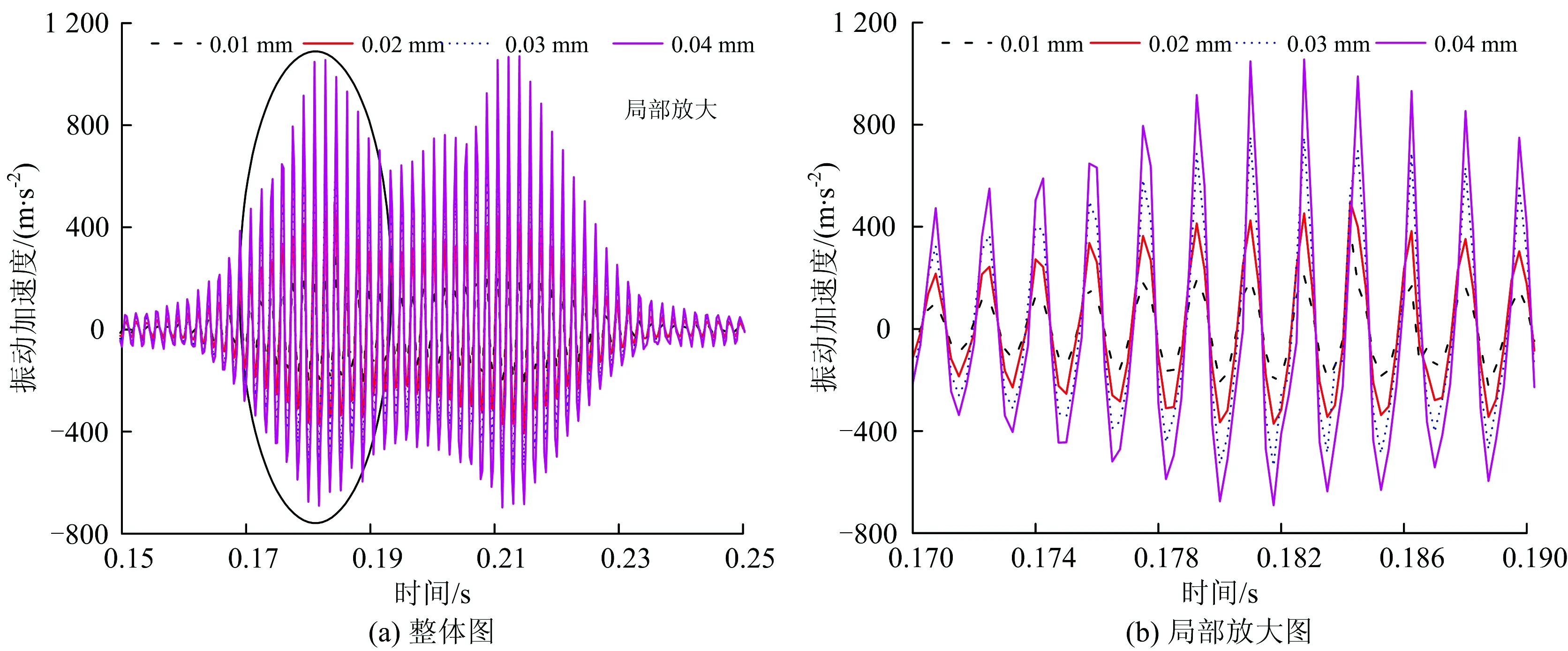
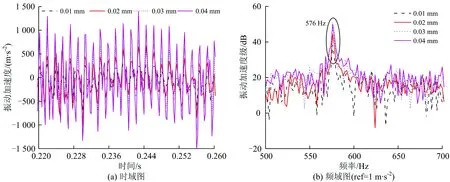
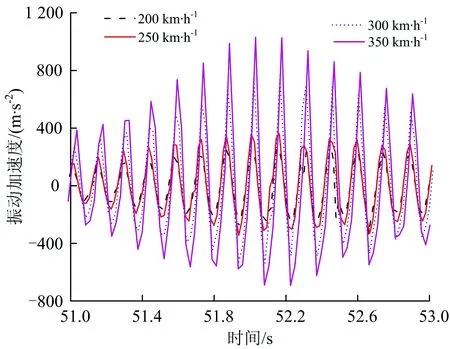
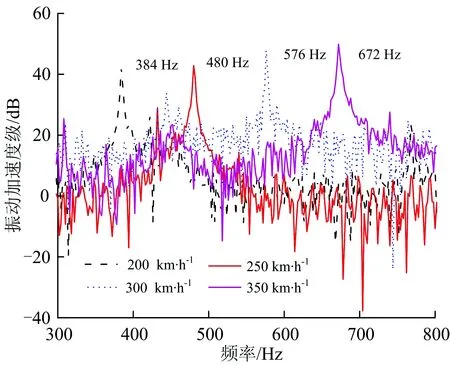
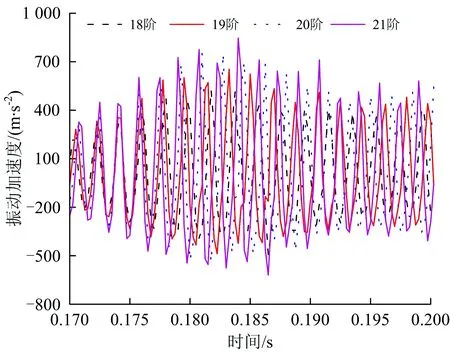
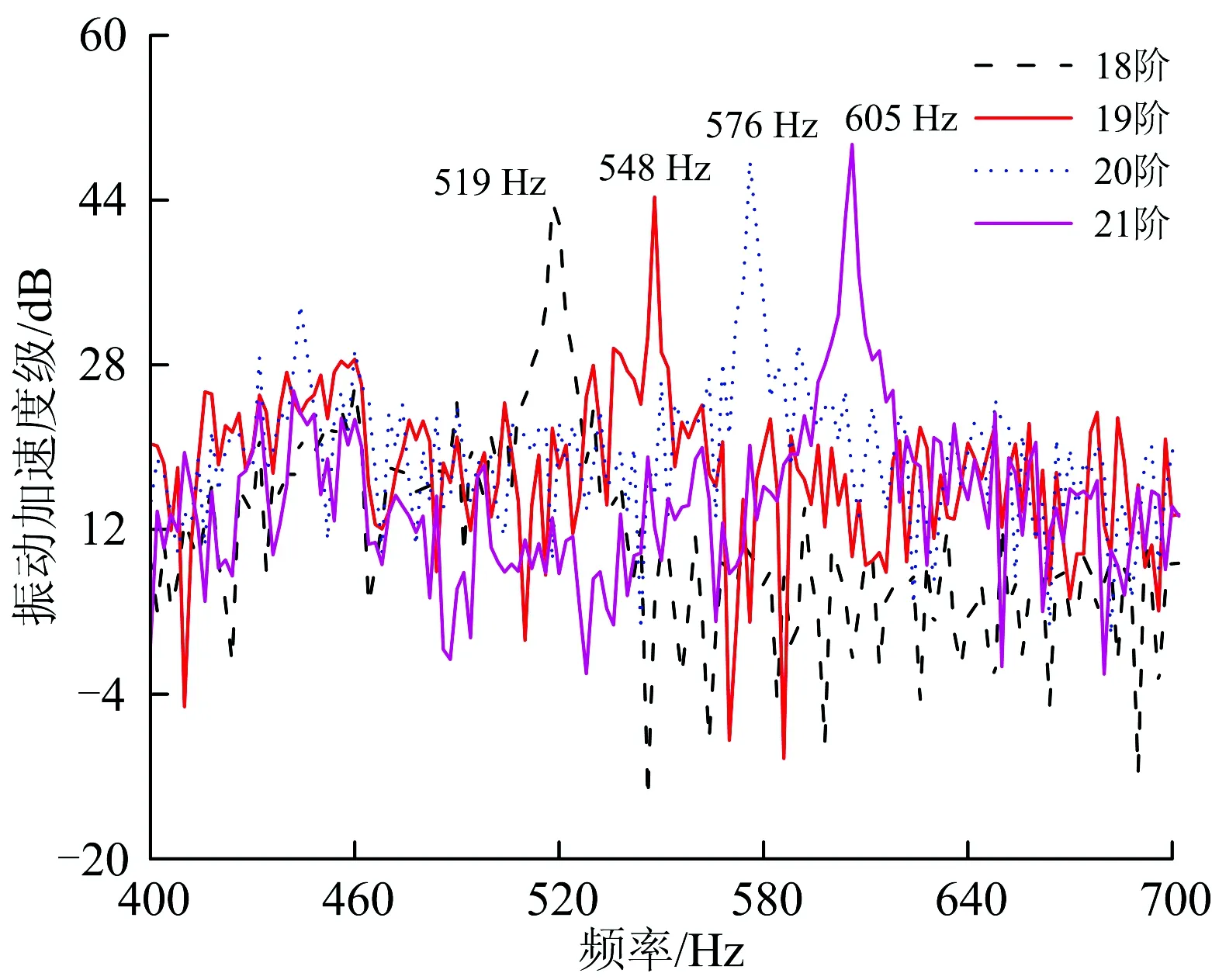
由图7和表3可知:在以上仿真工况下,轮轨垂向力随着多边形的幅值增大而增大,且基本呈等幅增大趋势;不同模型下轮轨垂向力增加幅值存在一定的差异,轨道考虑为柔性时,谐波磨耗幅值每增加0.01 mm,轮轨垂向增加约为4.5 kN左右;轨道考虑为刚性时,谐波磨耗幅值每增加0.01 mm,轮轨垂向增加约为28 kN左右。按照国际铁路联盟UIC—518《轨道车辆动力学性能试验及验收—运行安全性—轨道疲劳—乘坐舒适性》动力学标准中规定:轮轨垂向力限值为0 下面以车轮谐波磨耗幅值为0.03 mm为例,分别研究20阶车轮谐波磨耗下速度对轮轨垂向力的影响以及在速度300 km·h-1下阶次对轮轨垂向力的影响,分别如图8和图9所示。 由图8、图9可知,轮轨垂向力基本随着速度和阶次的增加而增加。从图8可看出,200 km·h-1下轮轨垂向力与250 km·h-1时下的轮轨垂向力相差较小,造成此差异小的原因是在该速度下车轮谐波磨耗的激励频率激发了轮对350~380 Hz左右的模态,引起共振。而300 km·h-1相对250 km·h-1下的轮轨垂向力变化较大的原因是在该速度下车轮谐波磨耗的激励频率接近轮对的3阶弯曲振动频率,激发了轮对3阶弯曲模态。由图9可以看出,20阶与21阶车轮谐波磨耗的激励下轮轨垂向力基本相等,造成此的原因同样是20阶车轮谐波磨耗激励激发了轮对的3阶弯曲模态,引起共振。总体来说,车轮谐波磨耗阶次从18阶变到21阶对轮轨垂向力影响较小,车轮谐波磨耗阶次相对于谐波磨耗的幅值和车辆运行速度对轮轨垂向力影响较小。 图8 速度对轮轨垂向力的影响 图9 阶次对轮轨垂向力的影响 车轮高阶谐波磨耗不仅对轮轨间的作用力产生影响,对钢轨及轴箱的振动也产生了显著的影响。在对服役动车组跟踪测试时,轮轨力不易直接测量得到,所以钢轨及轴箱等结构部件的振动加速度作为评价车轮多边形影响的重要指标。 下文分别研究车轮谐波磨耗对钢轨振动加速度和轴箱振动加速度的影响。 前转向架上不同幅值的多边形轮对以300 km·h-1的速度通过右轨上2个轨枕跨中节点引起的振动加速度响应仿真结果,及1位轮对通过跨中节点引起的振动加速度局部放大图如图10所示。该速度及阶次下不同幅值的谐波磨耗对轴箱振动加速度变化规律的时频曲线如图11所示。 由图10和图11可知,钢轨及轴箱振动加速度均随着车轮谐波磨耗幅值的增大而增大。当前转向架的4个车轮均存在谐波磨耗时,其中一侧车轮在通过钢轨跨中节点时,振动加速度整体呈现出先增大后减小的趋势。其中前轮通过后钢轨振动加速度会略微衰减,直到后轮通过后才完全衰减。由图11(b)可以看出,其振动主频与表2中计算的通过频率一致,均为576 Hz。0.04 mm幅值下钢轨的振动加速度峰值为1 070.98 m·s-2,轴箱振动加速度峰值为1 499.18 m·s-2,分别约为0.01 mm幅值下钢轨及轴箱振动加速度峰值的2.5倍。 图10 不同波深下钢轨垂向振动加速度时程曲线 图11 不同幅值下轴箱垂向振动加速度时、频图 谐波磨耗阶次为20阶、幅值为0.03 mm下,高速动车组运行速度为200~350 km·h-1时,前构架右侧前轮通过钢轨跨中节点时钢轨振动加速度响应的时程曲线如图12所示,相应轴箱振动加速度的频谱图如图13所示。 图12 不同速度下钢轨振动加速度时程曲线 由图12和图13可知,钢轨及轴箱振动加速度基本随着列车运行速度的增加而增加。其中200 km·h-1下钢轨振动加速度及轴箱振动加速度级与250 km·h-1下的振动加速度相差不大,造成此的原因,如前所述,200 km·h-1下的振动主频为384 Hz,激发了轮对350~380 Hz左右的模态,引起了共振。而300 km·h-1下的钢轨振动加速度及轴箱振动加速度级相比于250 km·h-1下的振动加速度增幅较大,同样如前所述,在300 km·h-1速度下车轮多边形激发了轮对的3阶弯曲模态,引起了共振。 图13 不同速度下轴箱振动加速度频谱图 速度为300 km·h-1时,车轮多边形幅值为0.03 mm下不同阶次对钢轨和轴箱振动加速度的影响分别图14和图15所示。 图14 不同阶次下钢轨振动加速度时程曲线 由图14和图15可知,车轮谐波磨耗的阶次对钢轨及轴箱振动加速度影响较小,其中21阶谐波磨耗下的钢轨振动加速度峰值相较于18阶下的钢轨振动加速度峰值增加了近1.6倍,轴箱振动加速度级增大了约5.7 dB。个别阶次相较于其他阶次增加较为明显,造成此的原因是在该阶次下,车轮多边形激励激发了轮对固有模态引起共振导致其振动幅值偏大。 图15 不同阶次下轴箱振动加速度频谱图 (1)仿真分析研究时,考虑轮轨均为柔性时能更真实地反应实际情况下的轮轨接触关系,使仿真分析结果更符合实际,从而为后续车轮多边形机理及控制对策的深入研究奠定了良好基础。 (2)同等情况下考虑柔性轨道柔性计算得到的轮轨垂向力小于考虑轨道为刚性时的计算结果。造成此的原因在于轨道垂向pinned-pinned共振频率为900 Hz以上,而计算的车轮多边形激励最大通过频率为672 Hz,不在其共振频率范围内。 (3)在同为考虑轨道为刚性或柔性的情况下,车辆运行速度300 km·h-1、车轮存在20阶谐波磨耗时,基于柔性轮对模型计算得到的轮轨垂向力比基于刚性轮对模型计算得到的值大。造成此的原因在于在该速度下20阶车轮谐波磨耗激励频率为576 Hz,激发了轮对的3阶弯曲模态,引起了共振。 (4)总体来说,车轮存在高阶谐波磨耗时,轮轨垂向力、钢轨及轴箱振动加速度响应随着多边形阶次、幅值及车辆运行速度的增大而增大,相比于谐波磨耗阶次对轮轨振动响应的影响,谐波磨耗的幅值对轮轨振动响应的影响程度更大。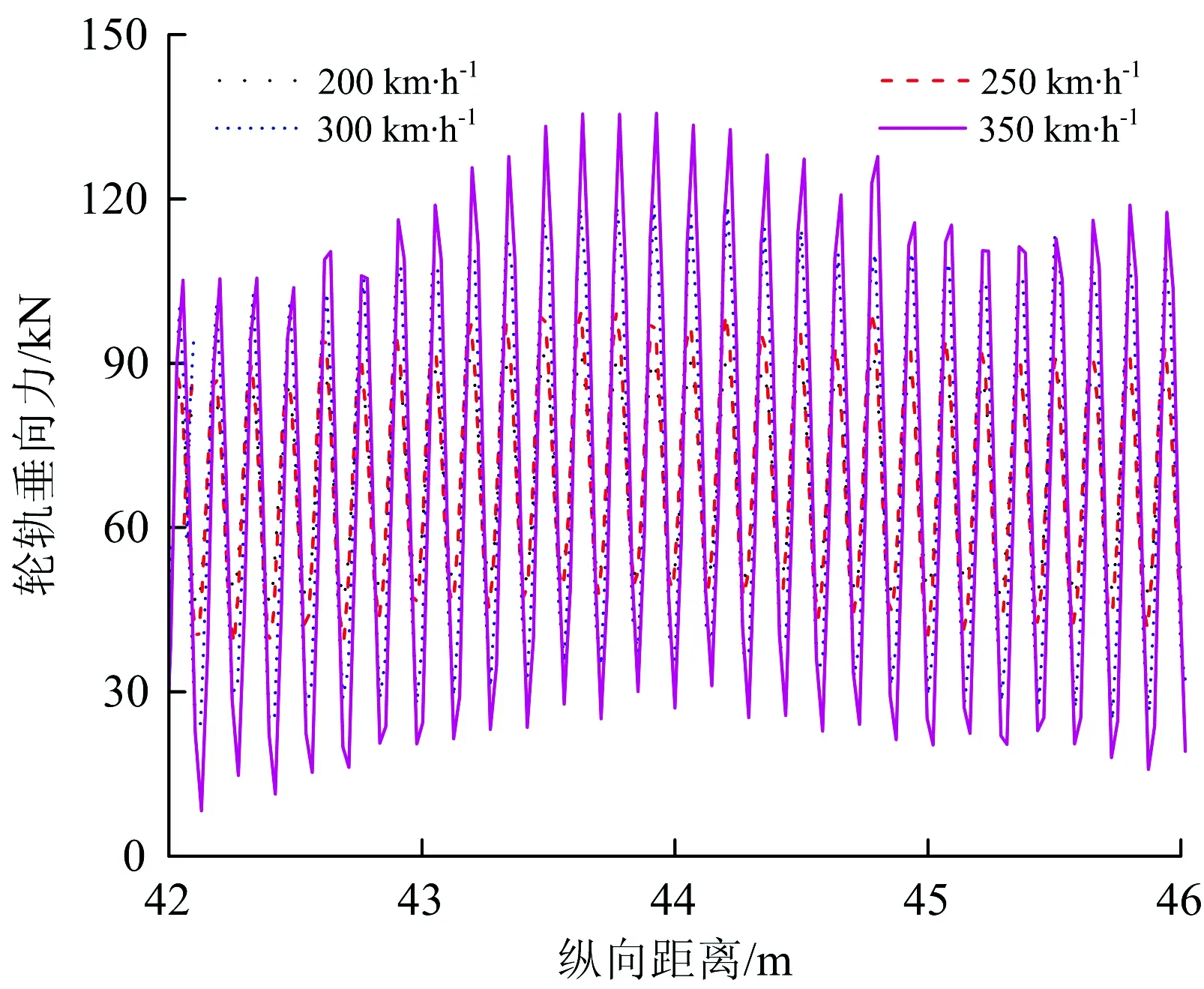
3.2 谐波磨耗对轮轨系统振动加速度的影响
4 结 论

