一类树型量子网络的非局域性

齐霄霏 ，杨丽华

（1.山西大学 数学科学学院，山西 太原 030006；2.运城学院 数学与信息技术学院，山西 运城 044000）

0 引言

在量子信息科学中，每个量子系统对应于一个复可分Hilbert空间H，H中的任意单位向量用表示。令B(H)表示H上所有有界算子构成的代数。称ρ∈B(H)为量子态，若ρ是迹为1的正算子。记H上全体量子态构成的集合为S(H)。特别地，称ρ∈B(H)为纯态，若其是秩一投影，即具有形如的形式，这里是H上的任意单位向量，表示的对偶向量；否则，称ρ为混合态。如果H=H1⊗H2⊗…⊗Hn是n个Hilbert空间的张量积，则称S(H)为n体复合量子系统［1］。

量子关联是量子力学区别于经典力学的主要特征，也是实现量子计算和量子通信的重要物理资源。作为一类重要的量子关联，量子非局域性一直是量子信息理论的核心研究课题之一。量子非局域性的研究起源于贝尔（Bell）的开创性工作［2］，其研究表明，量子世界所允许的测量结果之间的强关联性是不能够通过我们所熟悉的时空机制来解释的。量子非局域性的检测可以通过Bell不等式来鉴别，违反Bell不等式即意味着非局域性的存在（例如，可参见文献［3-7］及其参考文献）。非局域性的研究在量子密码学［8］、量子通信［9］等领域中有着非常广泛的应用。

量子网络是实现长距离、网络式量子通信的基础，它是通过量子节点来产生、处理和存储量子信息，利用飞行比特作为量子信道来传递信息的全量子信息处理与传输的网络系统，在量子计算、量子通信和量子测量中扮演重要角色。而量子网络区别于经典网络的主要特征之一就是量子节点之间具有非局域关联。近十年来，量子网络的非局域性研究受到越来越多研究学者的关注，成为热点课题之一，具有非常重要的科学意义和应用前景。

对于量子网络非局域性的研究，文献［10］给出了称作纠缠交换的实验，该实验说明其对应的量子网络中两个独立纠缠比特态通过进行适当的联合测量可以使非直接连接的系统之间产生非局域性。Branciard等人在文献［11-12］中对［10］中简单量子网络的非局域性进行了系统研究，发现对分别由两个独立资源S1，S2产生的隐态进行联合测量后可以产生关联，称为非双局域性（bilocality），并给出了双局域不等式。之后，对于不同类型量子网络的非局域性研究也得以逐步展开。例如，文献［13］证明了对于文献［12］中的简单链型网络，所有纠缠纯态均违背双局域不等式，进而都是非双局域的，同时也给出了混合态是非双局域的条件；文献［14-17］分别把简单链型量子网络的非局域性推广到n-链型量子网络与n-星型量子网络，并得到了不同的Bell型局域不等式；Renou等人在文献［18］中引入另一种类型的量子网络，即三角形网络，研究了该网络的三局域性。对于其他类型量子网络的非局域性研究，参见文献［19-24］。关于量子网络非局域性和传统Bell非局域性的关系，可参见文献［13，16］。

尽管关于量子网络非局域性的研究已取得许多深刻的成果，但是许多常见类型的量子网络，如树型量子网络等，还没有文献深入研究。树型量子网络被广泛应用在量子通信和量子模拟中［25-26］，因此研究这种网络的非局域性很有必要。本文将研究一类结构较简单的树型量子网络，其有13个观测者，共享12个两体的物理资源。本文第1节将给出该类树型量子网络满足的12局域不等式，第2节讨论第1节中所得局域不等式的量子破坏，证明了所有的纠缠纯态均破坏12局域不等式，从而是非12局域的。

本节最后给出量子测量的概念。假设H是有限维复Hilbert空间。对于A∈B(H)，A*表示A的共轭转置算子。特别地，若A=A*，则称A为自伴算子。自伴算子在量子信息中也被称为可观测量。量子测量由空间H上的一组测量算子{Mm}⊂B(H)描述，其满足完备性条件。投影测量是一类特殊的量子测量，其由一个可观测量M来描述。将M进行谱分解M=∑mPm，测量结果即为M的特征值m，测量状态时，得到结果m的概率为，测量后系统的状态为。

1 一类树型网络的12局域不等式

本节先给出本文研究的树型量子网络的结构（见图1）。

图1 树型量子网络，它包括12个资源和13个观测者Fig.1 The tree-tensor network，which consists of 12 sources and 13 observers

该网络由12个物理资源S1，…，S12和13个观测者A，B1，B2，B3，C1，C2，…，C9构成。假设12个物理资源是相互独立的，分别用隐变量λ1，…，λ12描述。此外，假设所有的观测者都有两个输入与相应的两个输出，分别记为x，y1，y2，y3，z1，z2，…，z9(∈ {0，1})与a，b1，b2，b3，c1，c2，…，c9(∈ {0，1})。若对于13个观测者的所有输入和所有输出，其所产生的联合概率分布满足下面的分解形式：

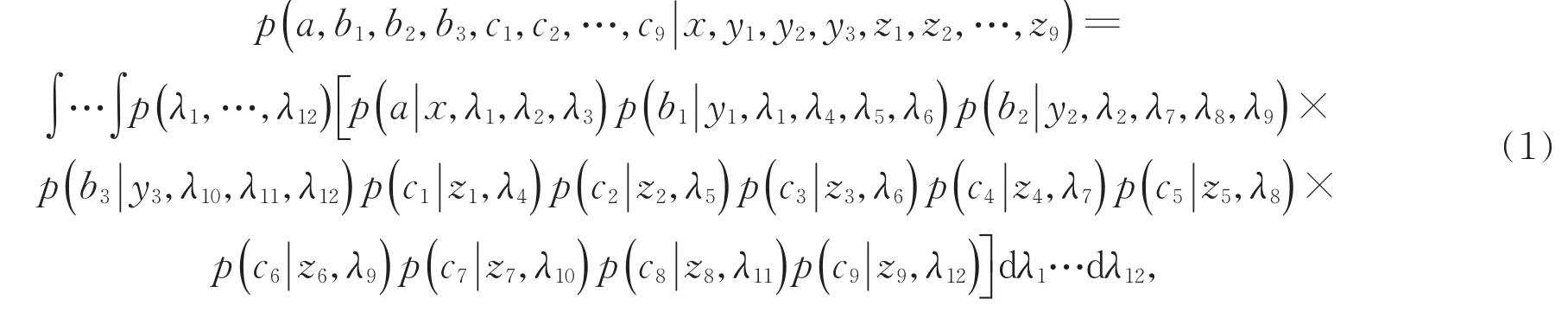
则称该树型量子网络所产生的关联是局域的。此外，若上述概率分布还满足概率条件

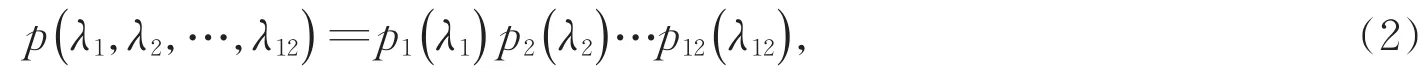
其中pi是λi的概率分布(i=1，2，…，12)，则称该网络产生的关联是12局域的；否则，则称为非12局域的。

接下来讨论图1所示树型量子网络的12局域不等式。下面是本节的主要结果。

定理1图1所示的树型量子网络若是12局域的，则其一定满足下面的不等式：

注1由定理1可知，只要图1所示树型量子网络所产生的关联是12局域的，那么就一定满足式（3）中的所有256个不等式。由此可知，只要违反了256个不等式中的至少一个不等式，即蕴涵该树型网络是非12局域的。此外，不等式（3）中的界是紧的。为此，考虑下面的方案：

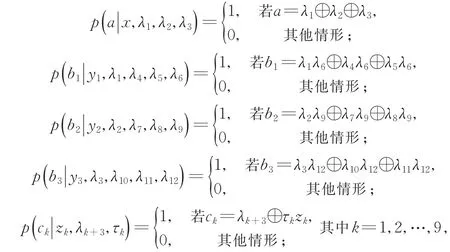
这里，λi是两个观测者之间共享的隐变量，服从分布pi(λi=0)=1(i=1，2，…，12)；τj是观测者Cj的局域随机资源，服从分布pj(τj=0)=r，pj(τj=1)=1-r，r∈ [0，1](j=1，2，…，9)。对于该关联，计算可得，对任意的i1，i2，i3，i4，j1，j2，j3，j4∈ {0，1}，均有Ii1，i2，i3，i4，0=r9且Ij1，j2，j3，j4，1=(1-r)9。进而得到对所有的i1，i2，i3，i4，j1，j2，j3，j4∈ {0，1}成立。

证明主要定理之前，需要一个引理。

对于其他各种组合(i1，…，i4，j1，…，j4)，类似可证得上面的不等式亦成立。

证毕。

2 12局域不等式的量子破坏

3 对于噪声的鲁棒性

4 结论

近十余年来，不同量子网络的非局域性研究受到许多学者的关注。本文主要研究了包含13个观测者和12个两体物理资源的树型量子网络的非局域性，得到了该网络的12局域不等式，并证明了所有的纯纠缠态均违反该12局域不等式。这里，我们只考虑了纯态的情形，对于混合态是否违反该12局域不等式，以及相应的结论能否推广到更一般的树型量子网络，有待于进一步研究。