带干扰线性系统的动态补偿

冯红银萍

（山西大学 数学科学学院，山西 太原 030006）

0 引言

1948年,美国数学家维纳(Norbert Wiener,1894—1964)发表了著名的《控制论——关于在动物和机器中控制和通讯的科学》[1],这标志着控制理论的诞生。19世纪40年代至60年代一般被认为是古典控制论时期,主要根据开环系统对某些信号的响应特征,用传递函数的办法来研究单输入、单输出时不变系统。现代控制理论时期大约在19世纪60年代至80年代,主要用状态空间法研究多输入、多输出系统。与古典控制理论不同,数学工具在现代控制理论中有了大量的应用,产生了各式各样的控制方法,例如:最优控制[2]、动态规划方法[3]、卡尔曼滤波理论[4]、自适应控制[5,6]、非线性控制[7,8]、鲁棒控制[9,10]以及变结构控制[11,12]等等。然而这些方法大多以数学模型为出发点,如果数学模型不能充分准确地描述实际系统,达到“工业逼近(Engineering Approximation)”[13]的要求,基于模型的控制将会是空中楼阁,其应用价值将大打折扣。因此,基于模型的控制方法必须考虑控制对系统的鲁棒性。现代控制理论的主要关注点之一就是系统的鲁棒性研究。19世纪80年代以来,涌现出各式各样的处理系统“不确定”的方法。例如:和本文密切相关的自抗扰控制(Active Disturbance Rejection Control)[14-16]和内模原理(Internal Model Principle)[17,18]等。

近年来,自抗扰控制越来越得到人们的关注,这源于其丰富而成功的实际应用案例[19-23]。自抗扰控制把外部干扰和未建模动态统称为干扰,并将其作为一个状态来进行估计。因此,相应观测器通常称为扩张状态观测器。自抗扰控制采用估计/消除策略，其核心是系统状态和干扰的在线估计。由于高增益的作用,当干扰满足某种有界性假设时,扩张状态观测器在理论上总是有效的。这说明扩张状态观测器对系统模型有很强鲁棒性。事实上,自抗扰控制几乎是一种不依赖于模型的控制[24]。然而任何事物都具有两面性,对系统模型的强鲁棒性既是自抗扰控制的优点也是它的缺点。人们往往关注优点却忽略了它的缺点:系统和干扰的先验信息利用不充分。内模原理中被充分利用的干扰动态信息在自抗扰控制中几乎没有得到任何利用。考虑标量系统˙x(t)=d(t)+u(t),其中x是状态,d是干扰,u是控制。如果我们已知d是频率为ω的正弦信号,那么“已知的频率ω”这一先验信息在传统的自抗扰控制中几乎没有得到有效利用。事实上,自抗扰控制仅仅利用了干扰导数˙d的有界性。从信息优化利用的角度看待控制问题,很容易发现自抗扰控制的这一缺点。实际应用中,人们往往并不是对被控对象一无所知,干扰或系统本身的周期性、光滑性、有界性以及一些“粗略的”动态信息也非常有助于控制设计。这些信息的浪费意味着控制性能还有提升的空间。与自抗扰控制类似,其他干扰处理方法也不同程度地存在着信息利用不充分的问题。例如：滑模控制、非线性控制、高增益控制等。

内模原理可以利用干扰的动态信息,总假设干扰动态信息已知,即:假设干扰来源于某个动态已知的外部系统。它在系统输出调节[18]问题中得到了有效的应用。内模原理在数学上堪称完美,但其控制设计严重依赖于数学模型,很难处理一般的干扰,对系统的鲁棒性也远不如自抗扰控制。内模原理的这一缺点恰好对应着自抗扰控制的优点,它们之间的优势互补促成了本文提出的线性系统动态补偿方法。如果将干扰的动态假设看作系统的先验信息,内模原理是干扰动态信息利用的有效手段之一,这一点恰好可以弥补自抗扰控制信息利用不充分的缺陷。

从信息提取和信息利用的角度来看,系统观测和控制的过程本质上是信息提取和信息利用的过程。跳出控制领域来看待自抗扰控制和内模原理,这两种方法的优点和缺陷是显而易见的。自抗扰控制借助于高增益充分利用了干扰的某种有界性信息,但对干扰的动态信息利用不足;而内模原理则侧重于利用外部干扰的动态信息,忽略了高增益对干扰的抑制作用。它们都在一定程度上存在着信息利用不充分的问题,因此还有改进的空间。在此认识的基础之上,本文提出线性系统的动态补偿方法。该方法包括动态信息提取和利用两个方面。篇幅所限,本文中的信息提取主要指干扰和系统状态的在线估计,信息利用主要指基于估计/消除策略的反馈设计。

线性系统的动态补偿方法可以充分利用系统和干扰的动态信息。当先验信息很少,只知道干扰的某种有界性时,新的控制策略恰好是自抗扰控制;当干扰先验动态信息完全已知时,新策略自动变为内模原理。也就是说,自抗扰控制和内模原理是线性系统动态补偿方法的两个极端情况。新方法更重要的价值在于它可以处理介于两种极端情况之间的,更符合实际情况的广泛情形。现有控制方法大多追求控制策略的广泛性,即:在尽可能少的假设下得到满意的控制效果。与此不同,线性系统动态补偿方法从已掌握的先验信息出发来设计控制策略,强调控制对系统的针对性而不追求广泛性,这是与现有方法完全不同的控制设计范式。

本文结构安排如下:第1节讨论控制模型的建立;第2节给出信号动态的定义,并讨论干扰系统可观性;高增益及其使用条件在第3节给出;第4节给出了扩张动态观测器的设计,并证明其适定性;干扰动态的选择在第5节讨论;观测器和控制器性能比较在第6节讨论,并给出闭环系统的数值模拟。在最后一节,第7节,我们对全文做了总结,并给出今后的研究工作。

1 控制模型

线性系统动态补偿方法并不局限于处理线性系统的问题,它还可以处理带有一般干扰的非线性控制问题。给定控制对象,按照对系统的认知情况,可将系统动态信息分为已知动态和未知动态两部分。已知动态主要指可以利用的线性动态结构,其余的都是未知动态,主要包括:未知的系统动态、已知动态结构和实际系统之间的误差、无法利用的复杂非线性动态以及外部干扰等。如果把未知动态都当作干扰,那么绝大多数实际控制系统都是可以模型化的。系统动态的分类将系统模型化建立在对控制系统先验认知的基础之上,先验信息越充分,系统模型就越准确。实际应用中,人们不可能对控制系统一无所知,系统及其干扰的有界性、光滑性、周期性以及一些粗略的动态信息都是系统建模和控制设计应该充分利用的素材。

动态补偿控制方法的核心在于干扰的处理。我们将优化组合内模原理和高增益方法来处理干扰。本文主要考虑如下系统:

其中A∈Rn×n是系统矩阵,用来表示已知的系统动态信息；是干扰,用来表示动态结构未知的部分；F∈Rn是控制向量；C∈R1×n是输出向量；u(t)是控制；y(t)是输出；B∈Rn表示干扰输入系统的方式。数学模型(1)可以看作被控对象的先验动态信息,它反映了人们对实际控制系统的认知。干扰d可以看作实际系统的未知动态,它反映了系统模型的准确性。特别地,当d=0时,系统完全已知。一般情况下,人们对干扰d并非一无所知,可能不同程度地掌握一些它的先验信息。与自抗扰控制和内模原理不同,我们将充分利用这些“粗略的”先验动态信息来提高控制性能。模型(1)涵盖的控制系统非常广泛。当

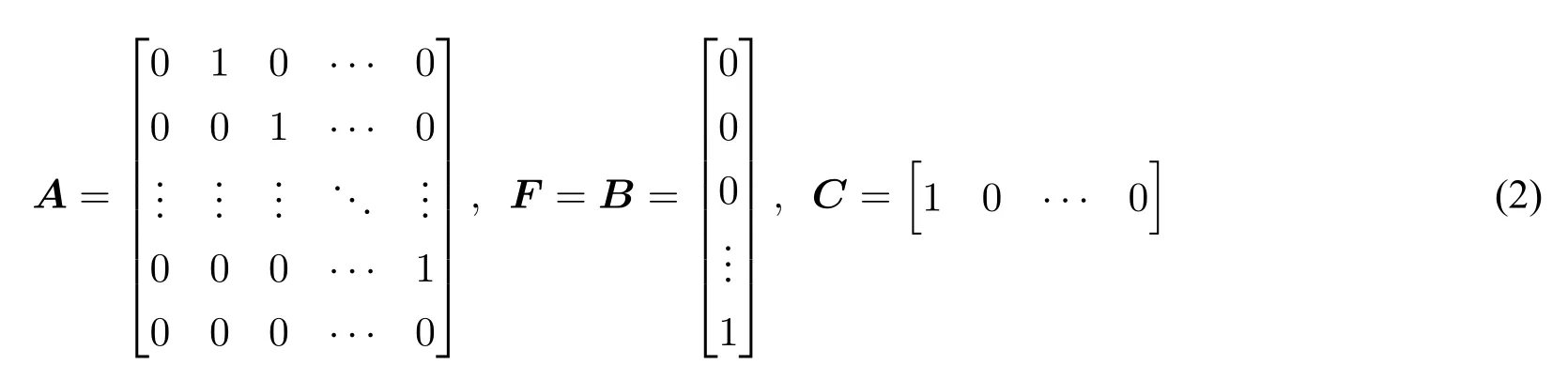
时,系统(1)正是自抗扰控制所研究的标准系统[14,25]。因此,基于模型(1)的控制策略对实际控制系统具有比自抗扰控制更强的鲁棒性。

如果已知干扰d(t)和系统状态x(t)的在线估计(t)和(t),那么系统(1)几乎是一个已知的线性系统,因而处理起来相对容易。特别地,如果B=F,控制器可以自然地设计为

如果不加特别说明,n,m和N在本文中总表示正整数。Rn表示n维欧式空间,其上的范数记为‖·‖Rn。矩阵A的特征值的全体记为σ(A),特征值实部最大值记为Λmax(A),矩阵A的转置为A⊤。简单起见,我们引入符号 C+={λ∈C|Reλ≥0},R+=(0,+∞)和‖·‖∞=‖·‖L∞[0,∞)。

2 信号的动态和干扰系统可观性

本节考虑干扰动态的定义,作为干扰的先验信息,它将被用于干扰估计。一般地,并不是所有的干扰信号都可以被一个确定的动态系统在线估计。例如:如果干扰恰好是某个Wiener过程的样本道路,它处处连续但处处不可微,因此不含有任何确定的动态信息。这样的信号很难用确定的动态系统来估计。据此,我们将干扰限制在如下Sobolev空间中:

其中Df是f的弱导数,定义为

由文献[26]中Theorem 5,W1,∞(R+)中的信号是几乎处处可微的,其所包含的信号非常广泛,常见的谐波信号、有界连续可微的周期信号、分段有界的多项式信号、指数信号、对数信号及其线性组合都在W1,∞(R+)中。此外,W1,∞(R+)还包含诸如

之类的按段连续的信号。

给定Rm中的单输出可观系统(G,Q),定义信号集合

由常微分方程理论,系统(G,Q)可观意味着

于是Ω(G)与Q无关,所以符号Ω(G)中没有出现Q也不会产生任何歧义。若干扰d∈Ω(G),则d的动态完全由G来决定。因此,我们可以用矩阵G来衡量d的动态信息。

任意给定矩阵G和函数s∈W1,∞(R+),记函数s在Ω(G)上的最佳逼近为PGs,即:

由于W1,∞(R+)是Banach空间,最佳逼近PGs∈Ω(G)总是存在的。

定义1若d∈Ω(G),则称G包含了信号d的动态。如果存在非零常数信号属于Ω(G),则称G包含了常数动态。

如果G包含了信号d的动态,则存在输出向量Q和初值v0使得d可以动态地表示为:

如果0∈σ(G),则对任意的常数信号c,有c∈Ω(G),于是G包含了常数动态。设dN是频率为ω1,ω2,···,ωN的谐波信号,即:

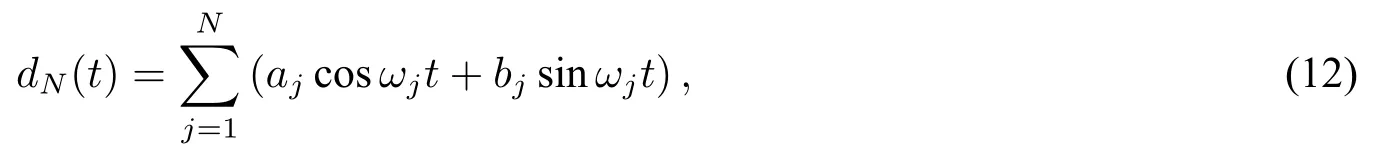
其中aj,bj∈R是振幅,j=1,2,···,N。由常微分方程理论,G包含dN的动态当且仅当σ(G)={±ωji|j=1,2,···,N}。当σ(G)⊂iR且G的每个特征值都是代数单的时,由 (8)可得 Ω(G)⊂W1,∞(R+)。特别地,当G=0 时,

则ηG(s)可以一定程度上度量G所包含s的动态。事实上,如果ηG(s)=0,则G完全包含s的动态;如果ηG(s)=1,则G不包含s的任何动态;0＜ηG(s)＜1表示G部分地包含s的动态。

定义2令A∈Rn×n,B∈Rn,C∈R1×n。假设Θ是信号集合并且已知d∈Θ。如果系统(1)的初值和干扰可以被输出辨识,即:对任意T＞0,有

则称系统(1)关于信号集合Θ可观。

引理1设系统(1)中的矩阵A,B,C具有如下观测标准型:

其中aj,bj∈R,j=1,2,···,n,则系统 (1)关于W1,∞(R+)可观当且仅当b2=b3= ···=bn=0 且b10。

证明设b10,b2=b3=···=bn=0,则对任意的T＞0,u(t)在[0,T]几乎处处为零意味着

其中x(t)=[x1(t)x2(t) ···xn(t)]⊤。若y(t)=xn(t)=0 a.e.t∈[0,T],由(17)可得

注意到b10,上式意味着d(t)=0 a.e.t∈[0,T]。所以,系统(1)关于W1,∞(R+)可观。

另一方面,假设系统(1)关于W1,∞(R+)可观。我们首先断言bn=0。否则,对任意T＞0,

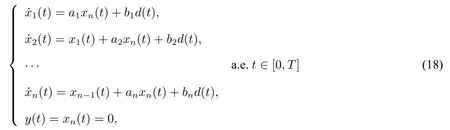
意味着xn-1(t)+bnd(t)=0 a.e.t∈[0,T]。所以,系统(18)变为

因为关于输出xn-1(·)的观测系统(19)恰好是观测标准型,所以对任意的bj∈R,j=1,2,···,n,该系统总是可观的,于是系统(19)满足xn-1(t)=-bnd(t)0 a.e.t∈[0,T]的任意非零解都是系统(18)的零动态。这与系统(1)的可观性矛盾。所以我们得到bn=0。与此类似,我们可以证明bn-1=0。事实上,对任意T＞0,由系统

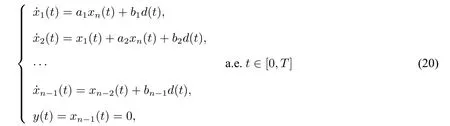
可得xn-2(t)+bn-1d(t)=0 a.e.t∈[0,T]。于是系统(20)变为

因为关于输出xn-2(·)的观测系统(21)恰好是观测标准型,对任意的bj∈R,j=1,2,···,n-1,该系统总是可观的,于是系统(21)满足xn-2(t)=-bn-1d(t)0 a.e.t∈[0,T]的任意非零解都是系统(18)的零动态。这与系统(1)的可观性矛盾。所以我们得到bn=bn-1=0。重复上述步骤,我们最终得到bn=bn-1= ···=b2=0。注意到B0,定理得证。

由引理1,当系统(1)关于W1,∞(R+)可观且B=F时,系统(1)的观测标准型(16)满足

这正是自抗扰控制中的常见形式。

引理2设A∈Rn×n,G∈Rm×m且

则系统(1)关于Ω(G)可观当且仅当(A,C)可观且如下传输零点条件成立:

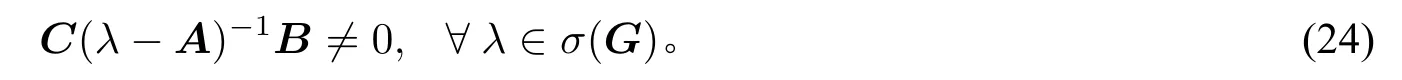
证明因为已知d∈Ω(G),所以存在Q∈R1×m使得系统(G,Q)可观并且干扰可以动态表示为:

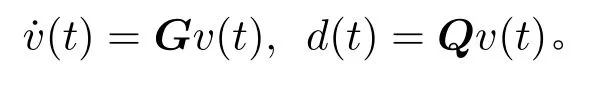
于是当u(t)=0时,系统(1)可以表示为:

如果定义

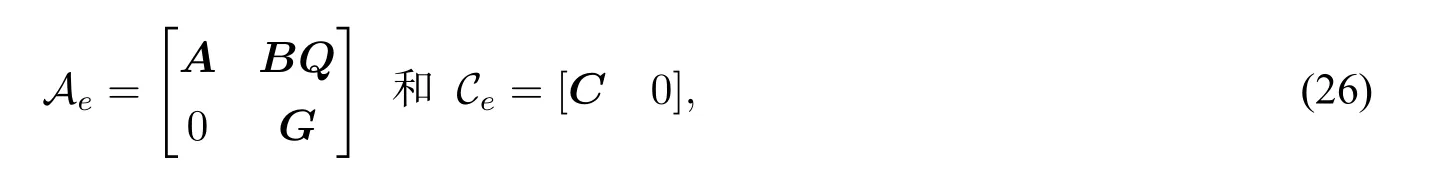
则系统(1)关于Ω(G)可观当且仅当系统(Ae,Ce)可观。

设系统(Ae,Ce)可观且存在τ＞0使得CeAtx≡0,∀t∈[0,τ]。那么CeeAet(x,0)⊤=CeAtx≡0意味着x=0从而系统 (A,C)可观。对任意的λ∈σ(G)⊂σ(Ae),设Ae(x,v)⊤=λ(x,v)⊤,其中(x,v)⊤0。由文献[27]Remark 1.5.2和系统(Ae,Ce)的可观性可知,

于是(24)成立。

另一方面,对任意的λ∈σ(G)⊂σ(Ae),设Ae(x,v)⊤=λ(x,v)⊤且Ce(x,v)⊤=0,则有C(λ-A)-1BQv=0且Gv=λv。由假设(24)可知Qv=0,从而利用系统(G,Q)的可观性可得v=0。所以,方程组Ae(x,v)⊤=λ(x,v)⊤,Ce(x,v)⊤=0简化为Ax=λx,Cx=0。由系统(A,C)的可观性,x=0。因此,系统(Ae,Ce)可观,或者等价地,系统(1)关于Ω(G)可观。

干扰系统(1)的可观性与干扰集合Θ密切相关。这里Θ相当于干扰的先验信息。相同的系统在不同的先验信息下的可观性可能不同。下面举例说明这一情况。令

则当u=0时,系统(1)可以写成

假设我们仅知道d∈W1,∞(R+)。简单计算可知x1(t)=x2(t)=d(t)=sT(t)是系统(29)在[0,T]上的一个非零解,其中sT由(7)给出。然而显然有d∈W1,∞(R+)并且y(t)=x1(t)-x2(t)≡0,t∈[0,T]。由定义2,系统(29)关于W1,∞(R+)是不可观的。

当我们已知干扰d的动态,即存在矩阵G使得d∈Ω(G)且0,1/∈σ(G)时,情况会变得完全不同。事实上,存在向量Q使得系统(G,Q)可观,并且系统(29)可以写成

由引理2,系统(30)可观,于是系统(1)关于Ω(G)可观。这与关于W1,∞(R+)的可观性完全不同。这一事实表明:干扰的先验信息对干扰系统的可观性有很大的影响。先验信息越充分,对系统的认知就越多,从而越有助于我们观测系统。所以,只要干扰先验信息足够充分,即使系统(1)关于W1,∞(R+)不可观,我们仍然可能利用系统(1)的输出估计出干扰d。

注记1 对于无干扰系统,它在某个区间[0,T]上可观等价于在整个区间[0,+∞)上可观。这与干扰系统的可观性大不一样。由于干扰的不确定性,利用输出信号在[0,T]上的信息来估计干扰在[T,+∞)上的值几乎是不可能的。因此,干扰系统可观性定义2是合理的。

3 高增益及其使用条件

在很多情况下,我们不得不为干扰的抑制付出代价,这种代价在一定程度上可以用高增益来衡量。控制器增益越大,其处理干扰的能力就越强。由于不需要太多的干扰先验信息,高增益在控制器和观测器的设计中得到广泛的应用,PID控制对系统的强鲁棒性也离不开高增益的身影。尽管高增益这个名词在控制领域并不陌生,但是究竟什么是高增益却缺乏严格的数学定义,不同知识背景的研究人员可能对高增益有不同的理解。现在我们从数学的角度探讨高增益及其工作机理。

简单起见,考虑如下带有干扰的标量系统:

其中d∈L∞[0,∞)是干扰,ω＞0是调节参数。解系统(31)得:

这意味着x可以通过增加反馈增益ω来任意镇定。也就是说,可以通过增加反馈增益ω来减轻干扰d对系统(31)的负面影响。对于一般的系统

其中Aω∈Rn×n是Hurwitz矩阵,-ω=Λmax(Aω),B∈Rn。如果存在不依赖于ω和t的常数LB＞0使得

则系统(34)的解满足

因此,如果条件(35)成立,系统(34)就可以通过调节增益ω来镇定。然而(35)并不是对所有的可控系统(Aω,B)都成立。例如:若

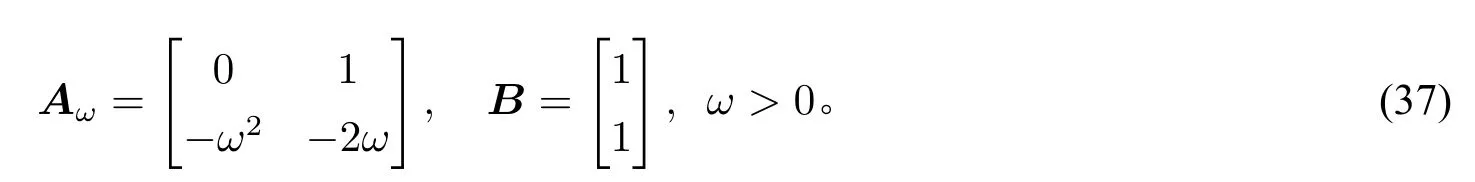
容易验证系统(Aω,B)是可控的,但(35)不成立。事实上,直接计算可知

特别地

上述例子说明,并不是所有的控制系统都可以用高增益来抑制干扰。下面给出一个高增益起作用的充分条件。

引理3设Aω∈Rn×n是Hurwitz矩阵,ω＞0是矩阵Aω特征值实部最大值的相反数,即:-ω=Λmax(Aω)。若向量B∈Rn满足

则存在不依赖于ω和t的常数LB＞0使得(35)成立。从而对任意的d∈L∞[0,∞),系统(34)的解满足

证明令εj=[0 ···0 1jth0 ···0]⊤,其中 1jth表示第j个坐标分量为 1,j=1,2,···,n。由假设(40)知:

利用Laplace反变换可得:

其中γ是实数使得积分收敛,j=1,2,···,n。由于矩阵Aω是Hurwitz矩阵,(43)意味着(35)成立。注意到

所以(41)成立。

4 扩张动态观测器

给定d∈W1,∞(R+),设ηG(d)是d在Ω(G)上最佳逼近的相对误差,由(14)定义。当ηG(d)=0时,内模原理可以补偿干扰d的负面影响;当ηG(d)=1时,我们可以借助于高增益来压制干扰。然而实际应用中最常见的情况是:0＜ηG(d)＜1的情况。此时如何充分利用这一没有完全确定的先验信息呢？本节通过设计扩张动态观测器来回答这一问题。受内模原理启发,我们首先将干扰d写成动态形式。

引理4令系统(G,Q)是Rm+1上可观的单输出系统,设0∈σ(G),则对任意的d∈W1,∞(R+),存在v0∈Rm+1使得

其中Bd∈Rm+1是矩阵G的属于特征值0的特征向量,e=(I-PG)d,PG由(10)给出。

证明由假设和Hautus引理（见文献[27]15页Remark 1.5.2）可得KerG∩KerQ={0}。注意到GBd=0和Bd0,所以QBd0,从而系统(44)中第一个方程的分母有意义。

由于PGd∈Ω(G),存在某些初值,使得

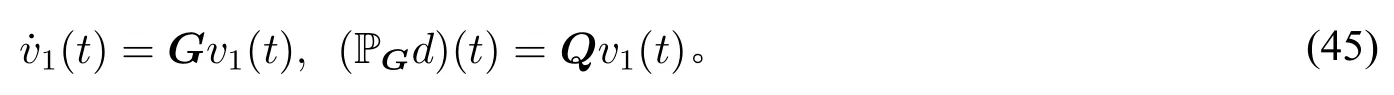
注意到GBd=0,如果我们令

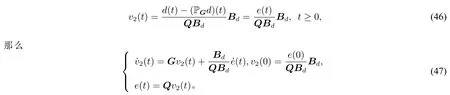
若令v(t)=v1(t)+v2(t),综合系统(45)和(47)可得系统(44)。

由于d∈W1,∞(R+),d几乎处处可微（见文献[26]280页Theorem 5）,于是误差e也是几乎处处可微的。因此(44)中的˙e有意义。有了上述准备工作,现在可以为系统(1)设计观测器了。注意到任意可观系统(A,B,C)都可以写成观测标准型(16),由引理1,不失一般性,我们总假设A,B,C,G和Bd满足:

假设1令n和m是正整数,矩阵或向量A,B和C由(16)给出,其中b1=1,b2=b3=···=bn=0。设G∈R(m+1)×(m+1)和E,Bd∈Rm+1为

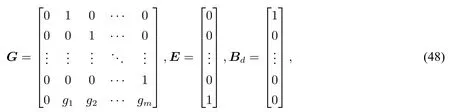
其中gj∈R,j=1,2,···,m使得

假设(48)意味着0∈σ(G),即:G包含常数动态,且对任意的gj∈R,j=1,2,···,m,总有GBd=0。满足(49)的矩阵G包含大多数常见信号的动态,例如:谐波信号、多项式信号、指数信号以及它们的有限线性组合。

受文献[28]的启发,系统(1)的观测器设计如下:

其中观测器参数矩阵G,E,Kωo,S和Q按照如下步骤选择:

·根据假设1和干扰的先验信息确定G和E(详细内容将在第5节讨论);

·选择K=[k1-a1k2-a2···kn-an]⊤和P=[p0p1-g1···pm-gm]使得矩阵A+KC和G+EP是Hurwitz矩阵。令

其中ωo＞0是调节参数;

·解方程组

得到S∈Rn×(m+1)和Q∈R1×(m+1)。

和原系统(1)相比,观测器(50)扩张了动态G,因此称为扩张动态观测器。扩张动态选定之后，影响观测器性能的调节参数主要是ωo。所以,扩张动态观测器是便于实际应用的。为了证明观测器(50)的适定性,我们首先给出如下引理:

引理5在假设1下,观测器参数矩阵G,E,Kωo,S和Q满足:

(i)方程组(53)总是可解的;

(ii)系统(G,Q)可观;

(iii)对任意的s∈C+,存在不依赖ωo,s的正常数CK和CA,使得

(iv)对任意的s∈C+,存在不依赖ωo,s的正常数CG,使得

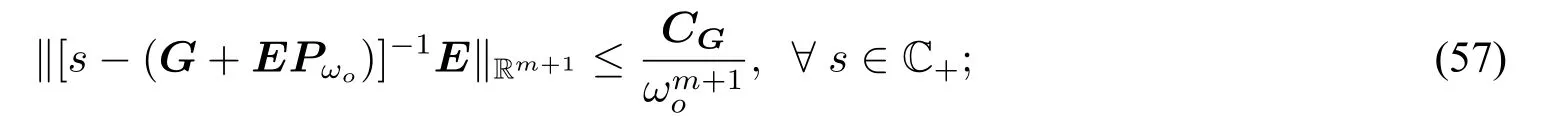
(v)如果G可对角化,存在不依赖ωo,s的正常数CS和CQ,使得

证明(i)由于A+KC是Hurwitz矩阵和我们对A,B,C以及Kωo的恰当选择,简单计算可知A+KωoC也是Hurwitz矩阵,并且

注意到

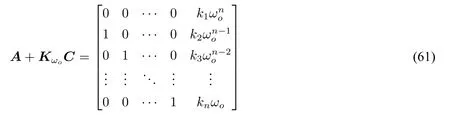
是Hurwitz矩阵,(49)意味着

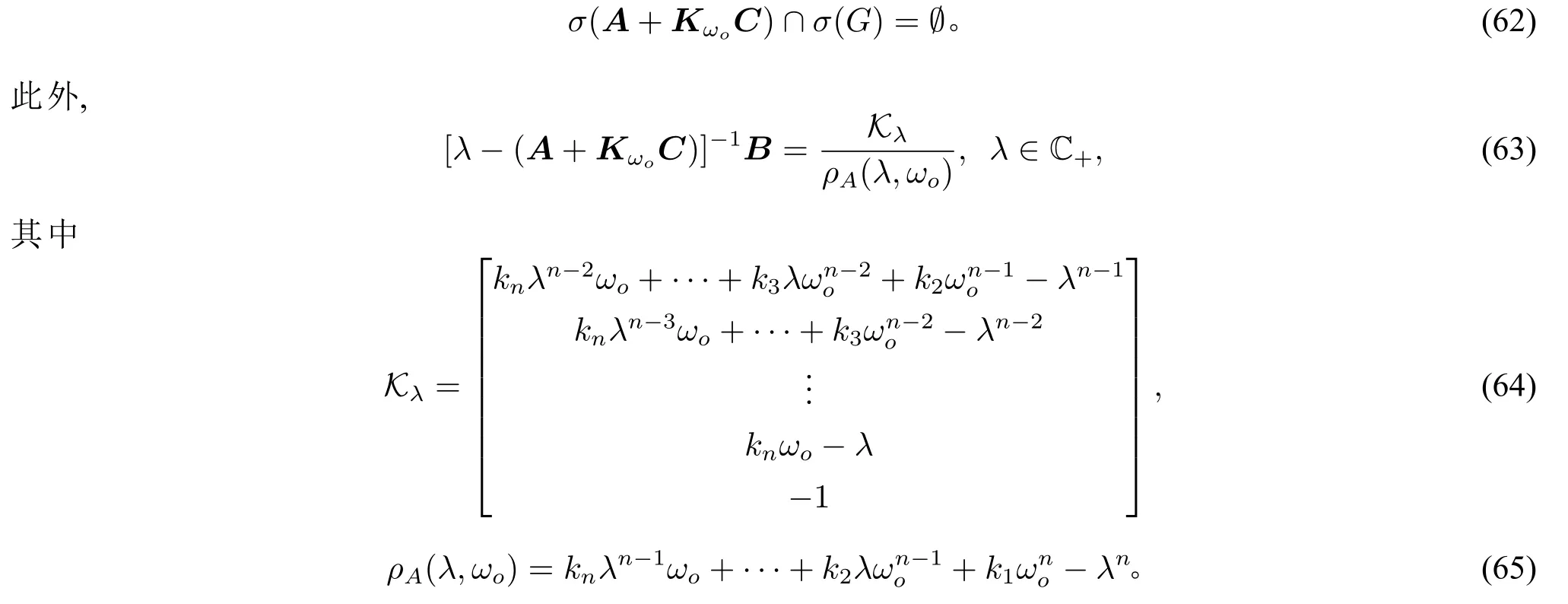
于是,下面传输零点条件成立:

由文献[29],式(62)和(66),方程组(53)可解。

(ii)设Gh=λh且Qh=0,其中λ∈σ(G),则方程组(53)中的Sylvester方程变为(A+KωoC-λ)Sh=BQh=0。由(62)可得λσ(A+KωoC),从而A+KωoC-λ是可逆的。所以,Sh=0且CSh=Pωoh=0。由文献 [27]Remark 1.5.2,当系统 (G,Pωo)可观时,有h=0。再次利用文献[27]Remark 1.5.2,系统(G,Q)也是可观的。综上,只需证明系统(G,Pωo)可观即可。事实上,对任意的Gv=λv和Pωov=0,其中λ∈σ(G),我们有(G+EPωo)v=Gv=λv。由于G+EP是Hurwitz矩阵,综合(48)和(52)可得矩阵G+EPωo也是Hurwitz矩阵,并且有

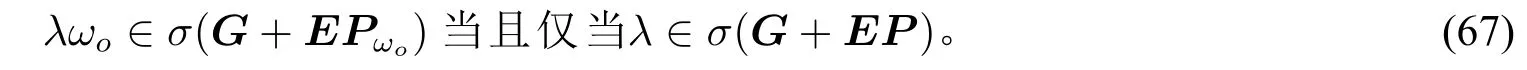
由(49)和λ∈σ(G),有λ/∈σ(G+EPωo)。因此,(G+EPωo)v=λv意味着v=0。利用文献[27]Remark 1.5.2,系统(G,Pωo)可观。

(iii)由于A+KωoC是Hurwitz矩阵,(61)意味着k10。因此(54)可以综合(63),(64)和(65)得到。注意到GBd=0,由(53)可得

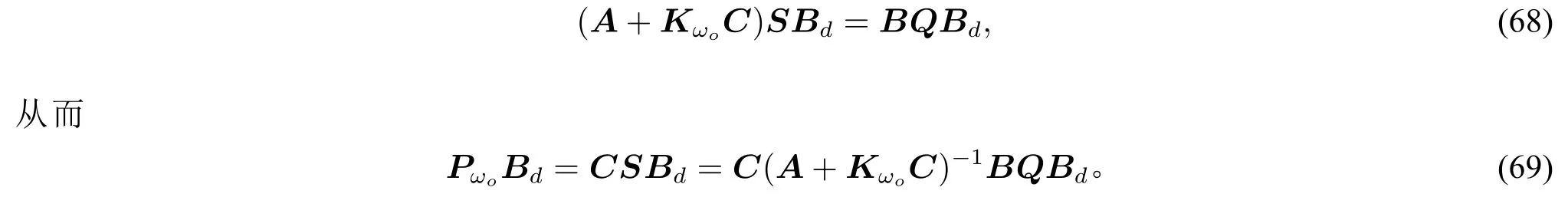
由 (48)和 (52)得

注意到系统(G,Q)可观并且GBd=0,由Hautus引理[27,p.15,Remark1.5.2]可得QBd0。于是,综合(66),(70)和 (69)可得并且

从而(55)成立。注意到(61),对任意的s∈C+,直接计算可得

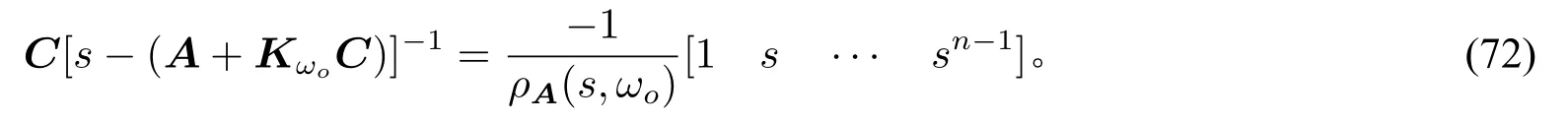
综合(72)和(65)容易推出(56)。

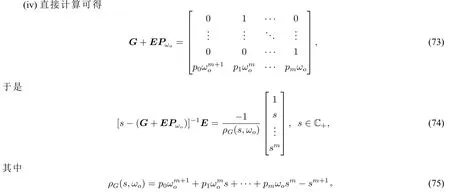
因为G+EPωo是Hurwitz矩阵,所以有p00,从而综合(74)和(75)可推出(57)。

(v)由于矩阵G可对角化,对任意的v∈Rm+1,存在序列v0,v1,···,vm使得

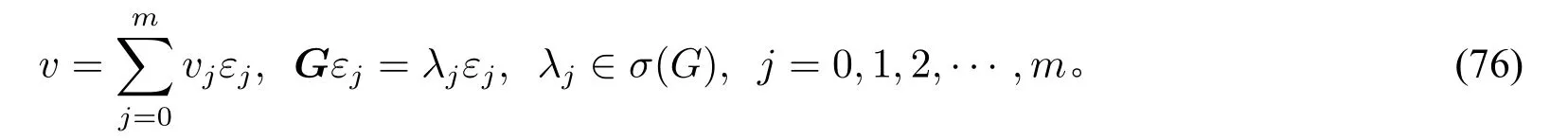
由(53),(63)和(66)可得:

该式结合(76)和(77)可推出

综合(64),(52)和(80),我们容易得到(58)。

注意到(75),(73)和(48),对任意的s∈C+,直接计算可得

由于p00,存在不依赖ωo和s的正常数M1使得

所以,由(58),(56)和(82)可得

综合(52),(75)和(81),存在不依赖ωo和s的正常数M2,使得

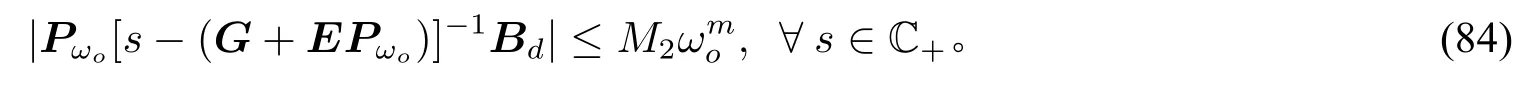
对任意的v∈Rm+1,由(53)和(66)可得

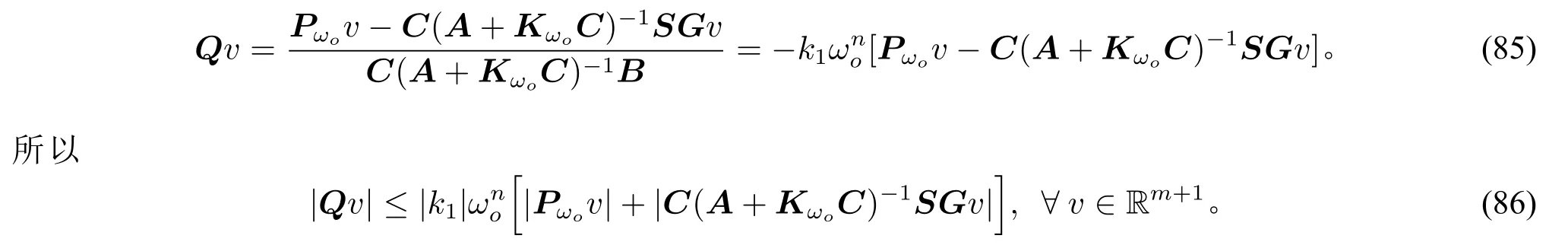
综合该式和(83),(84),可以推出(59)。

定理1设假设1成立,并且矩阵G可对角化,则系统(1)的扩张动态观测器(50)是适定的,即:对任意的干扰d∈W1,∞(R+)和初值((0),(0))∈Rn×Rm+1以及任意的控制存在不依赖ωo的正常数M1使得

其中e=(I-PG)d,PG由(10)给出。特别地,存在不依赖ωo的正常数M2使得

该式结合(6),(89)和(44)可推出(88)。

注记2方程组(53)在鲁棒输出调节理论中被称为调节方程组[18]。当满足传输零点条件(24)时,该方程组总是可解的[18,Assumption1.4,p.9]。由引理2,只要系统(1)关于Ω(G)可观,调节方程组(53)总是可解的。在输出调节理论中,调节问题可解的充要条件是调节方程组可解[18]。这一结果说明:系统(1)观测器的设计和相应的输出调节理论之间存在着密切的关系。

注记3设ηG(d)是d∈W1,∞(R+)在Ω(G)上最佳逼近的相对误差,则由(14)和(87)可得

所以,观测器稳态误差估计依赖于d在Ω(G)上最佳逼近的相对误差ηG(d)和观测器的收敛速度-Λmax(A)=ωo。我们需要选择G使得ηG(d)尽可能地小。显然,G的选择依赖于人们对干扰的先验认知。干扰先验信息越多,误差ηG(d)就越小。特别地,当干扰d的所有动态都已知,即:已知G使得d∈Ω(G)时,有ηG(d)=0,从而观测器(50)的稳态误差将变为零。此时,观测器(50)变为完全基于内模原理的观测器。提高观测器精度的另一个方法是增加增益常数ωo。这正是高增益观测器的干扰处理方法。然而,在实际应用中,ωo不可能任意增大。因此单独通过增加ωo来提高观测器精度是不可行的。给出新的提高观测器精度的方法是本文的贡献之一。

注记4当ηG(d)=0时,干扰动态完全已知。此时误差系统(90)的系统矩阵相似于(94)中的矩阵AS。由于矩阵AS的对角结构,我们可以通过调节Kωo和Pωo使得系统(90)的极点任意配置。这就意味着控制系统和干扰的动态信息得到了充分的利用。

5 干扰动态选择

本节我们着重考虑扩张动态G的选取。由注记3,G的选取依赖于人们对干扰d动态信息的掌握。首先考虑最坏的情况:我们只知道d∈W1,∞(R+)。简单起见并不失一般性,假设系统(1)中的矩阵满足:

其中aj∈R,j=1,2。从观测器瞬态响应的角度来看,我们需要扩张动态G的阶数尽可能地小。注意到G=0包含常数动态,因此,在没有其他先验动态信息的前提下,我们选G=0来利用干扰信息“d∈W1,∞(R+)”。根据观测器(50)的参数选择策略,此时有

其中α3＜0,并且α1,α2∈R使得如下矩阵是Hurwitz矩阵:

解调节方程组(53)得

注意到(50)和(114),系统(1)的观测器设计如下

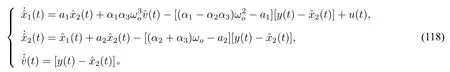
当A中a1=a2=0时,(118)正是自抗扰控制中的扩张状态观测器[25]或高增益观测器[30](相差一个可逆线性变换)。与文献[25,30]中观测器相比,观测器(118)更充分地利用了系统的动态信息(a1和a2的信息)。

在大多数的工业应用中,干扰的动态信息一般不会完全未知。在观测器设计之前,人们总会或多或少的掌握一些干扰动态信息。这些信息虽然不一定完全准确,但是对提高观测器性能非常重要。当干扰动态信息完全已知时,由注记3,可以选择G使得相对误差ηG(d)=0;当干扰动态信息部分已知时,我们应选择G使得ηG(d)尽可能地小。虽然扩大G的阶数可以减小相对误差,然而由于高增益的存在,动态G阶数的增大将给系统瞬态响应带来负面影响,可能产生“超调”“峰值”现象。因此从瞬态响应的角度来看,G的阶数不能任意扩大。

假设已知d∈W1,∞(R+)是一个连续可微的周期信号,并且大致知道该信号包含频率ωj,j=1,2,···,N。此时,干扰可以分解为两个部分d(t)=d1(t)+d2(t),这里d1∈W1,∞(R+)的动态未知,而d2的动态已知,即:

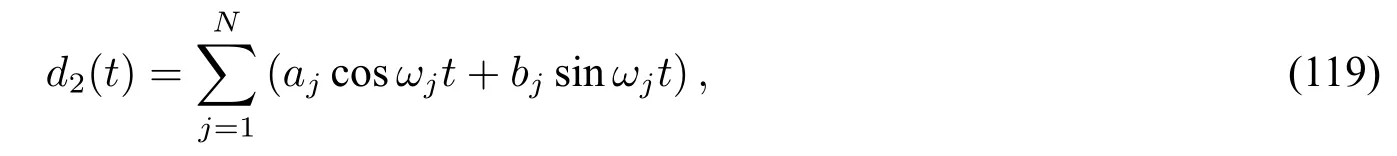
其中aj,bj∈R,j=1,2,···,N是未知振幅。利用已知的先验频率,我们选择g1,g2,···,g2N使得(48)中的矩阵G满足σ(G)={0,±ωji|j=1,2,···,N},m=2N。这里要求0∈σ(G)是为了消除常数干扰导致的观测器的静态误差。由Vieta定理,参数g1,g2,···,g2N的选择是容易完成的。注意到d2∈Ω(G),由定理1,d2的负面作用完全被补偿,因此观测器(50)的稳态误差上界此时正比于

众所周知,自抗扰控制中的观测器误差上界一般正比于‖‖∞[25,30]。如果干扰的频率ωj很大,那么‖‖∞也会很大。于是自抗扰控制方法很难处理这样的干扰,因为观测器增益不可能任意大。然而,扩张动态观测器却可以很好地工作,因为高频干扰被扩张动态完全补偿了。

假设d∈W1,∞(R+)是周期信号,且其周期T已知。由Fourier展开,

其中aj是Fourier系数,j=0,1,···。由于˙d∈L∞[0,∞),

注记5当矩阵G不可对角化时,矩阵的广义特征向量构成Rm+1中的一组基。此时定理1的结论也是成立的。当然,定理证明也要做相应的修正。如果在(48)中选择g1=···=gm=0,那么

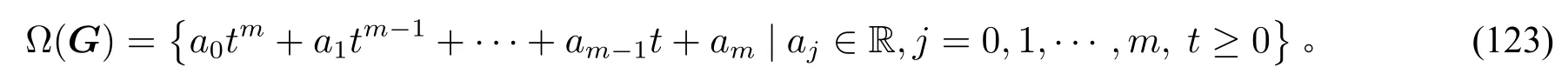
因此,观测器(50)对多项式信号或分段多项式信号仍然有效。不仅如此,观测器(50)还可以处理指数信号,例如:如果G满足σ(G)={0,λ},λ＞0,且λ的代数重数为nλ,信号tnλeλt属于 Ω(G)。

6 观测器和控制器的性能比较

控制策略的优劣是相对于具体控制问题而言的,实际需求和客观条件不同,控制策略的优劣评价结果也可能不同,控制性能并不是唯一的评价指标。控制方法的“好”和“坏”有一定的主观性,控制需求是判定控制方法“好”和“坏”主要依据,最能满足要求的就是最“好”的,尽管它可能在性能上不是最优。作为理论研究,本文只关注控制方法的控制性能。与自抗扰控制和内模原理相比,本文所提出的线性系统动态补偿方法在控制性能上有很大的优势。控制方法的性能比较的前提是:对系统有相同的先验认知。控制性能的科学比较是一个非常复杂的问题,简单枚举一个或多个控制算例并不足以说明控制方法在性能上的优劣。线性系统动态补偿方法的优势体现在对系统动态信息的利用上。

简单起见且不失一般性,本节通过一个简单例子来说明扩张动态观测器优势。令

考虑二阶观测系统:

其中α,β∈R是振幅,ω＞0是频率,d0∈W1,∞(R+)。假设我们已经知道的先验信息是:

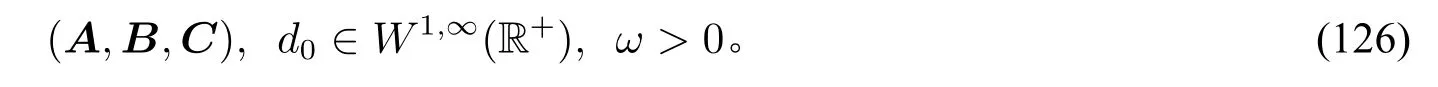
除上述信息外,其他信息全部未知。根据已知的先验信息,我们选择

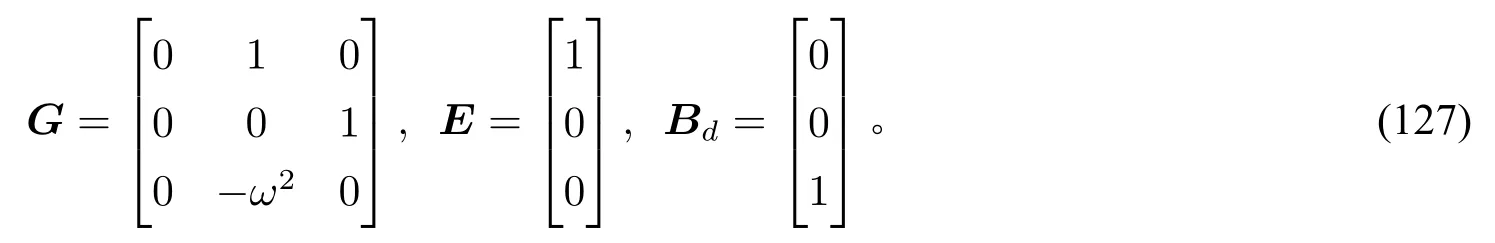
按照给定步骤,可得扩张动态观测器(50)。直接计算可知,逼近误差满足‖(I-PG)d‖≤‖d0‖W1,∞(R+)。记扩张动态观测器的稳态误差为e1,则由定理1,存在常数M1＞0使得

其中ωo是观测器增益。显然,先验信息(126)在扩张动态观测器(50)中得到了利用。而自抗扰控制中的扩张状态观测器浪费了先验频率信息ω。此外,系统矩阵A也不能信息完整地等价变换成自抗扰控制的标准形式[14,30]。记自抗扰控制中扩张状态观测器的稳态误差为e2,则存在常数M2＞0使得

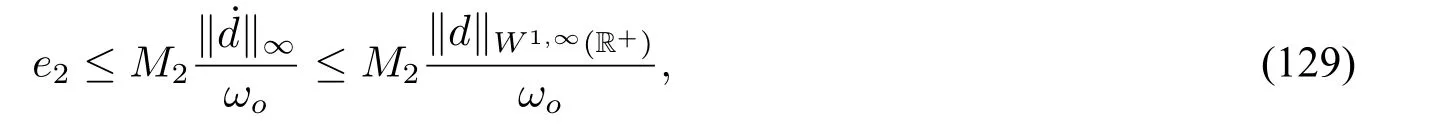
其中ωo是观测器增益。当ω很大时,‖d0‖W1,∞(R+)远小于‖d‖W1,∞(R+)。此时,在相同增益下,e1将远小于e2。上述分析可以看出,由于先验频率信息ω得到了充分的利用,当ω很大时,扩张动态观测器(50)比自抗扰控制更具有优势。此外,由于d0的一般性,内模原理无法处理(125)中的干扰类型。

现在考虑动态信息利用的问题:控制器设计。篇幅所限,本文只考虑干扰和控制在一个通道的系统镇定问题。注意到(124),系统(1)可以写成

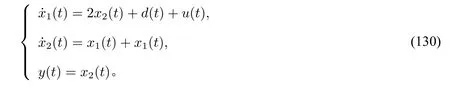
为了便于数值仿真,我们选取d(t)=sinωt+2,ω=10,x1(0)=0和x2(0)=1。如果观测器能够在线估计出系统状态和干扰,控制器可以由估计/消除策略(3)来设计:

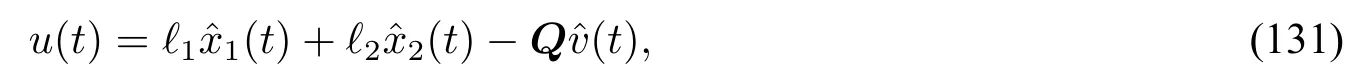
按照干扰d的先验动态信息,我们分三种情况分析控制器(131)的性能。情况一,‖d‖W1,∞(R+)已知;情况二,‖d‖W1,∞(R+)已知,且知道ω的一个估计=0.9;情况三,‖d‖W1,∞(R+)和ω都已知。针对这三种情况,我们对闭环系统(131)，(130)，(50)进行数值模拟,扩张动态系统的初值都为零,其他参数和相应的仿真结果参见表1。

表1 控制器的性能比较Table 1 Comparison of the controller

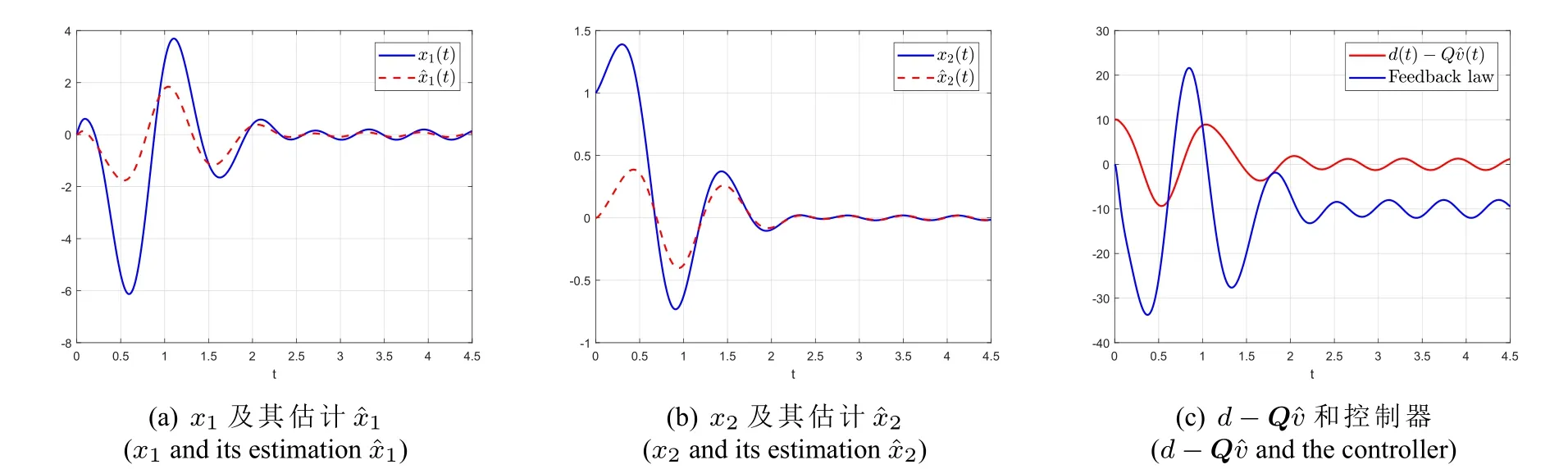
图1 情况一的仿真Fig.1 Simulation for case 1

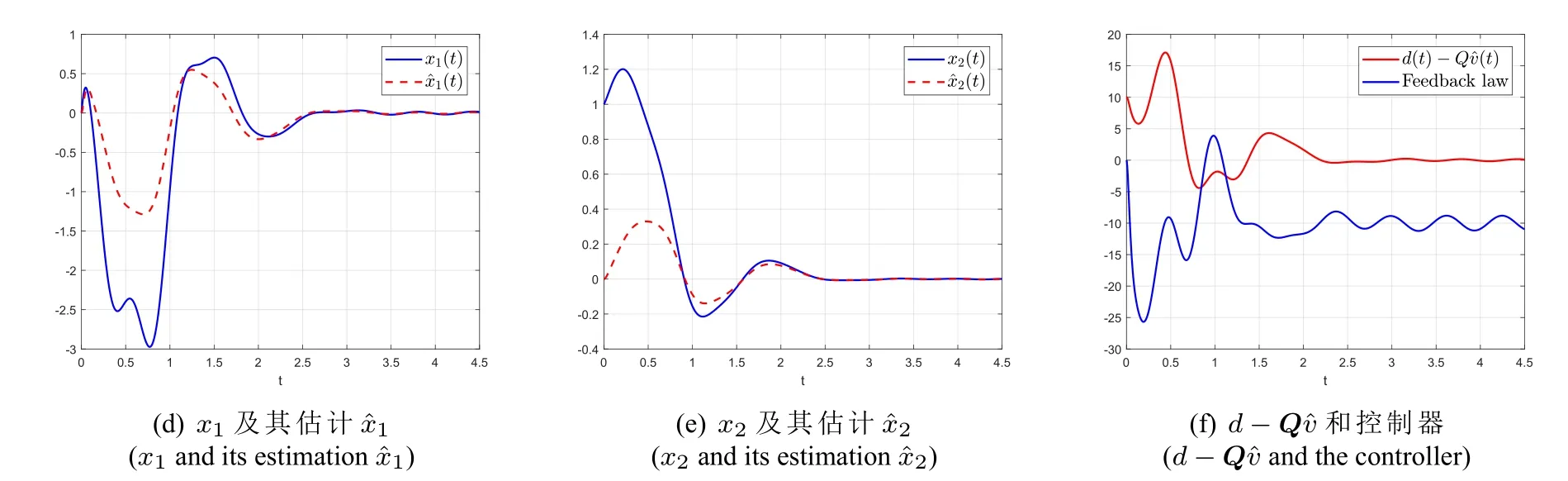
图2 情况二的仿真Fig.2 Simulation for case 2

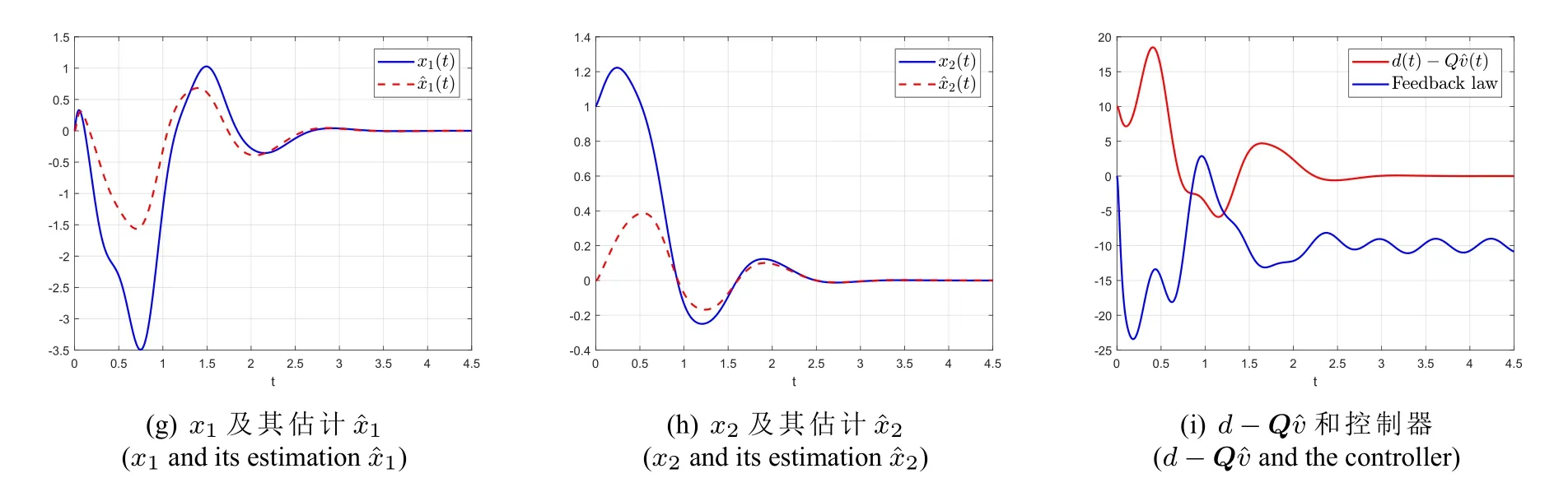
图3 情况三的仿真Fig.3 Simulation for case 3

从数值仿真可以看出,观测器精度随着干扰先验信息的增多而提高。当干扰动态信息完全已知时,观测器稳态误差为零。当先验信息很少时(情况一),动态反馈理论本质上就是自抗扰控制。情况二充分利用了干扰的先验动态信息,尽管观测器增益ωo并不是很大,观测器仍然得到很高的精度。当ω很大时,动态反馈方法的优势将变得特别明显。如果在情况二的先验假设下采用自抗扰控制策略将造成频率信息“≈ω”的浪费。

为了观察控制对测量噪声的敏感性,我们在系统(130)的输出中加入了白噪声,即:y(t)=x2(t)+1%ξ(t),其中ξ(t)是matlab中“randn”函数生成的白噪声。仿真结果见图4。可以看出控制器对测量输出中的白噪声不敏感,测量噪声对系统状态和观测器估计产生的影响很小。此外,必须要指出的是,观测器初始时刻会产生“峰值现象”,这和观测器的增益和扩张动态G的阶数有关。实际应用中有很多技术手段来处理“峰值现象”。本文在所有的仿真中对测量信号加入了简单的过渡过程来减轻观测器的“峰值现象”,即:输入观测器的信号为y(t)=(1-e-t)x2(t)。

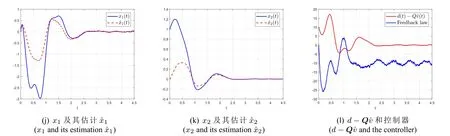
图4 情况二中测量加入白噪声Fig.4 Simulation for case 2 with white noise

7 结论

本文提出线性系统的动态补偿方法，用来处理带干扰的线性、非线性系统的控制问题。与传统控制方法不同，线性系统的动态补偿方法以系统和干扰的先验动态信息为出发点，将观测器设计和控制器设计看作动态信息的提取和利用。如果将未知动态和难以处理的复杂动态统称为干扰，大多数实际系统都可以通过带干扰的线性系统来模型化。我们给出扩张动态观测器来在线估计系统状态和干扰。新观测器强调对实际系统的针对性，不追求其广泛性，是与现有方法完全不同的观测器设计范式。自抗扰控制中的扩张状态观测器和基于内模原理的观测器是扩张动态观测器的两个极端情况。扩张动态观测器更重要的价值在于它可以处理介于这两种极端情况之间的，更符合实际情况的广泛情形。由于一些“粗略的”先验动态信息得以充分利用，观测器稳态性能得到了有效的提高。新方法是基于先验信息的控制设计策略，对控制系统有强鲁棒性。

系统和干扰的动态信息除了源于人们对它们的先验认知之外,还可能隐含在系统的测量输出中。因此,利用测量输出估计系统和干扰的动态信息可以使得控制设计在一定程度上摆脱人们对系统认知的依赖,使得控制器能够自动地适应被控对象。例如：如果我们能够利用测量输出估计干扰动态G,那么观测器(50)将摆脱对干扰动态先验认知的依赖。前期研究表明：系统和干扰的动态信息的在线估计需要最优控制的数学工具,这正是我们今后的研究内容。