一种考虑先验信息可靠性的新算法
赵 哲,柳翠明
(广州市城市规划勘测设计研究院,广东 广州 510000)
Bayes估计在参数估计过程中充分利用了未知参数的先验信息[1-2],但仍有以下局限:其一,需要获知参数的验前分布,但测量学中的先验信息来源多样且复杂,导致先验信息大多充斥着不确定性。这种不确定性既包含数值误差,也包含概念误差,既包含可度量误差,也包含不可度量误差[3-5]。导致许多先验信息没有统计性质,也不是一个具体数值,只能用参数的可行空间,噪声范围等来描述[6-7];其二,先验信息的可靠性直接影响着估计结果,可靠的先验信息可以提高估计效率,不可靠的先验信息反而会降低估计精度[8-10]。目前常采用相容性检验方法对先验信息进行取舍[11],认为先验信息完全可信或完全不可信,这一作法一定程度上提高了先验信息利用的科学性。但在测量学中,先验信息是指提前获取的信息,具有一定可信度,其可信度必不会单纯为0或1,而是分布于该闭区间[0,1]内。为此,许多专家提出了先验信息可靠性的度量方法并给出了可信度的计算公式[12-16]。但这些方法都是建立在概率论的基础上,对于大地测量学中广泛存在的充满不确定性的先验信息无能为力。针对以上问题,本文引入模糊理论,用模糊数集来描述测量学中的先验信息,依据小概率事件原理[17]构造参考信息,用先验信息与参考信息的模糊贴近度来衡量先验信息的可靠性,将其以权阵的形式纳入估计过程以平衡不同可靠度的先验信息在参数估计中的作用。适用于测量学中不确定性信息的数值化及其可靠性评估等问题。
1 模糊数与贴近度



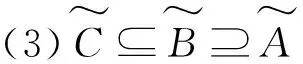
文献[18]给出了对称模糊数的贴近度公式:
(1)
2 可靠性的度量
本文通过构造一种近似完全可靠信息作为参考信息,用先验信息与参考信息的模糊贴近度来衡量先验信息的可靠性。
2.1 构造参考信息
由于完全可靠信息难以获取,文献[19]基于小概率事件原理构造了近似完全可靠信息,即以参数的最小二乘解XLS作为对称中心,以3倍中误差作为模糊幅度。如图1所示,在误差理论中,X∉[XLS-3δXLS,XLS+3δXLS]的概率为0.3%,属于小概率事件[17]。因此将参数X的参考信息构造为[XLS-3δXLS,XLS+3δXLS],模糊数形式写为[XLS,3δXLS]。
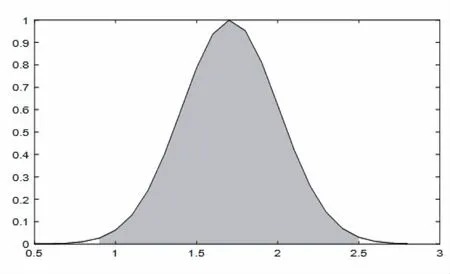
图1 可靠信息分布
2.2 可信度的计算
可信度R是衡量先验信息可靠性的指标,将其引入参数估计时,应满足以下条件:
(1)0≤R≤1;
(2)当R越大,先验信息越可靠,在参数估计过程中起的作用越大;反之,R越小,先验信息越不可靠,在参数估计过程中起的作用越小;
(3)当R=0时,先验信息完全不可靠;R=1时,先验信息完全可靠。
模糊理论中贴近度q表示两模糊集的接近程度,引申到测量学中,若先验信息与参考信息越接近,则可认为先验信息的可信度越高,且贴近度q完全符合以上条件,因此采用贴近度来衡量先验信息的可靠性是合理的,即令
R=q
(2)
上文中构造参数的参考信息为[XLS,3δXLS],将参数X的先验信息记为[X0,δx]结合式(1)与式(2),若XLS>X0,可得出先验信息可信度的计算公式为:
(3)
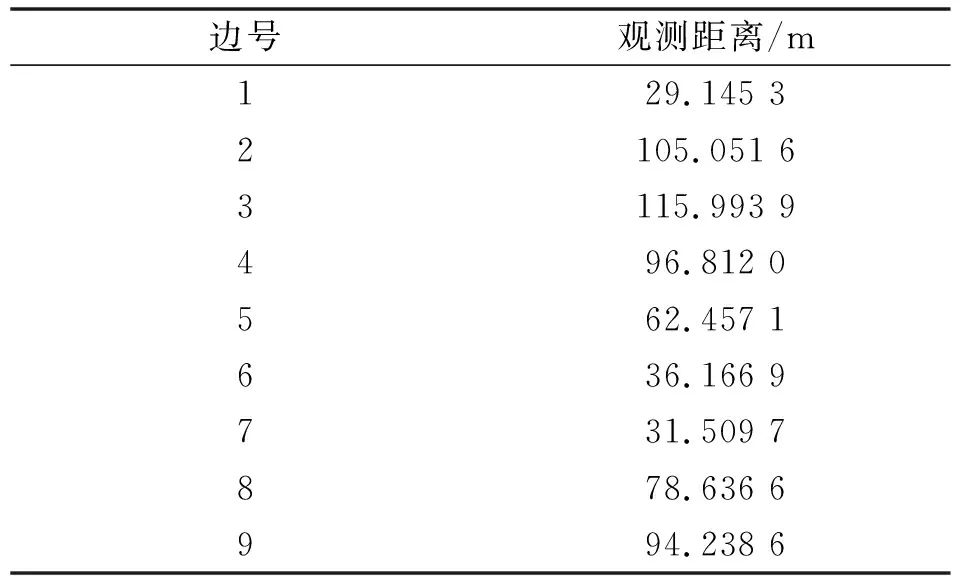
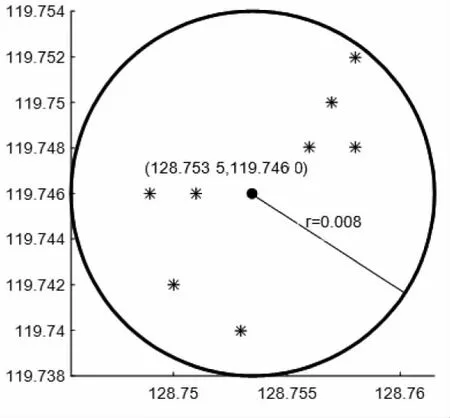
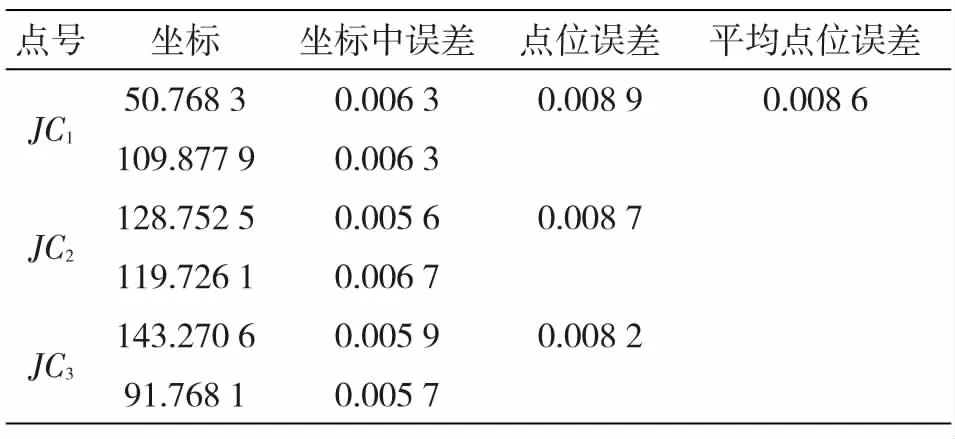
若XLS (4) 式中,X0为先验信息提供的参数中心值,δx为模糊幅度,表示其变动范围。XLS和δXLS为参数最小二乘解及其中误差。 建立附有模糊先验信息的平差模型为: L=AX,X∈[X0,δx] (5) 式中,L为n维观测向量,A为n×m维系数矩阵,X为m维参数向量,X0和δx表示先验信息提供的参数中心值以及模糊幅度。建立估计准则: min:f(X)=(AX-L)TP(AX-L)TP(AX-L)+(X-X0)TPX(X-X0) (6) 式中,P为观测信息权阵,PX表示参数的先验权阵,X0为先验信息提供的参数中心值。本文将可信度R以先验权阵PX的形式纳入到参数估计过程中,以平衡不同可信度先验信息在参数估计中的作用,具体步骤如下: 第一步:求得参数X的最小二乘解: XLS=(ATPA)-1ATPL (7) 及其相应的中误差阵[20]为: (8) 式中,δ0为单位权中误差,δXLS为参数X的中误差; 第二步:根据上文所述,构造参考信息,记为模糊数形式为[XLS,3δXLS]; 第三步:将先验信息记为模糊数形式并根据式(3)或式(4)求解先验信息与参考信息的贴近度R1,2,…m; 第四步:将第三步计算得到的贴近度R1,2,…m,构成为先验权阵PX,即令PX=diag(R1,R2,…,Rm),将式(6)对参数X求偏导并令其等于零得: 2(AX-L)TPA+2(X-X0)TPX=0 (9) 令N=ATPA+PX,由上式推导得参数X的计算公式为: X=N-1(ATPL+PXX0) (10) 其协因数阵为: Qxx=N-1 (11) 式中,X0为先验信息提供的参数中心值,PX为先验信息权阵。该算法的实质是充分利用最小二乘估计的结果对先验信息的可靠性进行评估与度量,选取更加合理的先验权阵来合理利用先验信息中的可靠成分并抑制不可靠成分的影响。 为了验证算法的有效性,本文通过直线方程y=1.6x生成一个不含误差的数据列,然后在这些数据列中加入随机误差,得到一组模拟观测值列于表1内。 表1 模拟数据 由表1产生的数据构造观测向量L=[y1y2y3y4y5]T和设计矩阵A=[x1x2x3x4x5]T并建立平差模型为: L=AX (12) (1)求得最小二乘解及其偏差为: (2)利用本文所提加权算法进行解算,过程如下: σXLS=0.266 7 第二步:构造参考信息为[1.706 8,0.800 1]; 第三步:确定先验信息可信度R=0.607 4; 第四步:取观测权阵P=I,令PX=diag(R),代入式(10)得参数解及其偏差: (3)取PX=I,认为先验信息完全可靠。代入式(10)得到参数解及其偏差: 图2 拟合直线 图3 数据点残差分布 由上面计算结果可得如下结论: (1)由图2、图3可知,本文所提顾及先验信息可靠性的加权算法拟合直线效果明显优于最小二乘拟合以及不考虑先验信息可靠性拟合; 先验信息的可信度用来衡量先验信息的可靠程度,不确定度用来衡量先验信息的精度。先验信息的可靠性对参数估计有着重要影响,而先验信息的精度约束同样是参数估计中的关键问题,随着先验信息模糊幅度的增大,由式(3)及式(4)可知,先验信息的可靠性会逐步增大,但同时先验信息约束效力也会随之减弱。因此为了探究先验信息不确定度与先验信息可信度及参数估计精度之间的关系,本文通过多次改变先验信息的模糊幅度进行参数平差,得到先验信息模糊幅度与先验信息可信度及参数估计解残差的关系如图4所示。 图4 模糊幅度与可信度及参数残差之间的关系 当不考虑先验信息进行最小二乘平差时,最小二乘解的残差为0.106 8。由图4分析可知: (1)先验信息的可信度与不确定度正相关,当模糊幅度趋于无穷大时,先验信息可信度虽然趋近于1,但此时先验信息已没有约束效力,因此在顾及先验信息的可靠性进行加权平差时,还需考量先验信息的精度; (2)随着先验信息的模糊幅度增大,虽然先验信息可信度增高,但此时参数估计残差也随之缓慢增涨,说明先验信息的精度与可靠同时对参数估计精度有着影响; (3)当先验信息模糊幅度小于2.5时,先验信息可信度位于0.7左右,本文所提加权算法可显著提高参数估计精度;当模糊幅度大于10以后,可信度对于参数估计精度提高效果均不明显;当模糊幅度大于20以后,考虑先验信息进行平差计算已没有意义,说明此时先验信息的不确定度对参数估计精度的影响已远远大于先验信息可靠性的影响。 因此可知,先验信息的精度对参数估计精度也有着重要影响,在先验信息精度不足的情况下考虑先验信息可靠性是没有意义的。本文分析讨论了先验信息可靠性对参数估计的影响,但未考虑先验信息不确定度的作用,如何进一步将先验信息不确定度与可靠性同时纳入参数估计过程以提高参数估计效率,有待进一步研究。 本文选取某工程2013年变形监测所布设的监测网如图5所示。其中,M1,M2为两个基准点,坐标分别为(27.288,92.588)/m和(132.072,57.400)/m,JC1,JC2,JC3为三个监测点。该工程在监测期间,采用徕卡TC402型全站仪(测角精度为2 S,测距误差为2 mm+2 ppm)进行周期性重复测量,观测边长列于表2。要求根据观测距离确定各监测点的坐标。 图5 测边网 边号观测距离/m129.145 32105.051 63115.993 9496.812 0562.457 1636.166 9731.509 7878.636 6994.238 6 依照上文所述步骤进行网平差。 第一步:进行最小二乘估计,结果及点位如表3所示。 第二步:构造参考信息,写为模糊数形式为: 图6 点JC1分布图 图7 点JC2分布 图8 点JC3分布 则可将先验信息表示为: 由式(3)和式(4)计算得到先验信息XZ与第三步构造的参考信息XK的贴近度为: R=[0.692 2 0.715 4 0.937 5 0.627 1 0.819 9 0.869 2]T; 表3 最小二乘平差结果/m 表4 加权算法平差结果/m 通过表3、表4分析比较,顾及先验信息可靠性的加权算法平差结果较之经典最小二乘,监测点JC1、JC2、JC3的坐标中误差及点位误差均有大幅度减小,顾及先验信息可靠性的加权算法可以有效提高参数估计精度。 本文针对大地测量学中先验信息存在的不确定性以及可靠性问题,尝试采用模糊数集来描述先验信息,用模糊幅度表征其不确定性,并基于小概率事件原理构造参考信息,运用先验信息与参考信息的模糊贴近度来衡量先验信息的可靠性并论证了其合理性,给出了可信度的计算公式,将其以权阵的形式纳入估计过程以平衡不同可信度的先验信息在参数估计中的作用,实例验证了本文所提算法不仅能够合理的利用先验信息,提高参数估计精度,且一定程度上抑制了不可靠成分对参数估计的影响。3 模型解算
4 算例分析
4.1 模拟算例




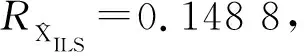
4.2 先验信息的不确定度约束

4.3 工程实例






5 结 论

