自承式钢管跨越结构鞍式支承处管壁环向弯曲应力分析

黄承辉

上海市政工程设计研究总院（集团）有限公司 200092

引言

自承式钢管跨越结构作为给水管道穿越河流等障碍物的一种常用型式，具有施工难度小、工期短、施工质量易保障和安全可靠等优点，在合适的跨度内，钢管结构造价较低。但在实际工程中，受河道通航、景观等因素限制，钢管的跨度通常较大，限制了自承式钢管跨越结构的使用。往往需加大钢管壁厚，或者采用钢桁架型式承重，在承载桁架上设置钢管支承，减小钢管跨度，但该型式造价较高，设计与施工也较复杂。

自承式钢管跨越结构的计算可简化为单跨或多跨连续梁，总应力最大值一般位于钢管支承处，其中管壁的环向弯曲应力对支承处总应力的影响较大。目前钢管跨越结构的设计通常是按照《自承式给水钢管跨越结构设计规程》（CECS 214—2006）［1］进行计算分析，本文应用ANSYS有限元软件对支承处管壁的环向弯曲应力进行研究，发现根据规程计算的环向弯曲应力远大于实际应力［2，3］。已有研究，基于Winkler地基的自承式钢管桥三维有限元数值计算表明，鞍式支承处管壁环向最大弯矩的规范计算结果数倍于数值计算结果［4］。为此，本文提出了环向弯曲应力的优化推荐算法，并通过不同支承宽度、管径、壁厚和支承半角变量下的计算结果进行验证。

1 自承式钢管可滑移支承

为研究支承处管壁的环向弯曲应力，首先应分析钢管的支承型式。考虑管道的温度应力，对不同跨数的管道，需合理布置可滑移支承。根据《市政给水管道工程及附属设施》图集07MS101-3，管径D≤500mm，采用鞍式可滑移支承，钢管与弧形垫板间满涂特种润滑脂；管径600mm≤D≤1000mm 时，采用鞍式滚动可滑移支承，钢管与弧形托板满焊，辊轴垫槽中填满特种润滑脂；管径D≥1000mm 时，宜用设有侧向支撑环的滚动可滑移支承，钢管与弧形托板满焊，辊轴垫槽中填满特种润滑脂。

本文主要研究600mm≤D≤1000mm的钢管，根据图集07MS101-3，若采用混凝土支承，支承尺寸沿管道轴向的长度为890mm～1130mm，垂直向宽度为1350mm～2350mm，混凝土支承体量大，经济性较差，且还需设置辊轴和垫槽，施工也较为繁琐。在实际工程中，钢管常采用钢托架作为滑动支承，弧形钢板与钢管间设置橡胶垫，实现温度应力下钢管沿轴线方向的自由滑动，做法示意见图1。

图1 DN800 钢管托Fig.1 Brackets for DN800 steel pipe

钢管托尺寸较小，经济性好，且施工便利，应用广泛。但由于支承宽度较小，根据规范计算支承处的管道环向弯曲应力较大，支承处管道的折算应力相应较大，需要对支承处相关范围内的钢管管壁进行局部加厚。下文对该支承型式的管道环向弯曲应力进行研究，找出优化应力的计算方法，减小管道壁厚。

2 支承处环向弯曲应力规范计算

钢管跨越结构所受荷载包括管道自重、管道内水重、管内静水压力、风荷载和温度作用等，在竖向荷载作用下，钢管的计算可以简化为一根连续梁，支承处应力通常起控制作用，根据《自承式给水钢管跨越结构设计规程》，钢管管壁的截面最大组合折算应力可按：

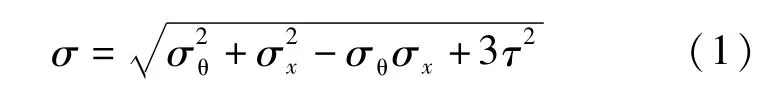
式中：σ为管壁截面的最大组合折算应力；σθ为管壁截面的环向拉应力；σx为管壁截面的纵向应力；τ为管壁截面的剪应力。

式中：Mθ为鞍式支承的管壁环向弯矩；Wr为鞍式支承的管壁截面抵抗矩；t为支承处钢管壁厚；Bs为钢管的实际支承宽度。

由此，可计算出钢管在自重和满水荷载下支承处管壁A、B、C 点处的环向弯曲应力，各点位置见图2。

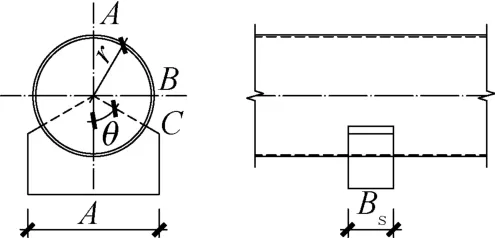
图2 钢管支承截面Fig.2 Section of steel pipe support

3 支承处环向弯曲应力有限元计算

本文应用ANSYS 软件对自承式钢管跨越结构进行有限元分析，钢管采用shell63 壳单元，材料本构关系为线弹性模型，根据钢管跨度和支承布置情况，建立整体有限元模型。荷载为钢管自重及管内水重，模型中通过钢管等效密度的方式施加，约束条件为支承范围内各节点的径向位移约束，轴向与环向无位移约束。

计算所得钢管环向弯曲应力如图3 所示。

图3 支承处环向弯曲应力云图（单位：N/m2）Fig.3 Hoop bending stress at support（unit：N/m2）

由图3可以看出，最大环向弯曲应力主要集中于钢管支承处；各点应力取值方法为：A点和B点处，直接取最大应力值；C点处应力受点约束影响出现应力集中，应力值取内外表面应力的平均值。

4 支承处环向弯曲应力推荐计算

环向弯曲应力主要取决于环向弯矩以及相应的截面抵抗矩，其中环向弯矩Mθ为实际支承宽度Bs范围内的环向弯矩总和，计算公式为：

式中：k为鞍式支承处管壁的环向弯矩系数；R为支承宽度Bs的支座反力。在跨度和管径r一定的情况下，支座反力是确定的，即可得出Mθ；而对于管壁截面抵抗矩，规范采用钢管支承的实际宽度进行计算，然而一般支承影响长度要大于实际的支承宽度。

本文以一座五跨DN800 自承式钢管为例，计算支承处管壁的环向弯曲应力，其中钢管跨度为20m，壁厚为14mm，支承半角θ 为60°，如图4 所示。

图4 五跨DN800 自承式钢管Fig.4 Five spans of DN800 pipe bridge

设置支承宽度为变量，分别按规范公式和有限元方法进行计算，结果见图5。

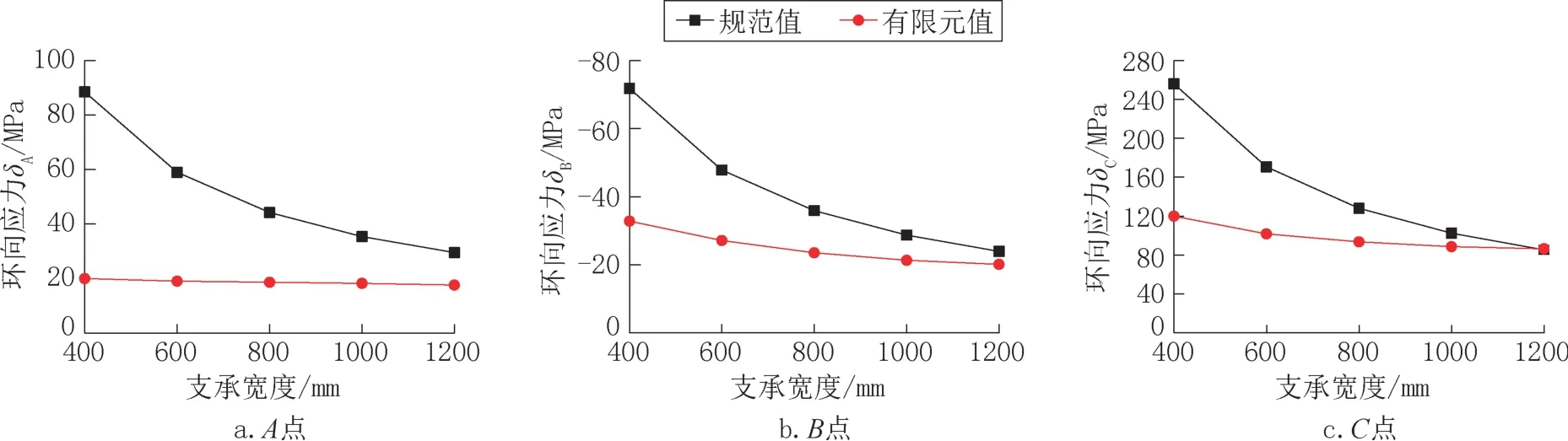
图5 环向弯曲应力（θ=60°）Fig.5 Hoop bending stress（θ=60°）

由图5 可见，对于规范环向弯曲应力，与支承宽度成反比例变化关系，如A 点环向弯曲应力，600mm 支承宽度时应力约为60MPa，1200mm支承宽度时应力约为30MPa；而对于有限元计算结果，虽然钢管各点环向弯曲应力随着支承宽度增大而减小，但两者为不等比例变化关系，且随着支承宽度增大，环向弯曲应力趋近稳定值，如C点环向弯曲应力；通过各点环向弯曲应力图可以发现，各支承宽度下有限元计算的最大应力所对应规范算法的支承宽度约为800mm，即一倍钢管直径。

在此基础上，本文提出了一种鞍式滑动支承的管壁环向弯曲应力计算方法：环向弯矩的计算采用规范算法保持不变，而支承影响长度取为钢管直径，同时不小于钢管的实际支承宽度Bs。钢管应力的主要影响因素为钢管跨度、管道支承半角、钢管管径、钢管壁厚和支承宽度，本文不考虑钢管跨度的影响，分别对其余四个因素进行控制变量计算分析，进一步验证推荐计算方法的安全性和适用性。

4.1 不同支承宽度下环向弯曲应力计算和分析

钢管支承宽度直接影响支承弯矩的截面抵抗矩，支承宽度Bs分别取400mm、600mm、800mm、1000mm和1200mm，由此可根据推荐算法得到不同支承宽度下的环向弯曲应力，见图6。

由图6 可见，钢管各点环向弯曲应力随着支承宽度增大而减小；当支承宽度不大于1000mm时，规范及推荐计算应力结果均大于有限元计算结果，即推荐环向弯曲应力计算结果偏于安全；当支承宽度大于1000mm 时，C点处规范及推荐计算应力结果开始小于有限元计算结果；因此，在支承宽度不大于1000mm时，推荐方法适用。

图6 不同支承宽度下环向弯曲应力（θ=60°）Fig.6 Hoop bending stress under different bearing width（θ=60°）

4.2 不同管径下环向弯曲应力计算和分析

管径的变化直接影响管道内水重，从而影响支承环向弯矩；同时，管径也会影响支承影响长度。本文研究的管道管径范围为600mm≤D≤1000mm，取工程常用支承半角为60°，支承宽度Bs为0.4m，余参数同前算例，计算A、B 和C点处的钢管环向弯曲应力，结果见图7。

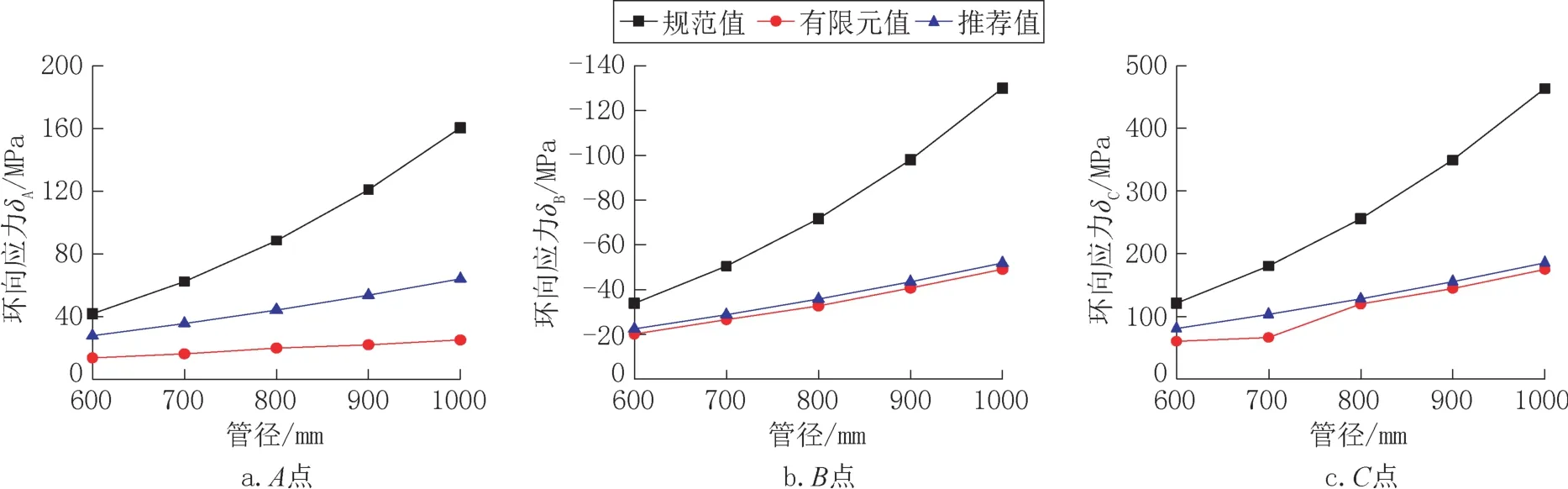
图7 不同管径下环向弯曲应力（θ=60°）Fig.7 Hoop bending stress under different pipe diameter（θ=60°）

由图7可见，钢管各点环向弯曲应力随着钢管直径的增大而增大；对于同一计算点，推荐计算方法所得环向弯曲应力值介于规范算法和有限元计算值之间，其中B点和C点处应力与有限元计算结果吻合较好，可见采用推荐算法较规范算法有较大的优化，且计算结果仍能保证安全。因此，在600mm≤D≤1000mm管径范围内，推荐方法适用。

4.3 不同壁厚下环向弯曲应力计算和分析

钢管壁厚主要影响支承弯矩的截面抵抗矩，本文钢管壁厚分别取12mm、14mm、16mm、18mm和20mm，取工程常用支承半角为60°，支承宽度Bs为0.4m，余参数同前算例，计算A、B和C点处的钢管环向弯曲应力，结果见图8。

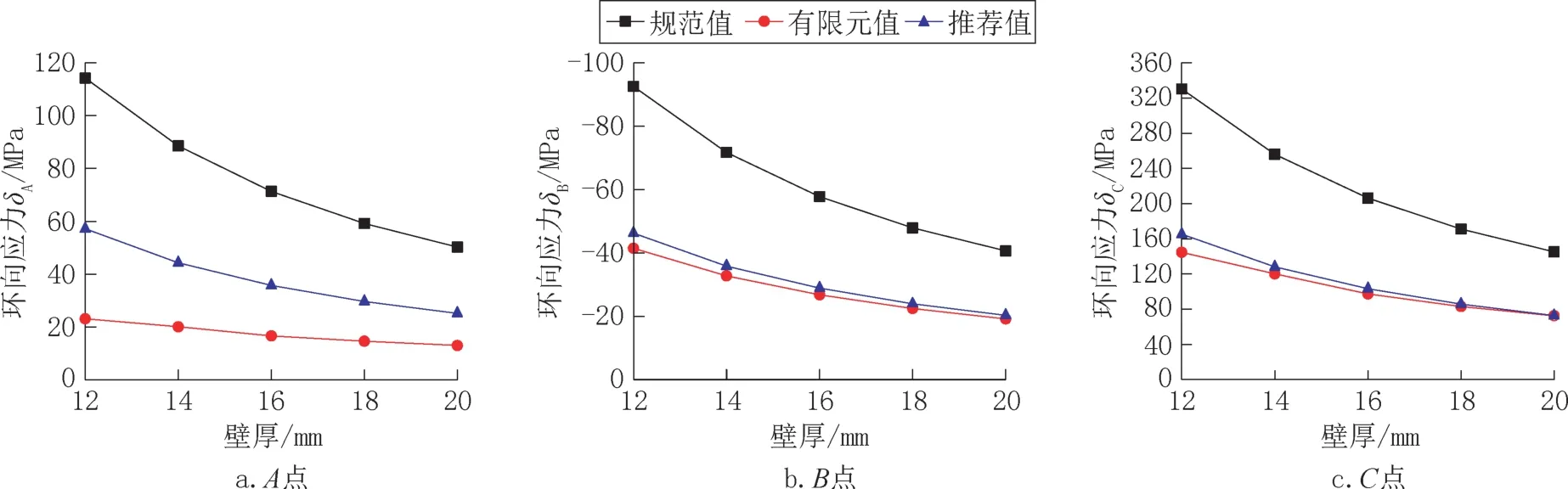
图8 不同壁厚下环向弯曲应力（θ=60°）Fig.8 Hoop bending stress under different pipe thickness（θ=60°）

对比可见，钢管各点环向弯曲应力随着钢管壁厚增大而减小；对于同一计算点，推荐计算方法所得环向弯曲应力值介于规范算法和有限元计算值之间，其中B点和C点处应力与有限元计算结果吻合较好，因此，在不同壁厚下，推荐方法适用。

4.4 不同支承半角下环向弯曲应力计算和分析

不同的支承半角直接影响支承处管道的环向弯矩，对前例中的DN800 钢管，取支承宽度为0.4m，根据推荐算法，支承影响长度取钢管直径与Bs两者中的大值，为800mm，由此可分别得出规范算法、有限元计算和推荐算法在不同支承半角下的环向弯曲应力，见图9。

由图9 可见，三种算法得出的管壁环向弯曲应力的变化规律一致，A点和C 点应力均随着支承半角增大而减小，且同一截面中C 点应力最大，A点应力最小；B点应力随着支承半角增大，外表面应力由拉应力变为压应力；对于同一计算点，推荐计算方法所得环向弯曲应力值介于规范算法和有限元计算值之间，其中B点和C点处应力与有限元计算结果吻合较好。因此，在不同支承半角情况下，推荐方法也适用。

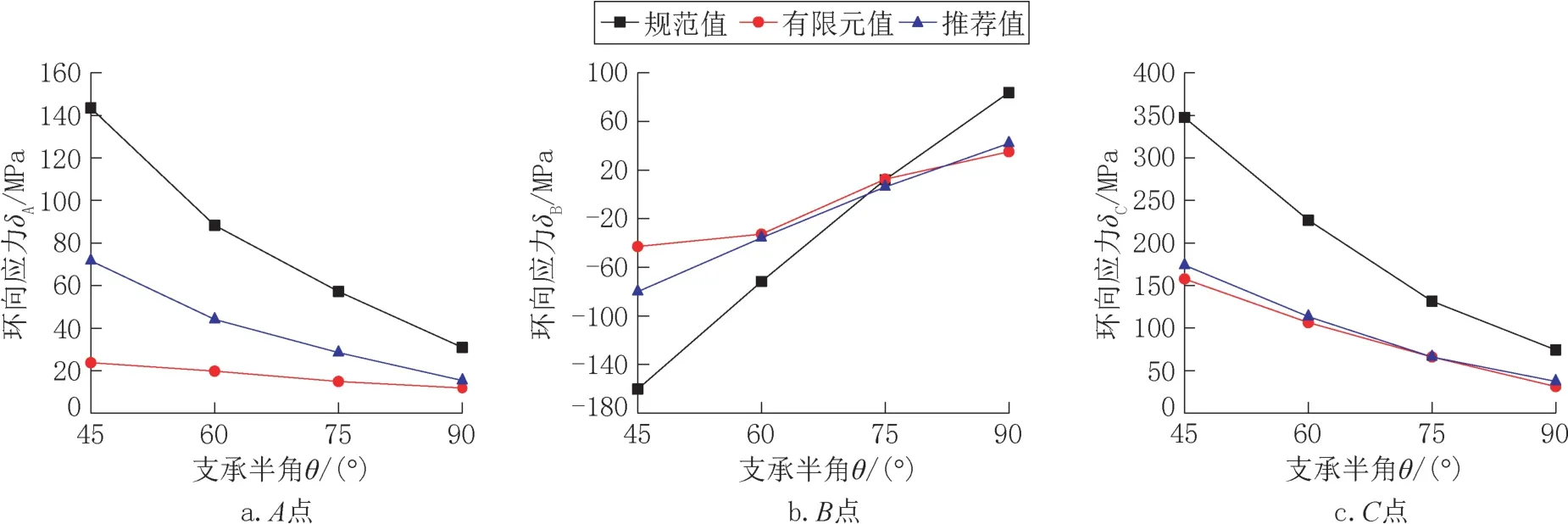
图9 不同支承半角下环向弯曲应力Fig.9 Hoop bending stress under different bearing half angel

5 结论

1.管径为600mm≤D≤1000mm 的自承式钢管支承处管壁的环向弯曲应力为：环向弯矩的计算采用规范算法保持不变，而环向截面抵抗矩中的支承影响长度取为钢管直径，且不小于钢管的实际支承宽度。

2.钢管支承处环向弯曲应力与实际支承宽度为不等比例变化关系，随着支承宽度的增大，环向弯曲应力趋近稳定值，建议钢管的实际支承宽度不大于1000mm。

3.通过环向弯曲应力的优化计算，一方面对相同跨度下的钢管，能优化钢管壁厚；另一方面在相同壁厚下，加大了钢管的允许跨度，扩大自承式钢管跨越结构的适用范围。