超规范高宽比矩形烟囱风压与风振系数分布研究*

李旭 刘兵 王君鹏

山东电力工程咨询院有限公司 济南250013

引言

烟囱是以承受风荷载为主的典型高耸空间薄壳结构，其在强风作用下的安全性历来受到工程界的高度重视［1，2］。近年来，随着我国电力工业的不断发展和国家环境保护标准的不断提高，新建核力/火力发电厂和垃圾发电厂均需要烟雾过滤/脱硫处理，为满足环保要求，烟囱不断向超高方向发展，超规范高宽比问题随之而来［3，4］。超规范高宽比烟囱结构特有形状极易诱发较大的风振响应［5，6］，现有规范［7-9］高宽比在4～8 之间的规定已不能满足拟建工程需求，再考虑到现有针对烟囱风荷载研究大多聚焦于圆形截面，而矩形烟囱的流动分离和风压分布与其差异较大。因此，超规范矩形烟囱风压分布特性与风振系数取值是矩形烟囱实现跨越式发展而亟待解决的瓶颈问题。

现有关于高耸烟囱结构的研究多以圆形截面自立式［10-14］或多管集束式烟囱［15-18］为对象，杨群等［10］采用数值模拟开展了不同间距圆形截面三管钢烟囱的风荷载研究；Gorski等［13］采用数值仿真研究了波兰295m 工业烟囱在紊流作用下由横向紊流分量和涡激引起的非线性气动阻尼力，并提出了横向湍流分量响应的功率谱密度函数；Sanada等［13］对200m混凝土烟囱周围的风压及相关的挠度和振动开展了系统性分析，并探究了烟囱的横风向风振效应；刘庆宽等［14］探究了超高圆形截面烟囱的风荷载及风致振动特性；柯世堂等［15］通过刚体测压风洞试验研究了180m三管集束式钢烟囱风致响应与风振系数。国内外目前关于针对超规范高宽比矩形烟囱的抗风研究较少，张纯康等［16］研究了某矩形截面烟囱的附加弯矩和开口处应力，但未开展对超高宽比矩形烟囱的风压分布和风振系数等研究，严重制约了矩形烟囱结构抗风的设计能力提升。

鉴于此，以国内某拟建核电站超规范高宽比矩形烟囱为研究对象，针对三种高宽比方案分别建立结构模型并开展动力特性分析，采用STAR CCM+平台开展双向流固耦合的精细化数值仿真，分析烟囱的风压分布特性、结构升力及阻力系数、气流绕流特性和涡量分布特性，探讨三种方案下烟囱的顶部位移、底部剪力和横风向位移响应变化规律，并给出了不同方案烟囱风振系数及整体风振系数取值，可为超规范高宽比矩形截面烟囱的工程设计和振动控制提供重要的参考依据。

1 工程概况

1.1 设计条件

该拟建核电站超规范矩形烟囱位于河北省石家庄市，地貌类型为B类，10m高度处重现期为50 年的基本风压为0.35kN/m2，对应基本风速为23.89m/s。烟囱沿子午线总高度为100m，筒壁自下而上采用变梯台壁厚形式，从塔底向上0～34m壁厚为350mm，34m～100m 壁厚为300mm。矩形烟囱外壁混凝土等级为C45，材料密度为2410kg/m3，材料弹性模量为3.35 ×1010Pa，泊松比为0.2。

1.2 方案设置

为满足烟囱环保排放标准，该拟建工程的设计高宽比在10～16 之间，规范［7］对矩形截面高耸建筑横风向荷载计算的限定高宽比在4～8 之间，该拟建矩形截面烟囱高宽比已超出规范允许值。为探究不同高宽比对超规范矩形截面烟囱的风压分布特性与风振响应的影响，针对该拟建项目设置三种研究方案，表1 给出了超规范矩形截面烟囱三种方案主要结构尺寸。

1.3 几何模型与动力特性

建立超规范矩形截面烟囱三种方案足尺实体模型，超规范矩形烟囱底面与水平地面采用固定约束，限制烟囱底面各方向自由度，几何模型的总体坐标系以沿子午向为Z 轴，顺风向为X 轴，横风向为Y轴，符合右手定则。采用Modal Analysis Module方法对三种方案矩形烟囱开展动力特性分析，图1 给出了三种方案超规范矩形烟囱前100 阶自振频率对比曲线，由图可知，三种方案烟囱自振频率宏观上均近似呈对数增长趋势，随着矩形烟囱高宽比增大，矩形烟囱前100 阶自振频率呈现显著增大。

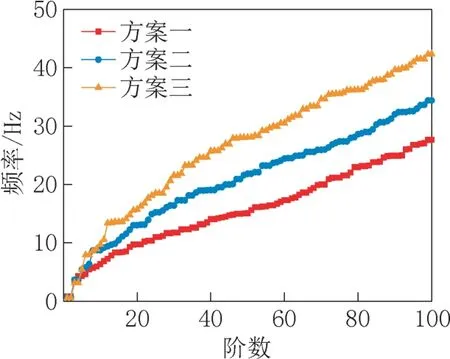
图1 前100 阶自振频率对比曲线Fig.1 Comparison curves of first 100 order natural frequency

表2 给出了三种方案超规范矩形烟囱几何模型和典型模态。烟囱的自振频率与张纯康等［16］研究的超高矩形烟囱频率相近，验证了结构模态的准确性。由表可知，三种方案下烟囱第一阶振型形式均呈现为近似的摆动姿态，第三阶和第五阶呈现为扭转或弯曲模态。烟囱第1 阶固有频率随高宽比增大而减小，前100 阶自振频率随高宽比增大而增大，说明高宽比越大，烟囱自振频率越发散。

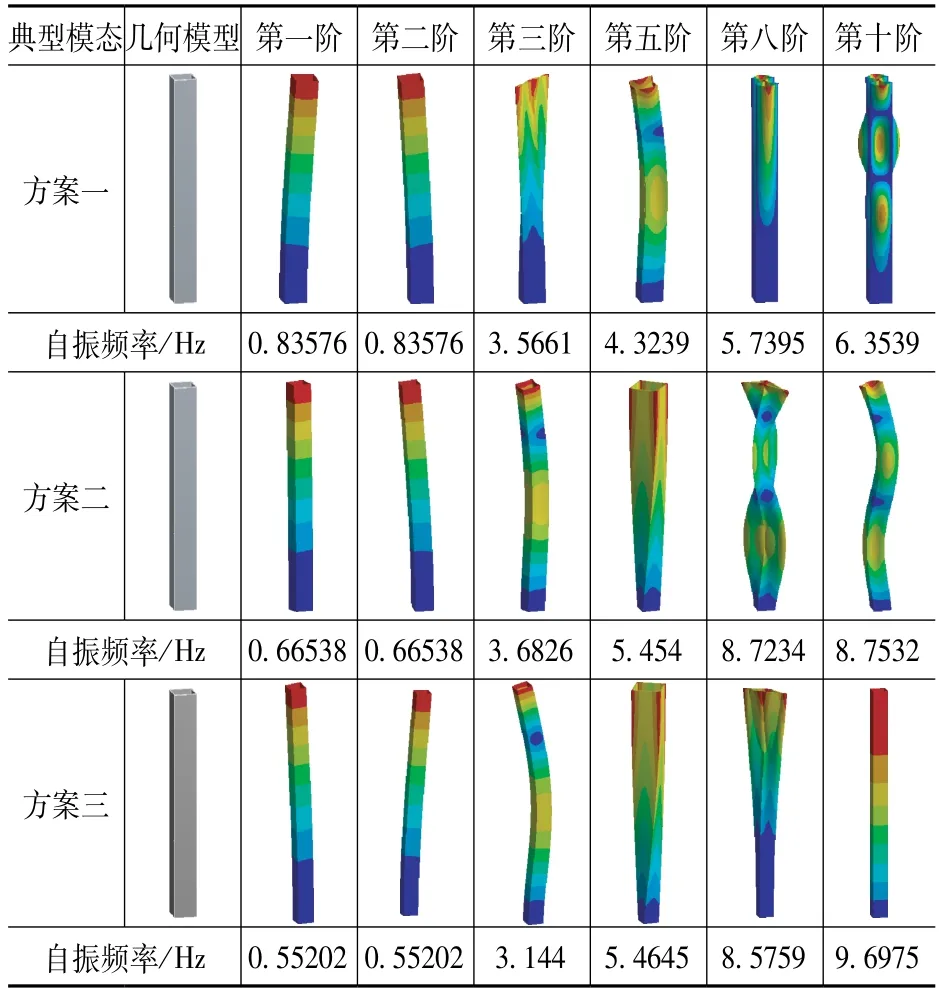
表2 烟囱几何模型和典型模态Tab.2 Geometric models and typical modes of chimney

2 数值风洞试验

2.1 计算域及网格划分

现有关于结构与流体的研究多采用ANSYS与Fluid进行单向荷载传递，不能考虑结构自身变形对流场的干扰。STAR CCM +软件可通过网格数据插值实现位移、变形等场变量交换。本文STAR CCM+平台开展双向流固耦合数值仿真分析，考虑风与结构的气弹效应，可对流场和结构变形进行精细化仿真。为保证空气流动可以充分发展，三种方案流体总计算域大小取1100m ×60m×250m（顺风向X ×横风向Y ×子午向Z），阻塞率满足小于5%的要求，计算模型中心距计算域入口为400m，出口位置距离模型700m。为了更好地兼顾计算效率与精度，将计算域划分为外围区域以及局部加密区域，外围区域形状规整，采用结构化网格进行划分；局部加密区域（200m×20m ×150m）及超规矩形烟囱模型采用更高质量的非结构化网格进行划分。加密区域最小网格尺寸为0.25m，各工况网格数量均为400万以上，网格数目及质量均满足计算要求，图2给出了流体计算域布局。

图2 流体计算域布局Fig.2 Schematic of calculation domain

2.2 控制方程

在进行结构抗风研究时，一般将流体被视为黏性且不可压缩，瞬态的N-S方程通过空间滤波可得到大涡模拟（LES）的控制方程［17］为：

基于Smagorinsky 提出的基于涡旋黏度假设的亚格子模型，引入Boussinesq 假设，则亚格子应力的表达式为：

本文研究的高雷诺数超规范矩形烟囱结构对大涡模拟的精度要求较高，采用Smagorinsky 亚格子模型开展高精度的数值模拟可达到较好的模拟效果［18］。

2.3 入流边界条件

计算域入口边界条件设置为速度入口（Velocity-Inlet），通过UDF 场函数定义上述脉动风场；出口采用压力出口边界条件（Pressure-Outlet），相对压力为零；计算域顶部和两个侧面采用自由滑移壁面的对称边界（Symmetry）；地面以及建筑物表面采用无滑移壁面边界条件（Wall）。

根据超规范矩形烟囱所处区域，计算域入口处速度剖面和湍流度采用指数率形式，沿高度方向变化的UDF场函数式为：

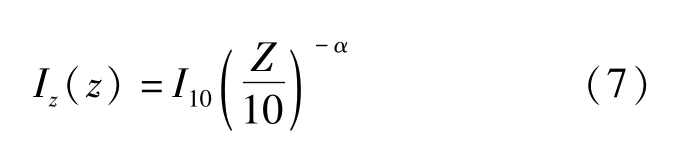
式中：U0为该地区Z0=10m高度处50 年重现期最大平均风速，取23.9m/s；Z 为计算高度距地面的距离；α 为B 类地貌地面粗糙度系数，取0.15；I10为10m高名义湍流度，取0.14。

空气风场选用不可压缩流场，同时采用SIMPLEC方法进行离散方程组的求解，该方法收敛性好且适合雷诺平均法计算，对流项求解格式为二阶，计算过程中设置了网格倾斜校正以提高混合网格计算效果。

2.4 有效性验证

表3 给出了三种方案超规范矩形烟囱与规范［7］中体型系数对比情况，由表可知，顺风向体型系数与规范接近且稍小于规范；横风向体型系数绝对值均稍大于规范值；背风向体型系数绝对值均小于规范值，整体而言，三种方案烟囱体形系数与规范值接近，验证了数值模拟试验的准确性。随着超规范烟囱高宽比增大，顺风向和背方向体型系数绝对值逐渐增大；横风向体型系数绝对值逐渐减小，这表明结构越细柔高耸，其受到的顺风向压力和背风向吸力越大，结构横风向受到的吸力反之减小，结构整体稳定性越差。

表3 烟囱体型系数与规范值对比Tab.3 Comparison of chimney shape coefficient and standard value

3 风压分布及流场特性

3.1 风压分布特性

表4 给出了三种方案超规范矩形烟囱顺风向、横风向和背风向风压分布云图，由图可知，矩形烟囱顺风向中部主要为正压区，其边缘与横风向相邻的极小区域呈现为负压，横风向和背风向主要以负压为主。矩形烟囱正压极值出现在顺风向；横风向风压分布不均匀，负压极值均出现在横风向；背风向风压较小且分布较为均匀，表明烟囱横风向部分区域负压产生的吸力已远超于背风向吸力。相同高度下，不同高宽比烟囱整体风压分布模式非常相似，仅在个别区域呈现较小差异。

表4 烟囱风压云图（单位：Pa）Tab.4 Wind pressure of chimney（unit：Pa）

图3 给出了三种方案超规范矩形烟囱纵向截面压力云图，由图可知，矩形烟囱顶部以上较大范围内呈现为负压，分析是由于流体在烟囱顶部的迎风端前缘分离造成的，烟囱内部和背风向均为负压为主。

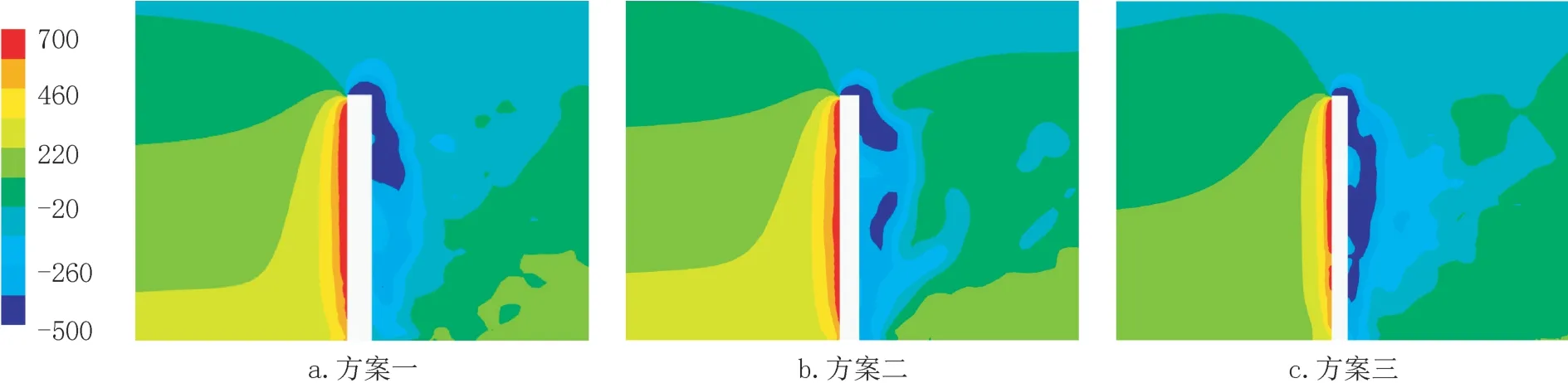
图3 烟囱周围平均压力云图（单位：Pa）Fig.3 Average pressure around chimney（unit：Pa）

3.2 升力及阻力系数

超规范矩形截面烟囱整体升力（横风向）和阻力（顺风向）系数［19］积分式计算如下：

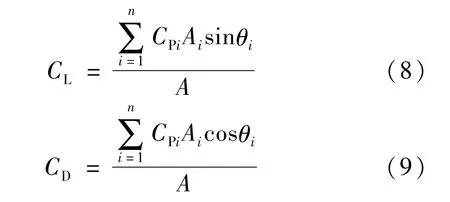
式中：CL、CD分别为结构整体升力和阻力系数；CPi为结构表面压力系数；Ai为第i个测点压力覆盖面积；θi为第i 个测点压力与风轴方向夹角；A为整体结构风轴方向投影面积。

图4 给出了三种方案矩形烟囱的阻力系数随高度变化曲线，由图可知，三种方案矩形烟囱的层升力及阻力系数均随高度的增加逐渐增大，并随烟囱高宽比的增大而逐渐减小。矩形烟囱层升力系数波动于-0.06～0.06 之间，并分别于高宽比为12.82 和15.38 时达到了最小值

图4 升力及阻力系数随高度变化曲线Fig.4 Curves of lift and resistance coefficients

-0.263 和最大值0.059；层阻力系数在高宽比为12.82 时达到了最大值1.108，高宽比为15.38时达到最小值0.670。

3.3 绕流特性

图5 给出了三种方案超规范矩形截面烟囱周围速度流线图，由图可知，气流沿矩形烟囱结构外壁加速效应比较明显，矩形烟囱顶部和横风向两侧出现流体加速现象，其中烟囱顶部以后区域平均速度最大；部分气流从烟囱顶部进入烟囱内部，但其流体速度很小，平均速度基本为0。烟囱背风向呈现多种尺度的涡流，并在约2 倍烟囱特征尺寸处消散，背风向气流扰乱区域随烟囱高宽比增大而逐渐减小，表明烟囱越高耸，背风向扰乱区域越容易从扰乱状态恢复为层流状态。

图5 烟囱周围速度流线图（单位：m/s）Fig.5 Velocity streamline around chimney（unit：m/s）

3.4 涡量分布特性

图6 给出了三种方案超规范矩形烟囱纵向截面涡量云图，由图可知，烟囱顺风向涡量强度较小，仅出现在近地面和顶部区域；烟囱涡量主要集中于背风向区域，涡量场中涡量的强度和涡的数量随着烟囱高宽比增大而减小。烟囱顶部和靠烟囱外壁面处涡量波动较大，说明涡量场具有贴壁特征。

图6 烟囱周围涡量分布云图（单位：m/s）Fig.6 Vorticity distribution around chimney（unit：m/s）

4 风致响应及风振系数

4.1 顶部位移风振系数

结构位移可以反映出矩形烟囱结构的变形状态，图7 给出了三种方案超规范矩形烟囱顶部90m高度以上的总位移。由图可知，矩形烟囱不同高度处的总位移平均值沿环形分布比较均匀，最大位移出现在顺风向顶部，横风向和背风向总位移较小，沿环向出现先减小后增大，而后又逐渐减小的趋势。

图7 烟囱顶部位移云图（单位：mm）Fig.7 Top displacement around chimney（unit：mm）

表5 给出了三种方案超规范矩形烟囱90m以上顶部位移的特征值及层平均风振系数。由表可知，超规范矩形烟囱顶部位移随高宽比增大而逐渐增大；风振系数沿子午向分布比较均匀，不同方案矩形烟囱风振系数随高度保持不变；不同高宽比矩形烟囱基于顶部位移的风振系数值均较小，最大仅为1.07。

表5 烟囱总位移及风振系数Tab.5 Total displacement and wind vibration coefficient of chimney

4.2 底部剪力风振系数

底部剪力是上部结构承受荷载大小的集中体现，表6 给出了三种方案超规范矩形烟囱底部剪力及其均方根。由表可知，超规范矩形烟囱顺风向底部剪力远大于横风向；随着烟囱高宽比增大，顺风向和横风向底部剪力均先增大后减小，其中横风向剪力值增大比例远大于顺风向剪力，分析是由于横风向底部剪力初始值较小造成的。超规范高宽比烟囱顺风向风振系数较小，横风向风振系数远大于顺风向风振系数，剪力合力风振系数较小，均分布于1.10～1.15 之间。

表6 烟囱底部剪力及风振系数Tab.6 Bottom shear and wind vibration coefficient of chimney

4.3 横风向位移风振系数

当气流绕过矩形建筑两侧时会产生交替的卡门旋涡，使建筑结构表面压力呈周期性变化，此时建筑物振动方向与风向垂直，形成横风向风振。图8 给出了三种方案横风向位移及风振系数沿高度分布曲线，由图可知，横风向位移均值随高宽比变化显著，30m高度处增长速度远大于其他高度增长速度。不同方案下的风振系数沿高度分布总体呈增长趋势，35m 高度处风振系数骤然减小，分析是由于烟囱变尺度壁厚引起的。风振系数取值随高宽比增大而增大，以横风向位移为目标的风振系数在数值上远远大于以顶部位移和底部剪力为目标的风振系数。

图8 烟囱横风向位移及风振系数Fig.8 Across-wind displacement and wind vibration coefficient of chimney

4.4 整体风振系数

基于超规范矩形截面烟囱以顶部位移、底部剪力和横风向位移为目标得到的风振响应及风振系数，得到超规矩形烟囱风振系数的整体风振系数取值，表7 给出了三种方案基于顶部位移、底部剪力和横风向位移为目标的整体风振系数取值。由表可知，以顶部位移和底部剪力为目标的风振系数远远小于以横风向位移为目标时的风振系数，三种方案超规范矩形烟囱整体风振系数最终建议取值为6.65、6.74 和8.73。研究表明，诸如矩形烟囱等超规范高宽比矩形结构的横风向风振响应非常显著且不容忽略，对超规范高宽比结构设计及振动控制时，应优先考虑结构横风向风振，并以横风向响应风振系数作为计算分析的等效目标。

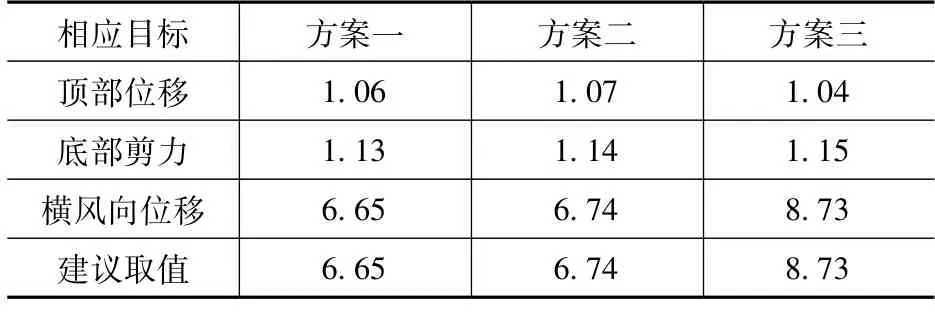
表7 烟囱整体风振系数Tab.7 Whole wind vibration coefficient of chimney

5 结论

采用STAR CCM+平台对超规范高宽比矩形烟囱开展双向流固耦合数值仿真，精细化分析了烟囱压力场、速度场和涡量场风压分布特性，以及顶部位移、底部剪力及风振系数变化规律，主要结论如下：

1.超规范矩形烟囱自振频率近似呈对数增长趋势，频率随着烟囱高宽比增大而增大，第1 阶固有频率随高宽比增大而减小，表明高宽比越小，自振频率分布越密集。

2.超规范矩形烟囱两侧横风向局部区域负压产生的吸力大于背风向吸力，顶部由于气流在迎风端前缘分离呈现负压；层升力及阻力系数均随高度增加逐渐增大，并随烟囱高宽比增大而逐渐减小。

3.气流经过超规范矩形烟囱结构顶部和两侧外壁加速效应比较明显；烟囱背风向呈现多种尺度的涡流，并在约2 倍烟囱特征尺寸处消散，涡量场中涡量的强度和数量随着烟囱高宽比增大而减小。

4.以横风向位移为目标的风振系数远大于以顶部位移和底部剪力为目标的风振系数，在设计建造和振动控制时应以横风向位移为目标考虑超规范高宽比烟囱风振。