高速铁路胶粘道砟固化道床的动力学特性
何 斌,肖 宏
(北京交通大学 土木建筑工程学院,北京 100044)
胶粘道砟最早在克罗地亚、比利时、德国[1]、日本[2]等国家应用,以达到增强道床纵横向阻力、防止道砟飞溅、稳定道床等目的。我国为了解决高速铁路道砟飞溅以及高速列车荷载作用下道砟颗粒粉化的问题,保证高速列车能够平稳安全地通过有砟轨道和无砟轨道过渡段,采用了道砟胶处理道床技术。通过将道砟胶注入到道床内部,将道砟颗粒黏结成整体,从而提高道床的整体稳定性,实现有砟轨道到无砟轨道的强度和刚度的平顺过渡。但是目前国内对胶粘道砟的力学特性研究以工程应用为主,理论研究相对较少。王浩宇等[3]就有砟-无砟过渡段采用胶粘道砟措施进行了初步的理论分析;王平等[4]通过轨道实尺模型试验,在实验室内测试了喷道砟胶前后道床纵横向阻力、支承刚度变化情况。
综上所述,有必要建立胶粘道砟固化道床模型,对道砟胶各项参数对道床力学性能的影响进行量化分析和总结。本文采用ABAQUS有限元软件,建立车辆-轨道空间耦合模型,展开胶粘道砟固化道床的动力学特性研究。
1 模型建立
采用ABAQUS有限元软件,针对高速铁路有砟轨道胶粘道砟固化道床和CRTSⅡ型板式无砟轨道过渡段建立车辆-轨道空间耦合模型,模型由车体、轮对、转向架、悬挂系统、钢轨、扣件、轨道板、CA砂浆层、底座板、道床、轨枕等部分组成。
1.1 车辆模型的建立
本文建立的车辆模型采用如下假定[5]:
1)将转向架和轮对视为刚体,对于运动过程中的弹性变形不予考虑。
2)列车、转向架和轮对的外形和质量采用对称设置,不考虑两边的偏差。
本文采用CRH3型车,为了充分模拟列车的荷载作用,建立了整车模型,综合考虑了一系和二系悬挂的垂向作用。一系和二系悬挂采用笛卡尔梁连接,2个转向架与车体之间采用MPC梁连接。
1.1.1 转向架和轮对模型
转向架采用离散刚体单元,因此不需要进行网格的划分。转向架不考虑纵向转动自由度,单个转向架的自由度为5,2个转向架的自由度合计为10。
因为轮对在计算时需要与钢轨进行表面接触,因此对轮对进行网格划分时采用解析刚体[6]。
根据我国高铁列车的主要机型参数,确定转向架和轮对的主要技术参数,包括沿x,y,z轴的转动惯量I11,I22,I33以及自身质量m。具体参数见表1。

表1 轮对和转向架技术参数
1.1.2 悬挂系统模型
悬挂系统采用弹簧-阻尼连接器单元进行模拟,弹簧和阻尼的性质设置为线性[7],具体参数见表2。
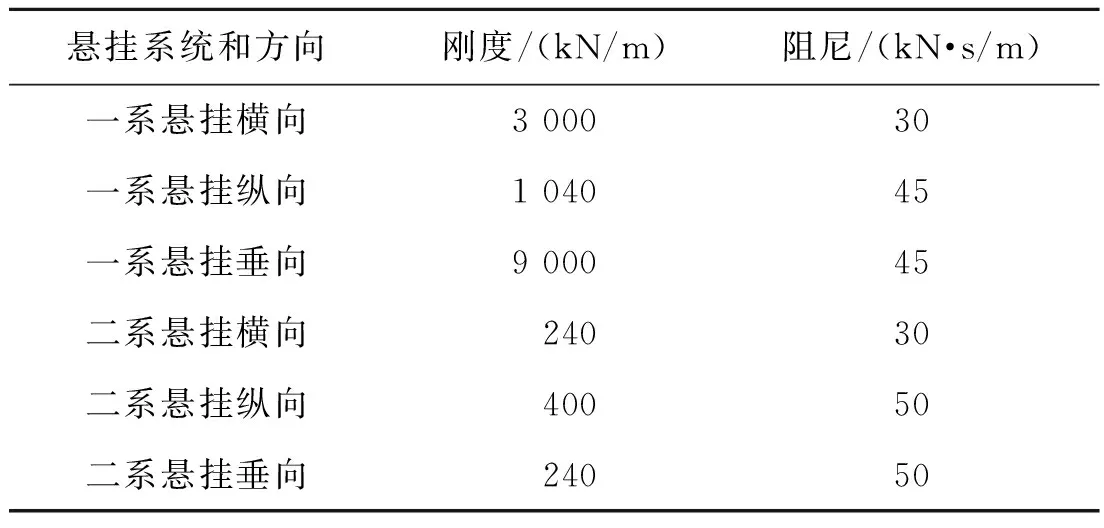
表2 悬挂系统参数
1.1.3 车体模型
本文所建立的车体模型不考虑车体的伸缩自由度,车体共具有横摆、点头、沉浮、摇头、侧滚5个自由度。
1.2 无砟轨道-有砟轨道模型的建立
1.2.1 胶粘道砟的模拟
在ABAQUS有限元软件中,可以通过改变道床的弹性模量和密度来模拟道砟胶的用量和固结深度的变化情况[8],以尽可能真实地模拟道砟胶对道床的影响情况[9]。
1.2.2 无砟轨道与有砟轨道的连接
由于无砟轨道和有砟轨道是不同的部件,将两者装配起来需要考虑两者之间的连接关系。装配时需要使两侧的钢轨位于同一水平面,两侧钢轨断面、道床断面和Ⅱ型轨道板断面之间都采用绑定连接,即连接后的整体能够共同受力和变形,符合实际情况中过渡段的受力和变形状态。道床和底座板的底面都施加全约束,模拟实际情况中下部基础的路基和桥梁[10]。最终确定的有砟轨道-无砟轨道过渡段模型如图1所示。

图1 有砟轨道-无砟轨道过渡段模型
2 道砟胶固化道床轨道过渡段动力学特性
2.1 道砟胶用量的影响分析
轨道结构的动力学分析主要包括道床应力、垂向动位移、垂向振动加速度等各项力学指标。采用普通碎石道床和道砟胶用量为36,48 kg/m3共3种工况进行对比,分析道砟胶用量对胶粘道砟固化道床轨道过渡段的动力学特性的影响规律。
2.1.1 普通碎石道床的动力学特性
表3为普通碎石道床动力学计算结果,可以看出,普通碎石道床在实际列车荷载的作用下,最大振动加速度为38.80 m/s2,最大垂向位移为1.56 mm,最大垂向动应力为0.13 MPa。
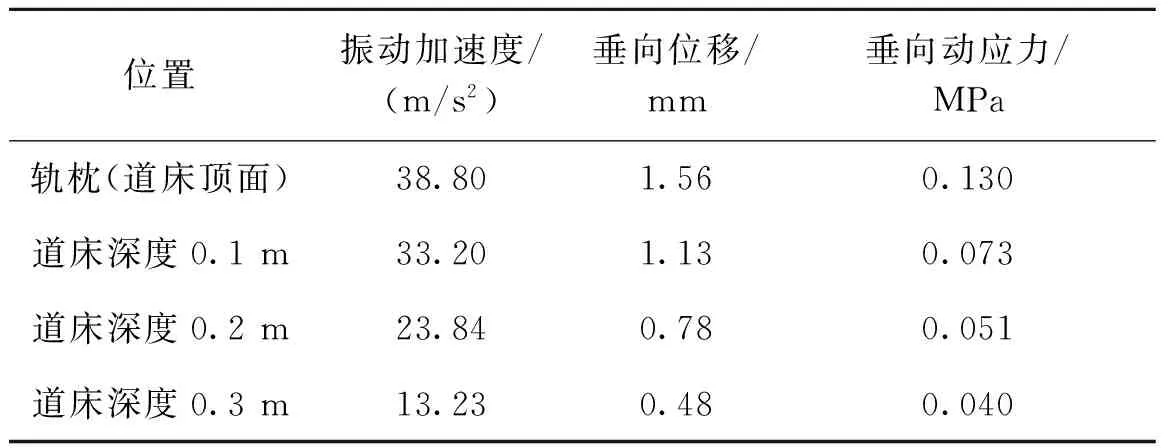
表3 普通碎石道床动力学计算结果
2.1.2 道砟胶用量36 kg/m3道床的动力学特性
表4为道砟胶用量36 kg/m3道床动力学计算结果,可以看出,道砟胶用量36 kg/m3道床在实际列车荷载的作用下,最大振动加速度为48.21 m/s2,最大垂向位移为1.25 mm,最大垂向动应力为0.21 MPa。
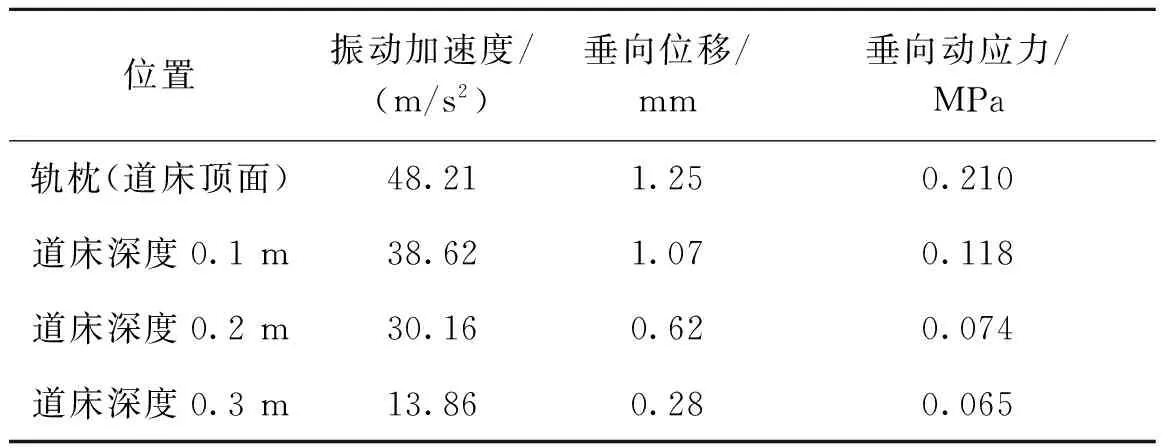
表4 道砟胶用量36 kg/m3道床动力学计算结果
2.1.3 道砟胶用量48 kg/m3道床的动力学特性
表5为道砟胶用量48 kg/m3道床动力学计算结果,可以看出,道砟胶用量48 kg/m3道床在实际列车荷载的作用下,最大的振动加速度为50.06 m/s2,最大垂向位移为1.18 mm,最大垂向动应力为0.26 MPa。
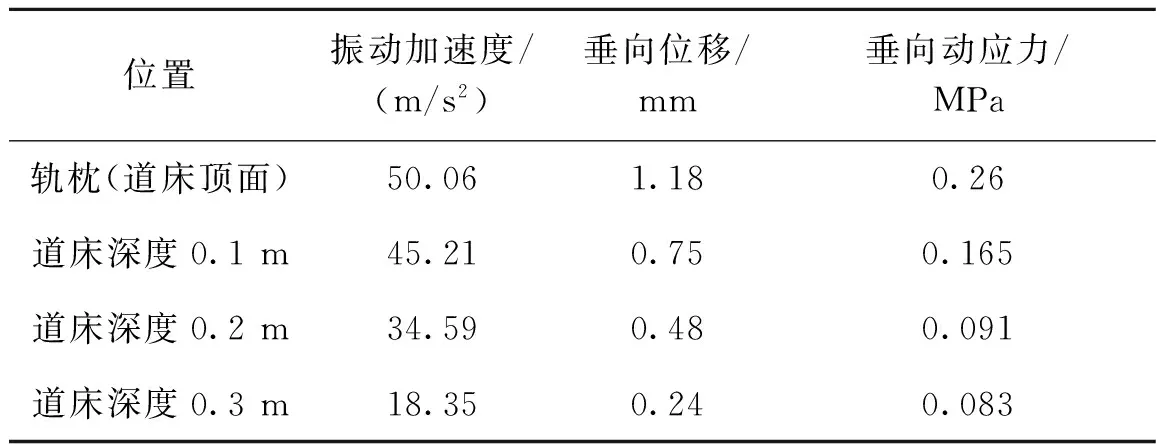
表5 道砟胶用量48 kg/m3道床动力学计算结果
2.1.4 不同道砟胶用量道床动力学结果对比分析
1)加速度对比分析
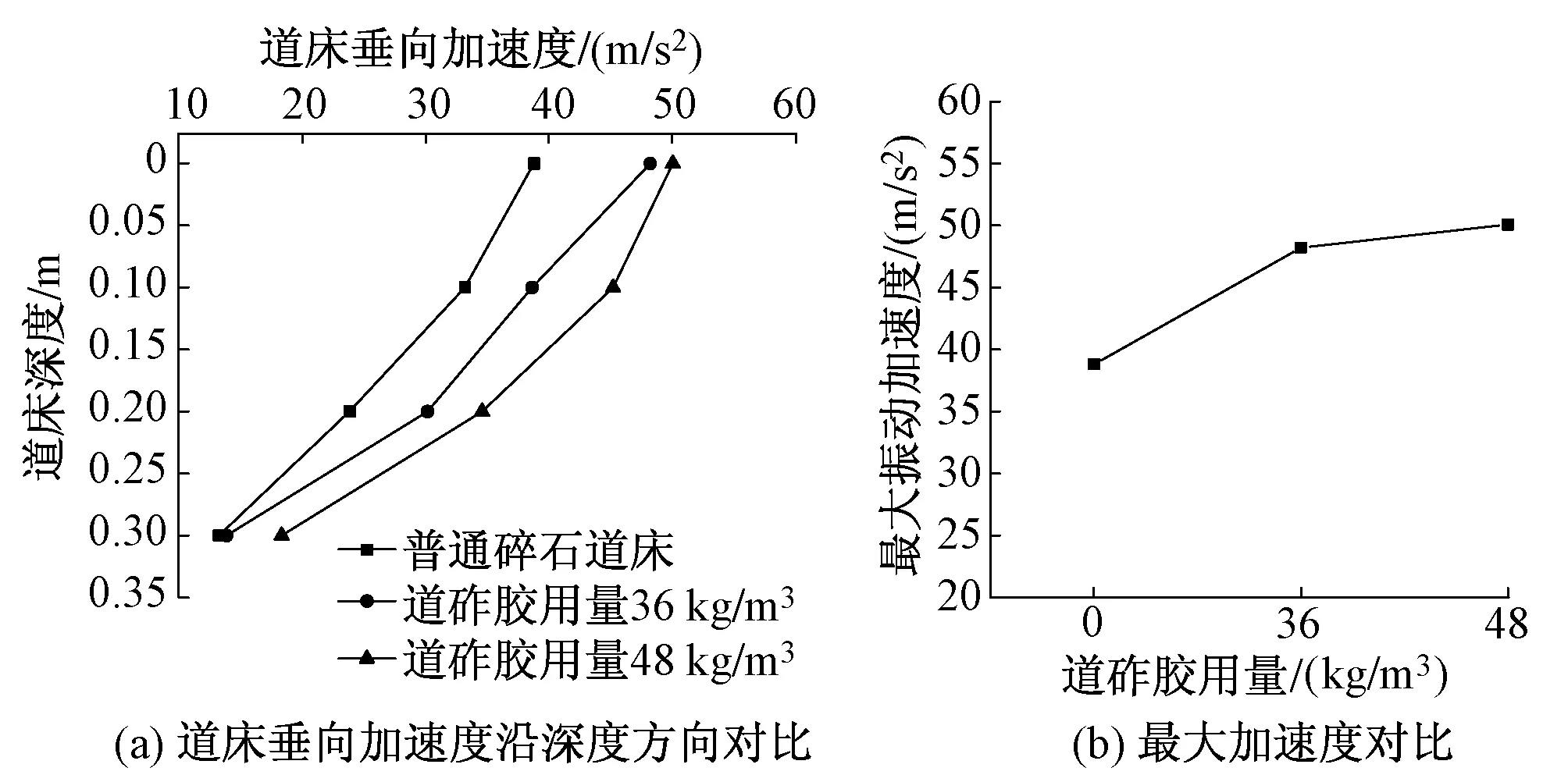
图2 不同道砟胶用量道床加速度对比分析曲线
图2为不同道砟胶用量道床加速度对比分析曲线,可知,随着道砟胶用量的不断增加,整体道床的垂向加速度不断增加,最大加速度也不断增加;沿深度方向,道床的垂向加速度呈现衰减的趋势。普通碎石道床的最大垂向加速度为38.80 m/s2;道砟胶用量36 kg/m3道床的最大垂向加速度为48.21 m/s2,相对于普通碎石道床,增大了24.25%;道砟胶用量48 kg/m3道床的最大垂向加速度为50.06 m/s2,相对于普通碎石道床,增大了29.02%。
2)动位移对比分析
图3为不同道砟胶用量道床动位移对比分析曲线,可知,随着道砟胶用量的不断增加,道床的整体动位移不断减小,最大动位移也不断减小;沿深度方向,道床的垂向动位移呈现衰减的趋势。普通碎石道床的最大垂向动位移为1.56 mm;道砟胶用量36 kg/m3道床的最大垂向动位移为1.25 mm,相对于普通碎石道床,减小了19.87%;道砟胶用量48 kg/m3道床的最大垂向动位移1.18 mm,相对于普通碎石道床,减小了24.36%。
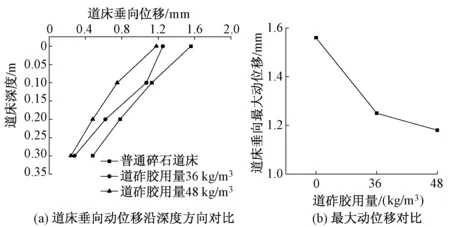
图3 不同道砟胶用量道床动位移对比分析曲线
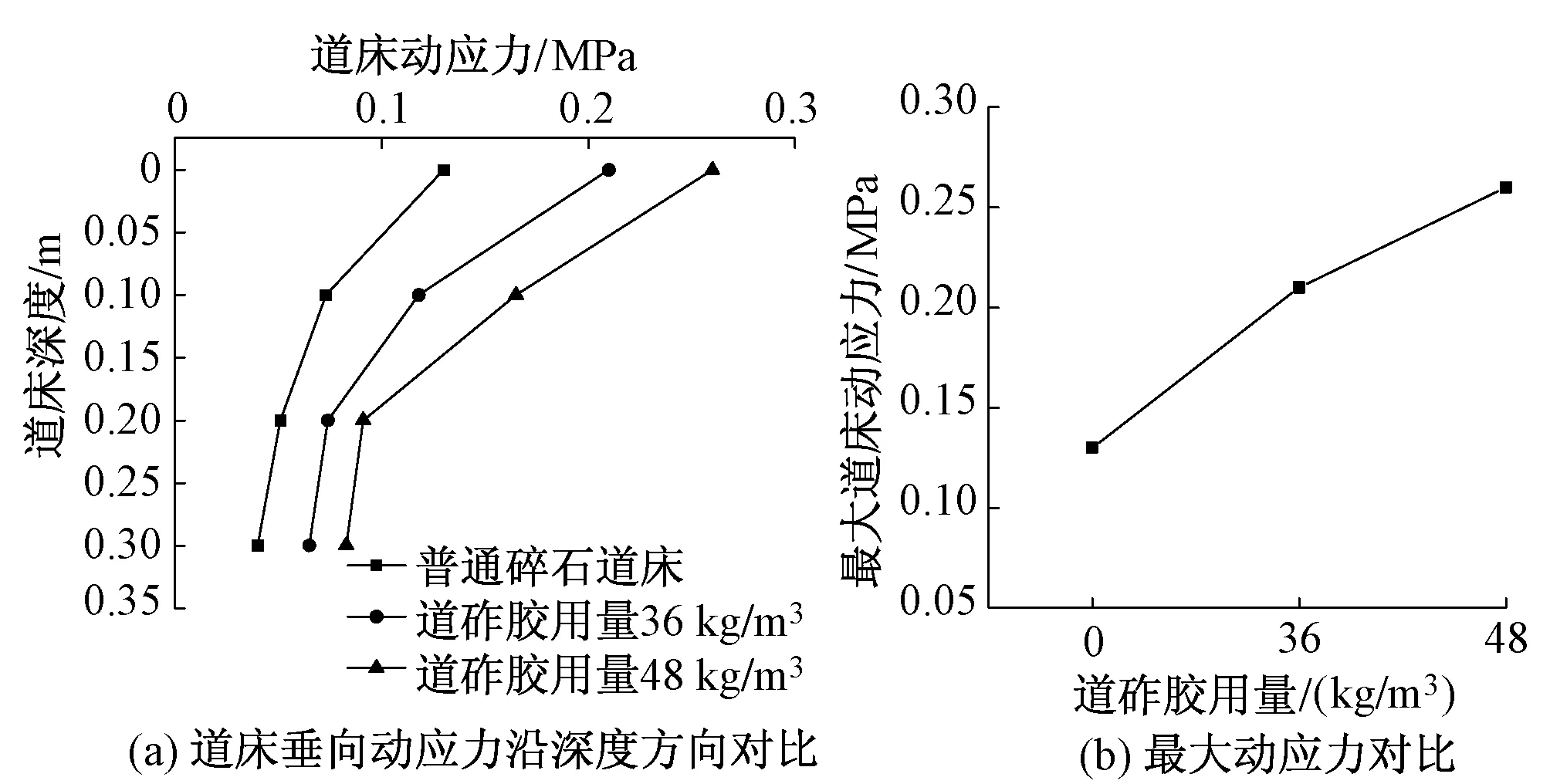
图4 不同道砟胶用量道床动应力对比分析曲线
3)动应力对比分析
图4为不同道砟胶用量道床动应力对比分析曲线,可知,随着道砟胶用量的不断增加,道床的整体动应力水平不断增加,最大动应力也不断增加;沿深度方向,道床的垂向动应力呈现衰减的趋势。普通碎石道床的最大垂向动应力为0.13 MPa,道砟胶用量36 kg/m3道床的最大垂向动应力为0.21 MPa,相对于普通碎石道床,增加了61.54%;道砟胶用量48 kg/m3道床的最大垂向动应力为0.26 MPa,相对于普通碎石道床,增加了100%。
2.2 道砟胶固化深度的影响分析
采用普通碎石道床和道砟胶固化深度0.11,0.22,0.35 m共4种工况进行对比,采用的道砟胶用量均为48 kg/m3,以此来分析道砟胶固化深度对胶粘道砟固化道床的动力学特性的影响规律。
2.2.1 固化深度0.11 m道床的动力学特性
表6为道砟胶固化深度0.11 m道床动力学计算结果,可以看出,道砟胶固化深度0.11 m的道床在实际列车荷载的作用下,最大振动加速度为42.68 m/s2,最大垂向位移为1.38 mm,最大垂向动应力为0.176 MPa,且最大振动加速度、最大垂向动位移和最大垂向动应力位置都在轨枕底面(道床顶面)处。
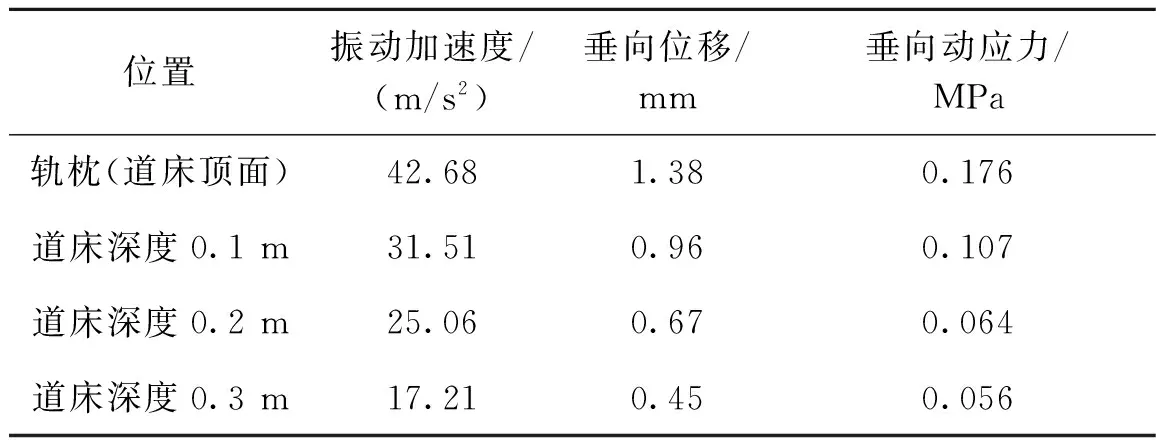
表6 道砟胶固化深度0.11 m道床动力学计算结果
2.2.2 固化深度为0.22 m道床的动力学特性
表7为道砟胶固化深度0.22 m道床动力学计算结果,可以看出,道砟胶固化深度0.22 m的道床在实际列车荷载的作用下,最大的振动加速度为50.13 m/s2,最大垂向位移为1.26 mm,最大垂向动应力为0.213 MPa,且最大振动加速度、最大垂向位移和最大垂向动应力位置都在轨枕底面(道床顶面)处。与道砟胶固化深度0.11 m道床相比,道床沿深度方向整体振动加速度水平有所增加,沿深度方向道床垂向位移有所减小,道床内整体应力水平明显增加,说明随着道砟胶固化深度增加,道床的整体沉降减小,道砟胶的使用能显著减小道床的整体沉降,从而保证轨道结构沿线路方向的平顺性。
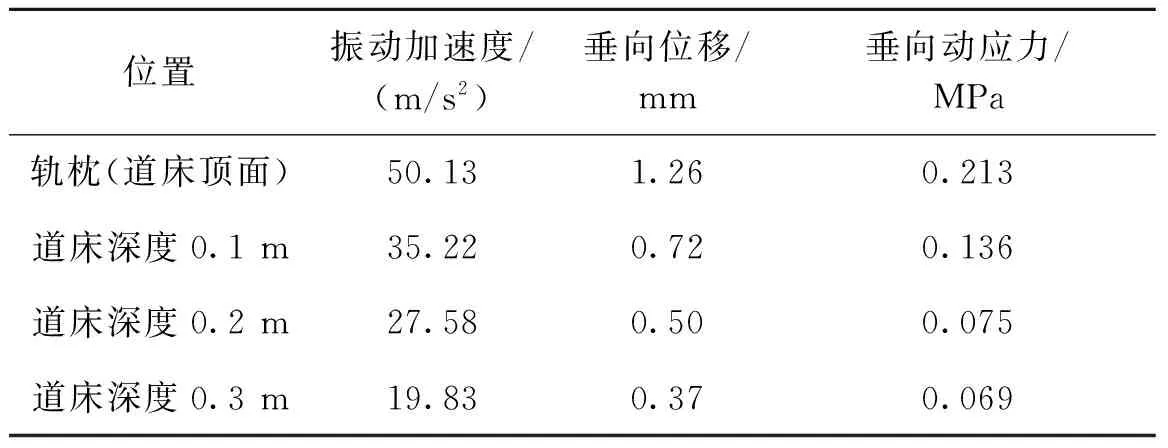
表7 道砟胶固化深度0.22 m道床动力学计算结果
2.2.3 不同固化深度动力学结果对比分析
1)振动加速度对比分析
图5为不同固化深度下振动加速度对比分析曲线。由图5(a)可知,随着道砟胶固化深度的不断增加,整体道床的垂向振动加速度不断增加,由图5(b)可知,从普通碎石道床到道砟胶固化深度0.22 m道床,道床的最大振动加速度不断增加,但是道砟胶的固化深度从0.22 m增加到0.35 m时,最大加速度没有明显变化;沿道床深度方向,道床的垂向加速度呈现衰减的趋势。普通碎石道床的最大垂向加速度为38.80 m/s2,道砟胶固化深度0.11 m道床的最大垂向加速度为42.68 m/s2,相对于普通碎石道床增大了10.00%;道砟胶固化深度0.22 m道床的最大垂向加速度为50.13 m/s2,相对于普通碎石道床增大了29.2%;道砟胶固化深度0.35 m道床的最大垂向加速度为50.06 m/s2,相对于普通碎石道床增大了29.02%。
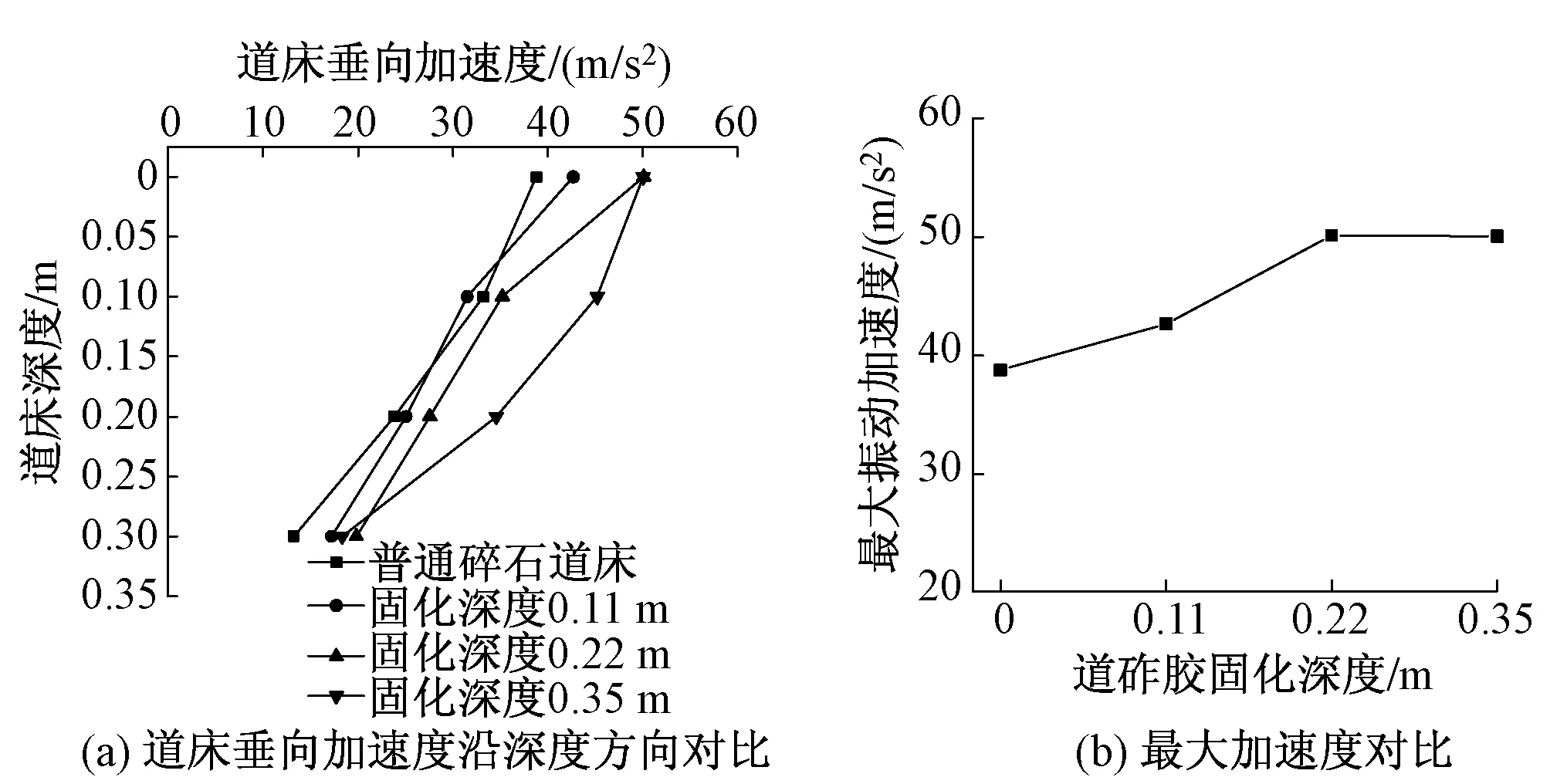
图5 不同固化深度下振动加速度对比分析曲线
2)垂向位移对比分析
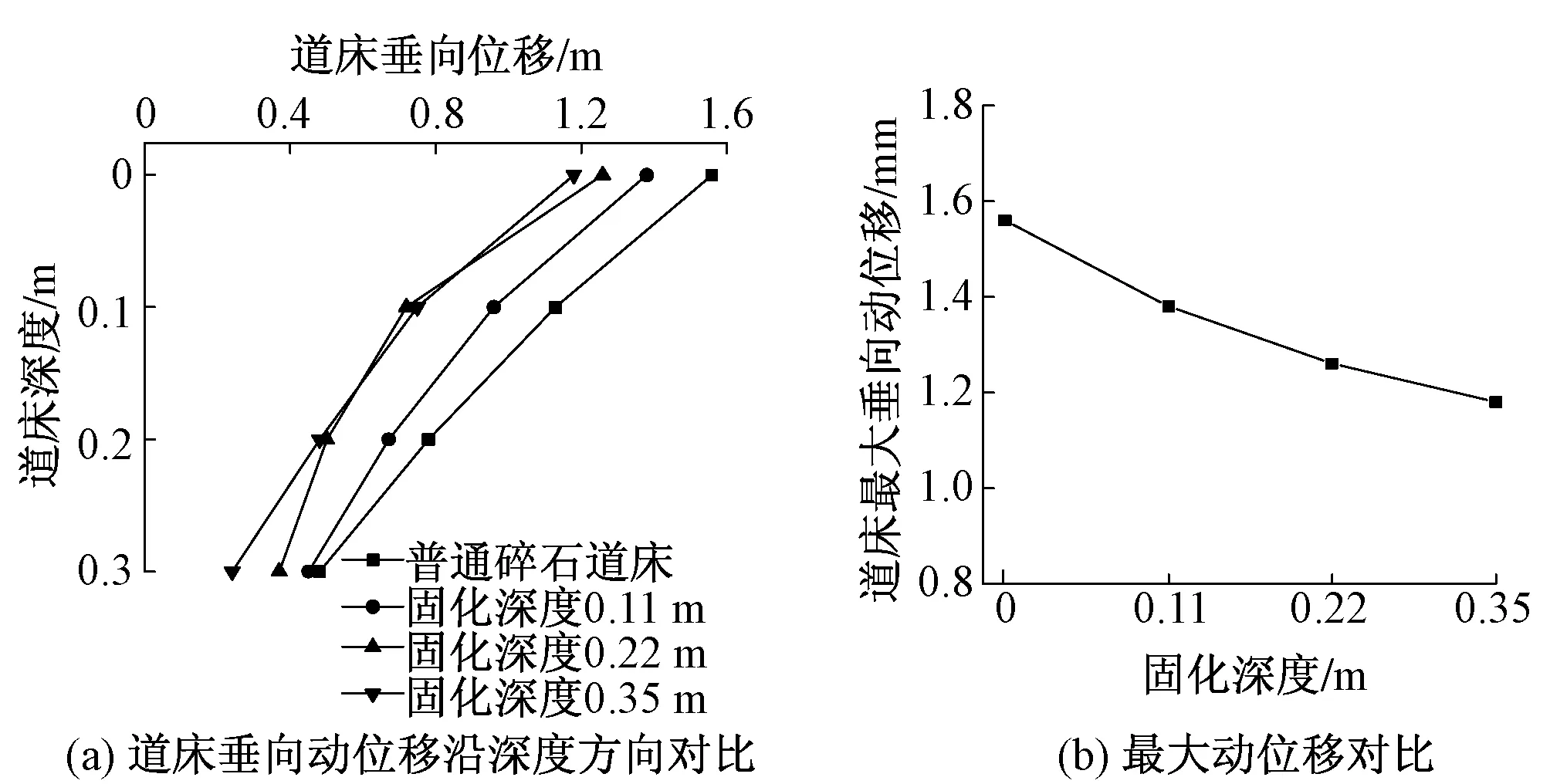
图6 不同固化深度下垂向位移对比分析曲线
图6为不同固化深度下垂向位移对比分析曲线,由图6(a)可知,随着道砟胶固化深度的不断增加,道床的整体位移不断减小;由图6(b)可知,随着道砟胶固化深度增加,道床最大垂向位移也不断减小;沿深度方向,道床的垂向位移呈现衰减的趋势。与加速度情况不同,道砟胶在固化深度达到0.35 m时仍对道床的垂向位移存在影响。普通碎石道床的最大垂向位移为1.56 mm;道砟胶固化深度0.11 m道床的最大垂向位移为1.38 mm,相对于普通碎石道床减小了11.54%;道砟胶固化深度0.22 m道床的最大垂向位移1.26 mm,相对于普通碎石道床减小了19.23%;道砟胶固化深度0.35 m道床的最大垂向位移1.18 mm,相对于普通碎石道床减小了24.36%。
3)动应力对比分析
图7为不同固化深度下道床动应力对比分析曲线,可知,随着道砟胶固化深度不断加深,道床整体动应力水平不断增加,最大动应力也不断增加;沿深度方向,道床动应力呈现衰减的趋势。普通碎石道床的最大动应力为0.130 MPa,道砟胶固化深度0.11 m道床的最大动应力为0.176 MPa,相对于普通碎石道床增加了35.38%;道砟胶固化深度0.22 m道床的最大动应力为0.213 MPa,相对于普通碎石道床增加了63.84%;道砟胶固化深度0.35 m道床的最大动应力为0.26 MPa,相对于普通碎石道床增加了100%。
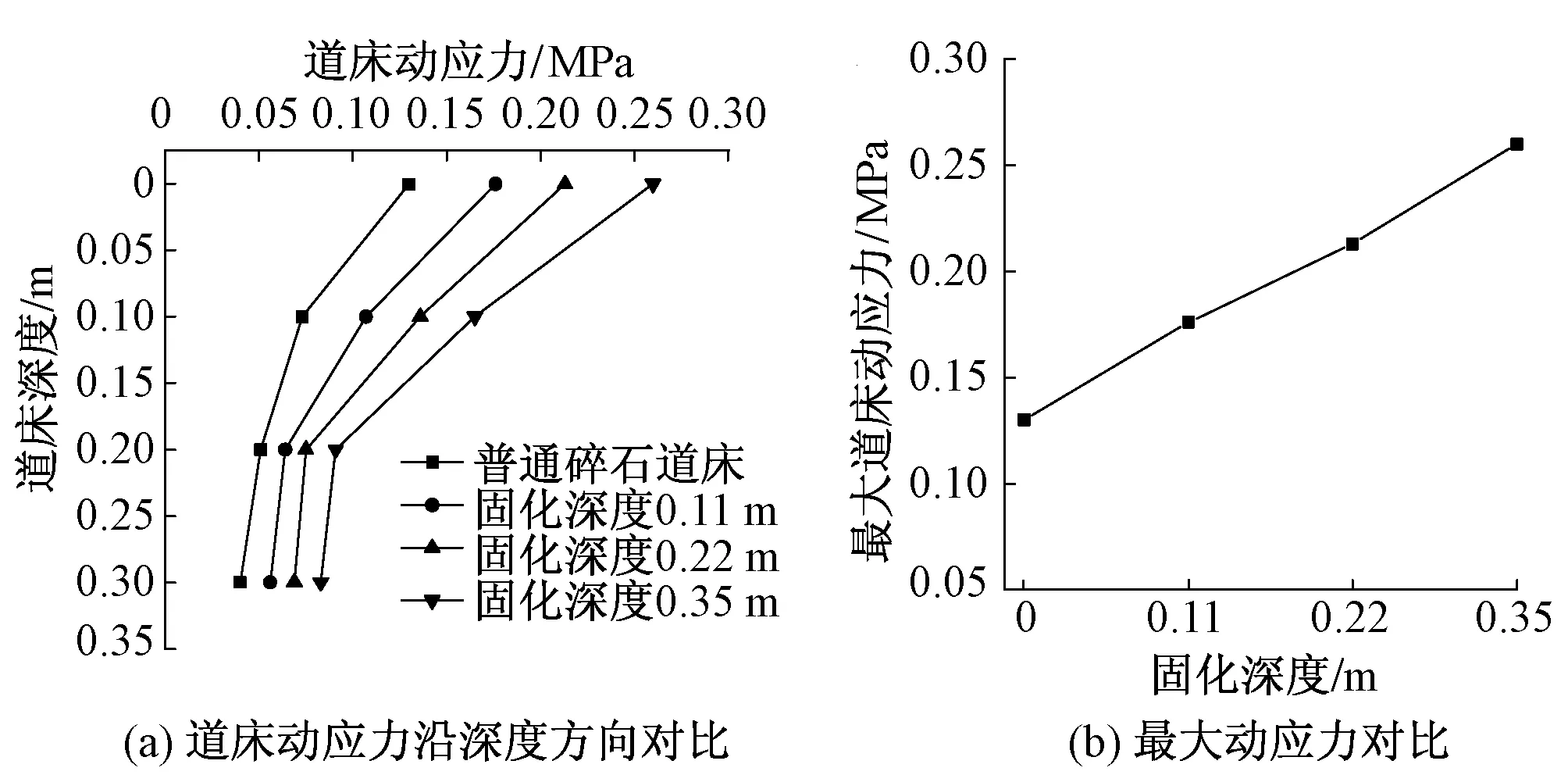
图7 不同固化深度下道床动应力对比分析曲线
3 结论
本文利用有限元软件ABAQUS建立车辆-轨道结构空间耦合模型,从道砟胶用量和道砟胶固化深度2个因素来分析道砟胶对道床动力学特性的影响,总结道砟胶用量和固化深度的变化对轨道结构的受力变形、振动特性的影响规律。得到以下结论:
1)通过对比分析不同道砟胶用量和道砟胶固化深度对散体道床动力学特性的影响规律,可以发现,随着道砟胶用量的增加和道砟胶固化深度的加深,道床内的振动加速度水平显著提升,道床的动位移水平明显降低,证明道砟胶的使用能够保持轨道几何形位,减少轨枕和道床的沉降,有效提高普通道砟的刚度。通过合理选用道砟胶的用量和道砟胶固化深度,可以实现无砟轨道-有砟轨道结构刚度平稳过渡,对提高列车行驶平顺性和舒适性,具有实际意义。
2)随着道砟胶用量和道砟胶固化深度的加深,道床内的整体应力水平显著提升,证明采用道砟胶将道床黏结成一个整体,可均化道床受力,且随着道砟胶用量和固化深度的增加,应力衰减效果越显著。
[1]LIM W L,MCDOWELL G R.Discrete Element Modelling of Railway Ballast[J].Granular Matter,2005,7(1):19-29.
[2]RICCI L,NGUYEN V H,SAB K,et al.Dynamic Behaviour of Ballasted Railway Tracks: A Discrete/continuous Approach[J].Computers and Structures,2005,83(28):2282-2292.
[3]王浩宇.高速铁路无砟有砟过渡段优化设计[D].北京:北京交通大学,2012.
[4]王平,万复光.铁路碎石道床弹性特性研究初探[J].铁道学报,1997,19(4):109-115.
[5]郭积程.高速铁路路基上有砟轨道与无砟轨道过渡段研究[D].北京:北京交通大学,2009.
[6]王红.铁路有砟道床聚氨酯固化技术的发展及应用[J].铁道建筑,2015,55(4):135-140.
[7]贾璐.高速车辆动力学性能评价方法研究[D].成都:西南交通大学,2011.
[8]雷晓燕.列车通过轨道不平顺和刚度突变时对轨道振动的影响[J],铁道科学与工程学报,2005,2(6):1-8.
[9]朱永见,亓伟,陈攀.道砟胶对过渡段道床参数的影响规律研究[J].铁道科学与工程学报,2016,13(1):34-39.
[10]罗强,蔡英.高速铁路路桥过渡段技术处理措施的研究[J].铁道工程学报,1999,16(3):30-33.

