一类分数阶 SEIS 模型的稳定性分析
,
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
传染病历来是危害人类身体健康的大敌,从古至今传染病传播给人类的生存和国际民生都带来了巨大的灾难[1-2]。定量或定性的研究传染病传播的机制可以为预防和控制疾病提供重要的基础。
文献[3-5]研究了一类整数阶SIS(susceptible-infective-susceptible)传染病模型,讨论了平衡点的稳定性。对于一些具有潜伏期的传染病,像流感、狂犬病等,应考虑潜伏性,因此有必要研究SEIS(susceptible-exposed-infective-susceptible) 传染病模型[6-7]。文献[7]分析了整数阶SEIR(susceptible-exposed-infective-recovery)模型的稳定性并提出了SEIS模型。文献[8]提出了一种考虑治疗的新型SEIS模型的活动患者和潜在患者,文献[9]对此模型的稳定性进行了分析。然而上述文献均没有考虑模型为分数阶的情形。
分数阶微积分是微积分的一个分支,主要研究任意阶积分和导数的理论及其应用,最早是于 1695 年由 Leiblilz 和 L’Hospital提出。分数阶微积分作为整数阶微积分的一种推广,是伴随整数阶微积分的发展而产生的,已有 300 多年的历史。目前传染病模型绝大多数是用常微分方程组、差分方程组、偏微分方程组或时滞微分积分方程组描述的,所涉及到的方程阶数均为整数阶。整数阶导数具有局部性,不适合描述具有历史依赖的过程模型;分数阶导数具有全局相关性,能较好地体现系统函数发展的历史依赖过程[10-12]。基于以上分析,将分数阶引入到传染病建模具有非常重要的现实意义。
文献[13]分析了如下分数阶SIS模型的平衡点的稳定性,得出该模型的平衡点在α=1,0.9,0.8时都是稳定的。
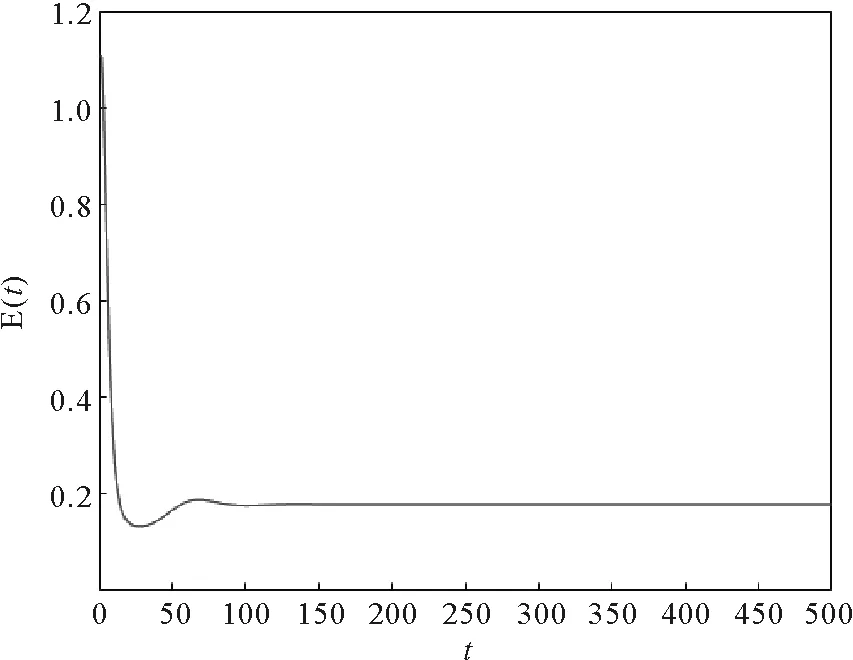
其中:0 文献[14]提出了如下不考虑治疗的分数阶SIR模型并对模型的平衡点的稳定性进行了分析,得出模型地方病平衡点和无病平衡点都是局部渐进稳定的,并且具有唯一的一致李雅普诺夫稳态正解。 其中R代表康复者的数量,其余的参数同上。作者进一步考虑了具有治疗的分数阶SIR流行病模型,提出模型: 并对模型的平衡点稳定性进行了分析,得到了后向分支发生的条件。 结合文献[9]中的SEIS模型,本文提出如下分数阶SEIS模型: (1) 下面将证明该模型平衡点的存在唯一性,分析其无病平衡点和地方病平衡点的局部稳定性和全局稳定性;并通过数值仿真验证其理论分析的正确性。 定义1[15]函数f(t)的Caputo分数阶微积分的定义为: 其中Γ(.)是伽马函数,n-1 引理1[16]考虑具有Caputo分数阶导数的非线性微分方程 DaX(t)=f(X(t))。 (2) 引理2[17]假设f(t)∈C[a,b]且Daf(t)∈C[a,b],a∈(0,1]。若Daf(t)≥0,∀t∈[a,b],则对每个t∈[a,b],f(t)是非减函数;若Daf(t)≤0,∀t∈[a,b],则对每个t∈[a,b],f(t)是非增函数。 引理3[17]假设向量函数f(t,x):R+×Rn→Rn(维数n≥1)满足 1)f(t,x)在R+上关于t是Lebesgue可测的; 2)f(t,x)在Rn上关于x是连续的; 的解x(t)在R+上存在且唯一。 定义2[18]设Ω是Rn中的一个开子集,考虑下面的自治系统 Rn=f(x),f(0)=0。 (3) 若V(x)∈C1(Ω,Rn),则V(x)沿着方程(3)解的α阶导数为 引理4[18](分数阶系统LaSalle不变原理)设D是下列系统的一个正不变集,若∃V(x):D→R,具有连续一阶偏导数,使 DαV|(3)≤0。 又设E={x|DαV|=0,x∈D},M⊂E是最大不变集,则当t→+∞时,有x(t,t0,x0)→M,特别地,若M={0},则系统的平凡解是吸引的。 证明: 首先,说明系统存在唯一解。根据引理3,系统的向量函数为 显然,f满足引理3的1),2),4)三个条件,为了证明系统(1)解的存在唯一性,只需证明向量函数f满足引理3中的条件3)。 令x1(t)=S(t),x2(t)=E(t),x3(t)=I(t),x(t)=[x1(t),x2(t),x3(t)]T,μ=[A,0,0]T, 则系统方程可以简写为: Dαx(t)=A1x(t)+A2x(t)x3(t)+η 则: 其次,证明系统(1)解的非负性,由系统(1)得 将系统(1)的3个方程相加并变形得: DαN=A-μ(S+E+I)=A-μN, 其中N=S+E+I, 定理2如果0 证明:当无病毒感染(I=0)时,系统(1)始终存在一个无病平衡点 且在无病平衡点E0处的雅可比矩阵为: 特征方程为: 整理得 系统(1)的无病平衡点E0的稳定性取决于特征方程的根位置。 当方程的所有根位于复平面的左半平面,则无病平衡点E0稳定。 易知一个特征根λ1=-μ,那么只需要讨论下面的等式 计算可得 (4) 根据韦达定理可得 (5) 可得 (β+r1+μ)(μr2+μ2-αpA)-β(1-p)αA>0。 推出 (6) 容易得到 Reλ2<0,Reλ3<0, 又有 λ1=-μ。 因此,当0 定理3如果R0>1,地方病平衡点E1(S*,E*,I*)是局部稳定的。 证明:设E1(S*,E*,I*)为地方病平衡点,则有 (7) 解得 系统(1)在E1(S*,E*,I*)处的雅可比矩阵为: 其特征方程为: 注意到,当λ=-μ时特征方程等于0,即: (8) 容易得到存在一个特征根 λ=-μ。 (9) 令λi(i=1,2,3)是矩阵J(E1)的特征值;可以假设λ1=-μ特征方程可以重写为: (λ+μ)[λ2+(2μ+r1+r2+β-pαS*+αI*)λ+(r2+μ)(1-p)αI* +(r2+μ)pαI*+(r1+μ)pαI*+βαI*]=0。 (10) 只需考虑: λ2+(2μ+r1+r2+β-pαS*+αI*)λ+(r2+μ)(1-p)αI* +(r2+μ)pαI*+(r1+μ)pαI*+βαI*=0 。 (11) 由韦达定理可得 λ2+λ3=(pαS*-r2-μ)-μ-β-αI*-r1 λ2λ3=(r2+μ)(1-p)αI*+(r1+μ)pαI*+βαI*>0。 容易得到 Reλ2<0,Reλ3<0, (12) 又有λ1=-μ<0。因此Reλi<0(i=1,2,3),所以E1是局部稳定的。证毕。 定理4如果0 证明:令 V(t)=βE(t)+(β+r1+μ)I(t) (13) 则V沿着系统(1)的解的α阶导数为 DαV|(1)=I1-αDV|(1) =(β(1-p)αS(t)+(β+r1+μ)pαS(t) -(β+r1+μ)(r2+μ)I(t) (14) 若R0<1,可以得到 (15) 由V(t)=βE(t)+(β+r1+μ)I(t)和β+r1+μ>0可得 (16) 其中V(0)=βE(0)+(β+r1+μ)I(0)。 由R0<1可得 因此可得 当R0>1时,存在正数ε,使得 β(1-p)α≥(β+r1+μ)(r2μ+μ2+pαA)+ε。 (17) 根据DαV|(1)=(β(1-p)αS(t)+(β+r1+μ)pαS(t)-(β+r1+μ)(r2+μ)I(t)得: (18) 从该地区开始的系统(1)的解 (19) 远离E0。证毕。 模型参数取为:a=0.99,A=0.3,α=0.7,β=1,p=0.4,μ=0.5,r1=0.1,r2=0.1,S(0)=3,E(0)=1,I(0)=2。 经计算可得R0≈0.364 6<1。根据定理4可得无病平衡点是全局渐近稳定的。仿真结果见图1~3。 基于上述假设参数值集,选择A=0.6,可得R0=1.19>1。仿真结果见图4~6,由仿真可见系统(1)的地方病平衡点是局部稳定的。 图1 R0<1的系统(1)的S(t)的时间序列Fig.1 Time series of S(t) of the system (1) for R0<1 图2 R0<1的系统(1)的E(t)的时间序列Fig.2 Time series of E(t) of the system (1) for R0<1 图3 R0<1的系统(1)的I(t)的时间序列Fig.3 Time series of I(t) of the system (1) for R0<1 图4 R0>1的系统(1)的S(t)的时间序列Fig.4 Time series of S(t) of the system (1) for R0>1 图5 R0>1的系统(1)的E(t)的时间序列Fig.5 Time series of E(t) of the system (1) for R0>1 图6 R0>1的系统(1)的I(t)的时间序列Fig.6 Time series of I(t) of the system (1) for R0>1 主要研究了一类分数阶SEIS传染病模型的无病平衡点和地方病平衡点的稳定性。利用特征根方法得出:当0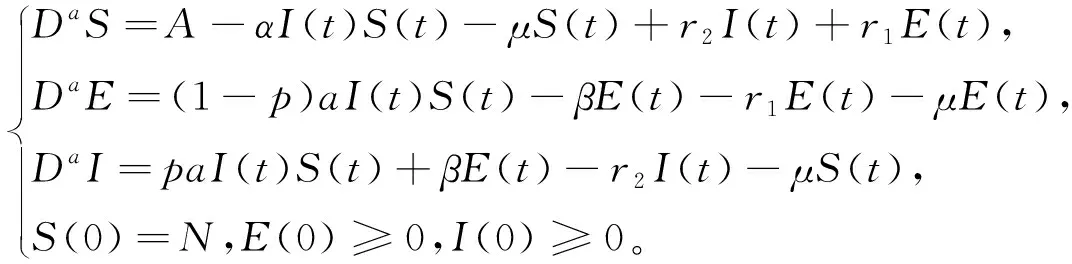

1 基础知识



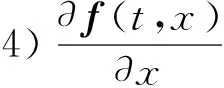

2 平衡点及其稳定性
















3 数值仿真





4 结论

