基于粒子系统的矿井突水蔓延仿真研究

,

(山东科技大学 电子通信与物理学院，山东 青岛266590)

矿井突水灾害是煤矿的主要灾害之一[1]，矿井突水造成淹井和伤亡事故，给国家、社会和家庭带来严重的直接或间接的经济损失和人身损害。因此，矿井突水蔓延研究对矿井治水安全具有重要意义。张丽娟[2]研究了基于OSG的矿井突水应急虚拟仿真系统关键技术，改进MC和光滑流体动力学(smoothed particle hydrodynamics，SPH)算法，基于表面纹理和粒子系统完成了水灾的真实感表达。刘欣倩[3]研究了基于Unity 3D粒子系统进行矿井突水事故的虚拟仿真，展示了突水淹没巷道的情景。李长春[4]进行了巷道建模和水淹模拟,宏观展现水淹巷道情景，但缺乏水灾蔓延动态研究。李翠平等[5]结合水灾流动的水力特征，建立了能够真实模拟水流蔓延三维动态仿真模型，但只是宏观体现。汪金花等[6]、王鹏[7]进行了水灾仿真实验，主要研究的是水灾数学模型和最优避难路径。赵怡晴等[8]构建了矿井突水仿真的一体化模型，宏观展示了水灾淹没范围。

对于虚拟环境中矿井突水灾害逃生培训来说，巷道内突水蔓延的动态模拟能够为安全训练提供较好的辅助作用，因此对水体本身进行具有物理规律的真实感模拟是突水蔓延模拟的需求。基于物理的流体模拟方法分为基于网格的欧拉法和基于粒子的拉格朗日法。用欧拉网格法模拟流体的计算效率较高，Stam[9]提出基于网格法的流体模拟，提高了流体的稳定性和计算效率。邵绪强等[10]提出一种基于shallow water方程的物理模拟方法，加速大规模流体的物理模拟计算。1983年，Reeves[11]首次提出了粒子系统的方法并广泛应用到虚拟仿真中。Hu等[12]基于SPH算法在游戏引擎使用粒子系统进行了流体的模拟。基于粒子的拉格朗日法特别是SPH粒子法能够避免欧拉方法网格扭曲的缺陷而且能够处理流体自由边界问题，适合求解高速碰撞等问题[13-14]。

本研究采用SPH算法求解N-S方程获得流体的物理模型并应用到粒子系统，采用固定边界粒子法进行边界处理，结合三维八叉树方法进行表面重构实现水体的渲染，在Unreal Engine 4中实现了水流体的运动仿真效果，并在三维巷道地形中实现了突水水平流动、上向升涨和下向蔓延的仿真。使得沉浸性和交互性的矿井水灾逃生培训和灾情预测成为可能，在矿井突水灾害逃生演习中起到重要作用。

1 SPH数值解算

光滑粒子流体动力学，是一种基于物理的纯拉格朗日粒子算法[15]。在SPH方法中，将流体视为质点系，系统的状态用包含各种物理量(密度、压力、速度等)的质点来描述，通过求解质点组的动力学方程和跟踪每个质点的运动轨道，求得整个系统的力学行为。SPH的公式构造不受粒子分布的随意性影响，可以很自然地处理一些具有极大变形的模拟情况[16]，适用于矿井水灾蔓延模拟的研究。

基于粒子的流体模拟中，每个粒子的运动都遵循牛顿第二定律：F=ma。在SPH方法中，流体粒子的质量取决于粒子的密度，所以一般用密度来代替质量。作用在粒子上的力由外力、压力和粘性力组成。因此水作为一种不可压缩粘性流体，其模拟可用以下N-S方程的简化形式描述：

ρa=-p+ρg+μ2u。

(1)

其中：ρ为液体的密度，p为压力，u为速度，为梯度，μ为粘性系数，2为拉普拉斯算子。忽略其他相关较小的力，外部力一般指重力，外力F=ρg。μ2u表示粘力项。

假设流体中一个位置为ri的点，此处的密度为ρ(ri)、压力为p(ri)、速度为u(ri)，那么根据公式(1)，可以计算出此处粒子的加速度

(2)

采用跳蛙(leap-frog)算法对加速度进行时间积分后，得到粒子在下一时刻的速度与位置[17]。在半个积分时间步得到速度，并利用这一速度计算新的位置，其位置和速度表达式为：

(3)

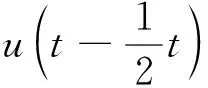
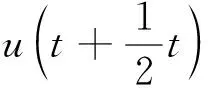
(4)

SPH方法中，整个系统是由具有独立质量、占有独立空间的有限个粒子表示的。可以由以下粒子近似法得到。假设流体中某点r(此处不一定有粒子)，在光滑核半径h范围内有数个粒子，则该处场量A的计算可近似为：

(5)

其中，Ai指的是要累加的某种场量，本研究的场量是外力、密度、粘度；r指的是该粒子的当前位置，ri为i处的粒子位置；h指的是光滑核半径；函数W是光滑核函数。

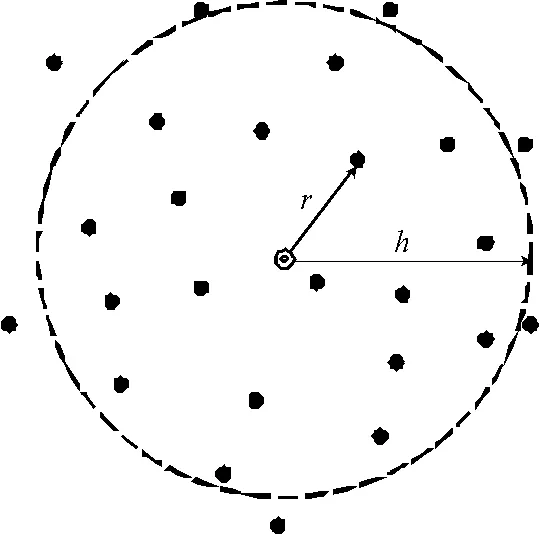
图1 光滑函数影响阈内的粒子示意图Fig.1 Schematic diagram of the particle in the threshold of the influence of smooth function

本研究在SPH方法的基础上进行流体模拟，通过SPH算法将流体连续方程转化为支持域内粒子求和的离散方程，其压力项和粘力项的求解式分别表示为：

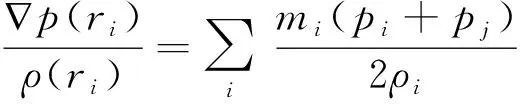
(6)

(7)

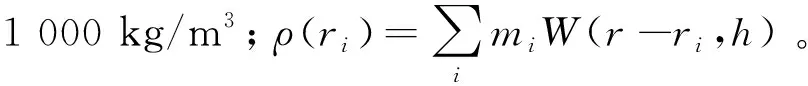
对于密度项选取的光滑核函数为：

(8)

对于压力项选取的光滑核函数为：

(9)

对于粘力项所用的光滑核函数选取

(10)

由式(2)，式(5)～(10)即可求出粒子的加速度，进而根据式(3)、(4)获取粒子下一时刻的速度与位置。

2 边界处理

基于SPH的粒子法是纯拉格朗日粒子方法，粒子与边界的作用力必须转化为粒子与粒子之间的相互作用才可以进行计算。本研究采用一种精确并节省时间的固定边界粒子法[20]，将粒子与边界的作用转化为粒子与粒子之间的作用，得以应用SPH方法计算边界问题。

如图2所示，固定边界粒子法在边界上布置固定粒子，用边界粒子与流体粒子反应代替固体边界与流体粒子发生反应，通过内部粒子的压力，估计边界粒子的压力。

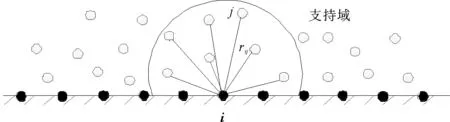
图2 固定边界粒子法Fig.2 Fixed boundary particle method

选取以光滑长度h为半径的区域所有内部流体粒子，然后计算内部流体粒子与边界粒子的间距rij，再通过式(11)近似求得此处的压力

(11)

式中，rij表示边界粒子i支持域内的粒子j到边界粒子i的距离，Pi表示粒子i的压力，h表示光滑长度。通过公式可以看出，距离边界点较远的粒子，h-rij较小，其对边界点的压力贡献值较小；反之，距离边界点越近，h-rij较大，对Pi的影响越大。求得Pi后，在求解i粒子的受力时，Pi会对i产生影响，通过这种方式保证了粒子不会超出固壁边界，符合正常的物理规律，模拟出的粒子边界效果更为真实。计算过程中，边界粒子和内部粒子一样，搜索临近粒子，计算压力和密度，不同的是边界处的粒子速度始终为零，即粒子不发生运动。

3 流体渲染

流体效果的渲染基于八叉树的自适应流体的表面重建方法[21]，跟踪流体表面的粒子，构建自适应距离场。对于任意流体的粒子i,计算一个再归一化矩阵Bi[22]:

Bi=[∑jW(ri)⊗(rj-ri)Vj]-1。

(12)

图3 渲染流程Fig.3 Rendering process

(13)

然后根据八叉树结点对不同粒子间距采样，构建自适应距离场，重建出仅由一层粒子构成的薄膜结构的网格表面用于流体表面绘制。再结合Unreal Engine 4的shader着色程序进行最终的渲染。

Unreal Engine 4中，纹理(Texture)是基于GPU上需要运用特定的数据结构，纹理的坐标、纹理的查询分别相当于数组中元素的索引和元素的读取。

首先，把距离场的FDistanceFieldVolumeTexture数据对应提交到GPU中的3D纹理DistanceFieldTexture中；随后，通过调用函数使流体的距离场数据与全局距离场的网格相对应，此时需要变换矩阵使GPU距离场的数据与世界空间的数据相互转化；最后针对每一个视口网格生成一个全局距离场大小相同、密度不同的3DTexture，并在此网格进行更新。

以上步骤完成后，需要将所有数据渲染到当前相机的平面，呈现在屏幕。根据摄像机坐标系下的坐标值，可以求得在当前摄像机下最近点的三维坐标，将屏幕作为投影平面，相机的中点作为起点，向模型距离场发出的采样射线与场景中的流体表面相交，计算出此交点的属性，就获取流体距离场中每个网格的属性数据，纹理采样然后进行绘制。绘制之前启用深度缓冲(Depth Buffer)对比采样点的距离生成正确的深度感知效果。最后调用一个DrawRectangle把距离场信息贴到对应的View全屏上。

流体表面绘制自定义函数如下：

void WaterShaderOnSurface(float4 surfPos)

{

float3 surfNorm = CalcSurfaceGrad(surfPos.xyz);

float3 WorldPosition = GetWorldPosition(surfPos.xyz);

float FluidDist =(surfPos.w - lastPos.w) * WorldRayDirLen;

float3 WorldNormal = normalize(surfNorm);

WaterShader.OnEnterSurface(lastPos.xyz+surfPos.xyz)*0.5f, FluidDist);

}

4 水灾仿真实验

在进行矿井突水蔓延仿真实验时选择的验证平台为：硬件平台为Intel Core i7-7700 CPU @3.60 GHz处理器、16 GB内存、NVIDIA Titan XP显卡；软件平台为Windows 10操作系统，仿真平台为Unreal Engine4和Visual Studio 2015。

在Unreal Engine 4源代码中定义解算相关函数，通过解算获得粒子的速度、位置等参数；然后在Unreal Engine 4编辑器中创建粒子Particle蓝图类，修改粒子的数量、周期和颜色等参数。

在巷道中，流体的边界主要是与巷道墙壁和设备的交界面，把巷道壁和巷道内设备作为刚体处理，从Unreal Engine 4距离场数据的3D纹理中获取边界信息后，在边界上布置一层固定粒子，利用粒子与边界粒子间的作用计算粒子在边界处与墙体碰撞后的流动状态。

生成固定边界粒子的部分函数如下：

Void BuildSBoundaryParticle(uint3DispatchThreadId:SV_DispatchThreadID)

{uint3 ijk = GetActiveIndex(DispatchThreadId);

float DistanceToNearestSurfaceParticle;

}

计算粒子下一刻的速度函数：

Velocity.xyz += DiffuseParticles.DeltaSeconds * acc.xyz /2* 100

得到粒子更新的速度，相应位置确定为：

Position.xyz += DiffuseParticles.DeltaSeconds * Velocity.xyz。

4.1 突水蔓延效果展示

在Unreal Engine 4中用画刷工具绘制实验所需的矿井巷道三维模型，进行突水蔓延模拟的巷道模型部分结构如下：

1) 将最终构建完善的粒子系统作为一个Actor加入到巷道模型中的突水位置；

2) 主要参数值设置为：

Spawn.Rate.Constanat=40 000.0;

图4 巷道部分结构图

Spawn.Rate Scale.Constanat=2.0;

LifeTime.Constant=1 000.0;

Start Velocity =(100.0,0.0,0.0)。

实验中，最先发射出的粒子在落到巷道表面时重力与边界粒子的支持力相互抵消，只有后面的粒子对其施加一个压力产生加速度向前，其他粒子由压力、重力和粘性力共同产生加速度，由SPH水模型的求解流程获得粒子下一刻的速度与位置，表现出水流向前蔓延的效果。

突水下向蔓延过程中，重力、粘力、压力的合力提供给水流沿巷道地表面的加速度，表现出水流沿斜面向下的流动状态。突水上向蔓延过程中，水流持续蔓延至巷道低洼处，每个粒子占据一定的空间体积，底部粒子不断地往上层累积，水面不断抬高。

当突水蔓延过程发生在巷道左侧分叉口，由于左侧墙壁不再有粒子对流体产生压力，左侧流体表面粒子只受到内部相邻流体粒子向左的压力，上部的流体粒子受自身重力和相邻内部流体粒子的压力，部分粒子会产生向左的加速度，因此产生流体在分叉口分流的现象。

最终部分巷道内突水蔓延仿真效果如图5所示，其中右侧黑色+标记处为突水点。通过仿真的实验结果可以看到，在突水发生后，水流首先涌入低洼处平坦地势的巷道进行下向蔓延，在水流灌满低洼处巷道后水位开始上涨，随后水流会沿地势由低到高灌满整个巷道，并在分叉处分流。

图5 巷道突水蔓延效果Fig.5 Simulation results of water inrush in roadway

本研究的方法在Unreal Engine 4虚拟环境中实现了突水蔓延的状态，巷道内部蔓延效果图如图6所示，在具有真实感的突水仿真的同时，实现蔓延的动态变化趋势。效果直观可见，相对于其他路径算法研究的突水蔓延，具有客观的实用性。

图6 巷道内部蔓延效果图Fig.6 Effect of internal spread of roadway

5 结论

运用SPH算法求解粒子的压力项、密度项和粘力项得到粒子的加速度最终求得粒子的速度与位置，最终在复杂地形的巷道中实现了具有真实物理规律的突水蔓延仿真，包括水流上向蔓延、水流下向蔓延和水流在交叉口处的蔓延状态。通过实验，所研究的突水蔓延可以应用于矿井水灾逃生模拟中，但本研究的突水蔓延仿真局限于较小的巷道范围，下一步需要对大型巷道蔓延进行研究。