三能级Λ型原子系统中边频对相位调制光栅的影响

, , ,

(1.上海理工大学 上海出版印刷高等专科学校，上海200093；2.南阳师范学院 物理与电子工程学院，河南 南阳 473061)

一直以来，原子相干效应引起学术界广泛兴趣，电磁诱导透明[1-2]是其中最为有趣的光学现象之一。基于电磁诱导透明，1998年Ling等[3]首次提出电磁感应光栅的概念。在一个三能级∧型原子系统中，两个能级跃迁分别与一个强的相干泵浦场和一个弱的探测场耦合作用，干涉相消作用下探测场在介质中变得透明，这个现象被称为电磁感应透明。当其中的强相干泵浦场被一个驻波场所替代时，会出现探测场在泵浦场波幅处透射，而在波节处被吸收的现象。因此，该原子系统行为上就是一个周期性光栅，电磁感应光栅因此而形成。由于在无背景技术[4]、相干布居俘获[5]、光开关[6]、介质光学性质探测[7-9]等方面的许多潜在应用[10-14]，近些年来电磁感应光栅受到广泛关注。肖敏及其合作者通过在双暗态系统中加入微波场提高了相位光栅效率[10]；Araujo[11]提出基于巨Kerr非线性效应的电磁感应光栅方案；王丽等[13]研究了四能级三脚架型原子系统内二维诱导电磁感应光栅；借助自发辐射相干，原子系统内相位光栅效率可以显著提高[14-16]。与此同时，固态介质内电磁感应光栅也相继得到研究[17-20]。在半导体量子点—金属纳米粒子混合系统内[17]，基于激子诱导透明的电磁感应光栅在其中成形；基于Fano干涉，在半导体纳米量子阱中也得到电磁感应光栅[19]。

然而，以上大多是单色光场与介质相互作用的例子。单一频率值的单色光场属于理想状态，相比较而言，以某一频率为中心伴随近共振边频成分的多色场更接近现实。而且已知原子系统内多色相干能够控制吸收色散性质，诱导许多有趣的光学效应[21-26]。受此启发，本研究利用边频相干与干涉效应研究了双色场耦合三能级∧型原子系统中边频对相位调制电磁感应光栅的影响。边频相干使得该结构中电磁感应透明窗口从一个拓展到多个。分析该系统边频存在时的吸收色散性质，选择合适的边频强度，利用边频干涉效应，相位衍射光栅强度尤其是一阶衍射得到增强。与此同时，相位衍射光栅衍射效率也依赖于探测失谐、边频与中心频率之间的频差、相互作用长度等参数。当系统参数调节适当时，一阶衍射强度呈显著增强趋势。

1 基本原理

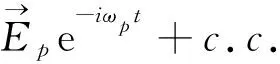
(1)

图1 (a)与弱单色探测场和双色泵浦场相互作用的Λ系统能级图；(b)双色泵浦场和单色探测场在介质中传输Fig.1 (a)Schematic diagram of energy levels for a Λ-system interacting with a weak monochromatic probe field and a bichromatic pump field;(b) Sketch of the bichromatic pump field and the probe field propagating through the sample

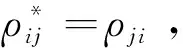
(2)

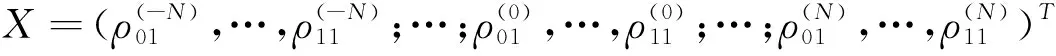
(3)

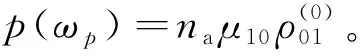
从介质的极化表达式p(ωp)=ε0χEp，我们可以推导出探测极化率为：

(4)

为了获得在介质中传输的探测场的衍射情况，需解麦克斯韦方程。在慢变振幅近似及稳态条件下，关于Ωp的自洽方程为：

(5)

通过解此方程得到作用长度为L的介质中的传输函数

T(x)=eiχL=e-lm[χ]LeiΦ，

(6)

其中相位

Φ=Re[χ]L。

(7)

基于T(x)的傅里叶变换和夫琅禾费衍射理论，得到夫琅禾费衍射方程

(8)

其中

(9)

代表一维空间周期夫琅禾费衍射。M是被探测光场照射的光栅沿着x轴的空间周期数。θ是相对于x轴的衍射角。λp是探测光场波长。归一化探测衍射强度，即令T(x)=1，则Ip(θ)=1。n阶衍射强度由方程(8)表示，其中x方向上sin(θ)=nλp/Λ。

2 分析与讨论

驻波场与原子相互作用使得依赖于泵浦场强的探测场吸收性质呈现周期性变化。通常来讲，在波腹处电磁诱导透明的出现使得探测场近乎透明传输；而在波节处无透明窗口，探测场被吸收。这样的介质好比经典物理框架内的周期刻蚀玻璃光栅。当探测场垂直于驻波场在介质内传输时，将会发生衍射。接下来我们将演示边频对电磁诱导相位光栅的影响并且分析该系统内各参数对于衍射效率的控制。

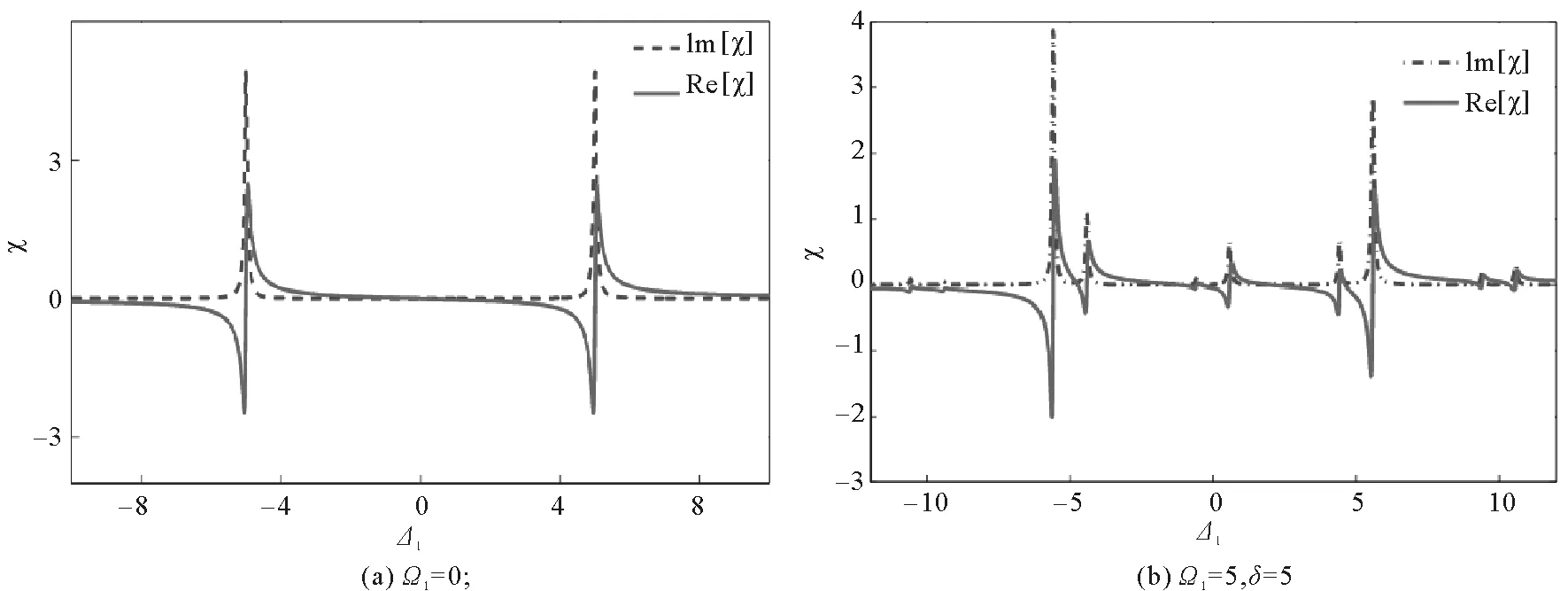
图2 吸收色散谱Fig.2 The absorption and dispersion spectra

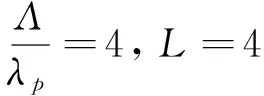
保持δ=5，继续增大边频强度，探测共振时的衍射强度对比如图4所示，其中实线对应Ω0=10、Ω1=10、Ωp=0.01，虚线对应Ω0=10、Ω1=5、Ωp=0.01。由图4可以看出，随着边频强度增大，边频相干引起的相位调控增强，一阶衍射强度在原来的基础上更加明显。为解释该条件下的增强效应，做出该条件(Ω0=10、Ω1=10、Ωp=0.01)下的吸收色散图如图5所示。图中显示，随着边频强度的增大，电磁感应窗口再次增多，吸收峰不对称加剧，探测共振频率处，吸收几乎为0，而色散增加，导致相位调制效应增强。

图3 归一化衍射强度Ip(θ)与sinθ之间的函数图Fig.3 The corresponding normalized diffraction intensity Ip(θ) as a function of sinθ

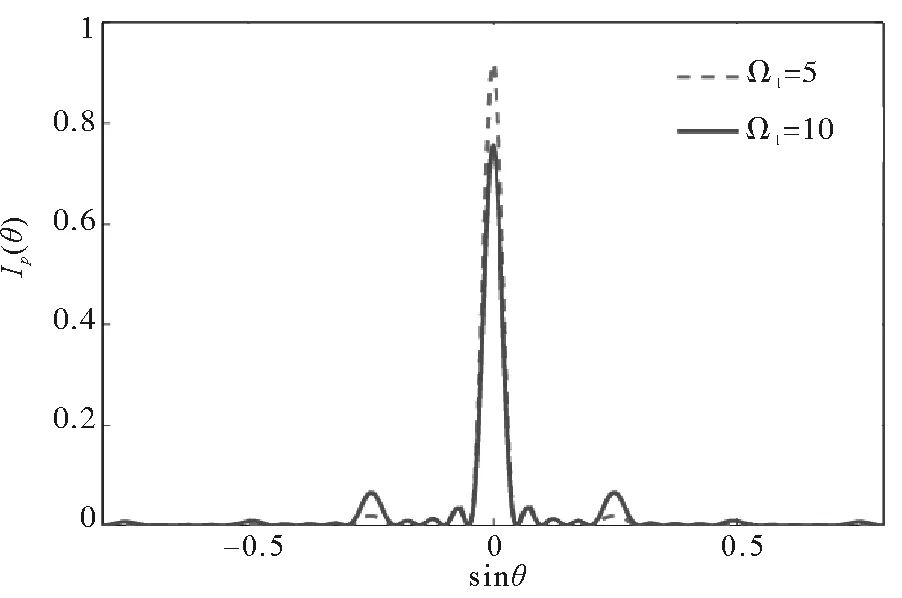
图4 衍射强度Ip(θ)与sinθ之间的关系Fig.4 The corresponding diffraction intensity Ip(θ) as a function of sinθ

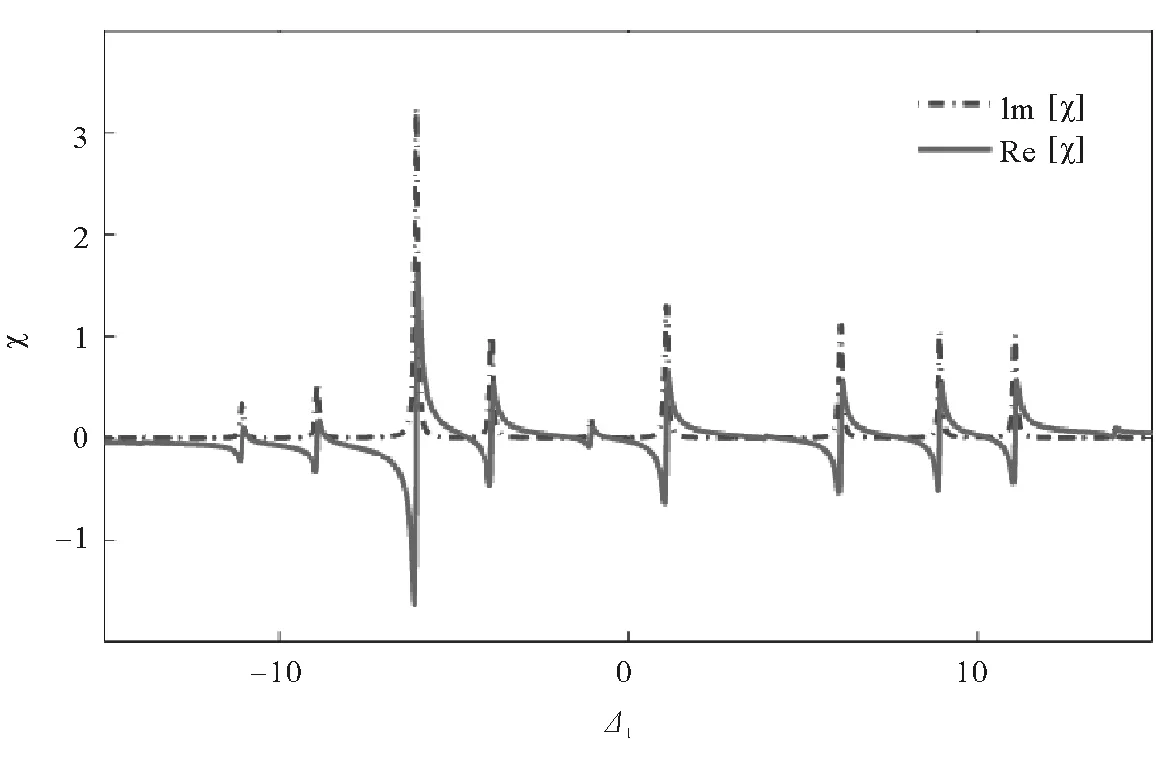
图5 吸收色散谱(Ω1=10)Fig.5 The absorption and dispersion spectra with Ω1=10

已知强度调节一阶衍射有限。从公式(6)、(7)可以看出，无吸收的非0色散可以更进一步增强电磁感应光栅的一阶衍射强度。保持泵浦场中心频率共振Δ2=0，利用图2(b)所显示的吸收色散性质，选择失谐为Δ1=-6.0，此时伴随吸收几乎为0出现较大的色散。基于边频相干(Ω0=10、Ω1=5、Ωp=0.01)，Δ1=-6.0(实线)时的衍射强度如图6所示，与中心频率处Δ1=0(虚线)的衍射强度图进行对比。随着Δ1的转移，探测场色散增强，并在Δ1=-6.0处达到较理想效果，使探测场透射良好，从而高阶衍射强度进一步增强。

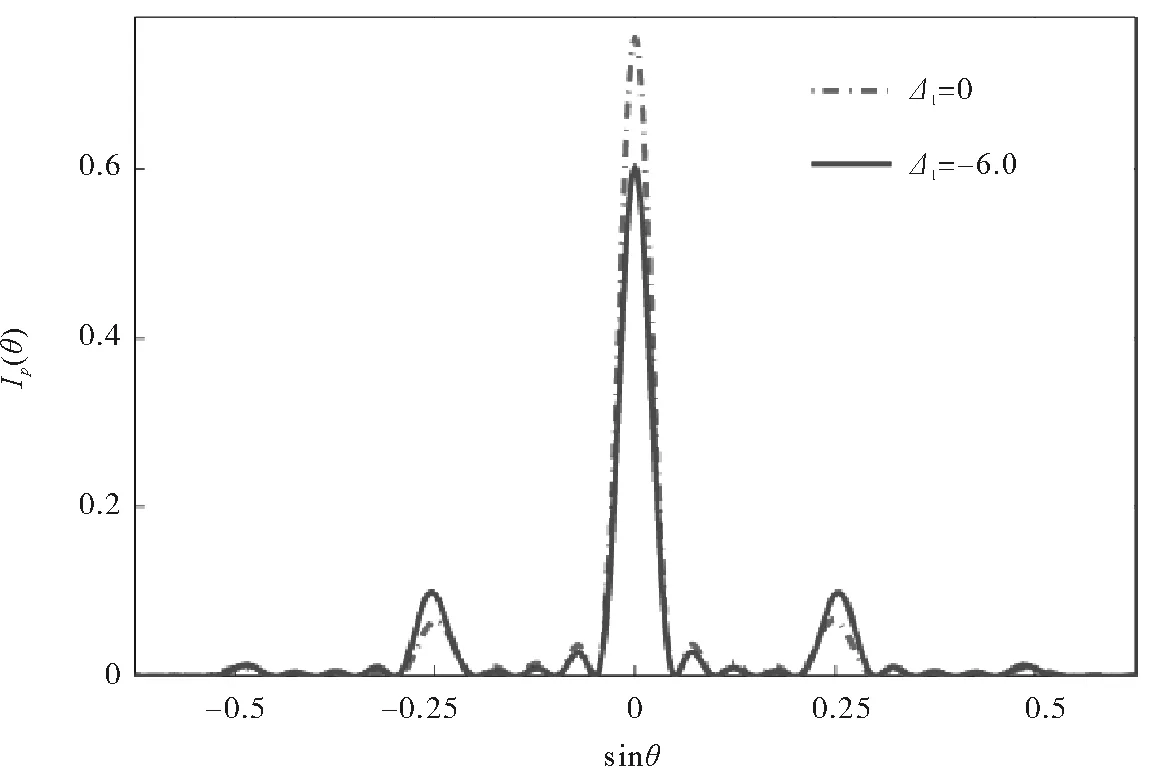
图6 衍射强度Ip(θ)与sinθ之间的关系Fig.6 The corresponding diffraction intensity Ip(θ) as a function of sinθ

本文也研究了边频强度Ω1的变化、光场与介质作用长度L的变化、以及泵浦场中边频与中心频率场间的频差δ的变化对衍射效应的影响。保持Ω0=10、Ωp=0.01和Δ1=-6.0、δ=5不变，得出一阶衍射强度与Ω1的关系如图7显示，随着Ω1的增强，一阶衍射效率先增长后衰减。在Ω1=6.3的位置，一阶衍射强度达到极值。调谐Ω1=6.3，保持Ω0=10、Ωp=0.01和Δ1=-6.0、Δ2=0、δ=5，得到图8所示一阶衍射强度与作用长度L之间的函数图。由图8可见，该条件下作用长度在L=6.5位置，一阶衍射强度达到极值。调控作用长度至L=6.5，保持Ω1=6.3，其他参数不变，在图9中做出一阶衍射强度与频差δ之间的关系。可见δ=5处一阶衍射强度最大。其他参数条件下，亦显示δ=5处衍射效应理想。总而言之，该系统中边频存在时，调谐合适的边频强度，选择合适的探测失谐、作用长度及泵浦场边频与中心驻波场频差及其他相关参数，利用边频相干效应可以增强相位电磁感应光栅中的一阶衍射强度，该调控下的衍射效应与单色场作用条件下相比较得到显著增强。一阶衍射强度对边频的依赖性可以用修饰原子态来解释[28]。

图7 一阶衍射强度Ip(θ1)与Ω1之间的关系(Ω0=10，Ω1=5，Δ1=-6.0)

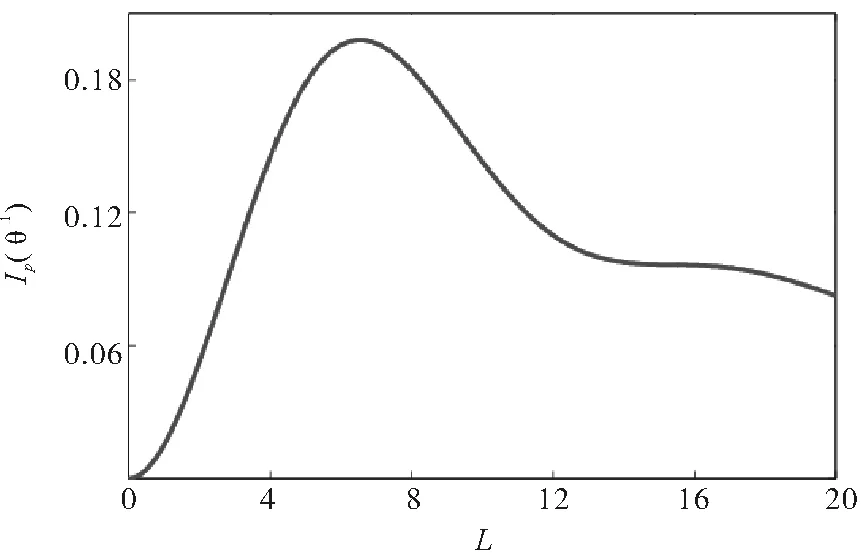
图8 一阶衍射强度Ip(θ1)与相互作用长度L之间的关系(Ω0=10，Ω1=6.3，Δ1=-6.0)Fig.8 The first-order diffraction intensity Ip(θ1) as a function of interaction lengthL withΩ0=10,Ω1=6.3,Δ1=-6.0

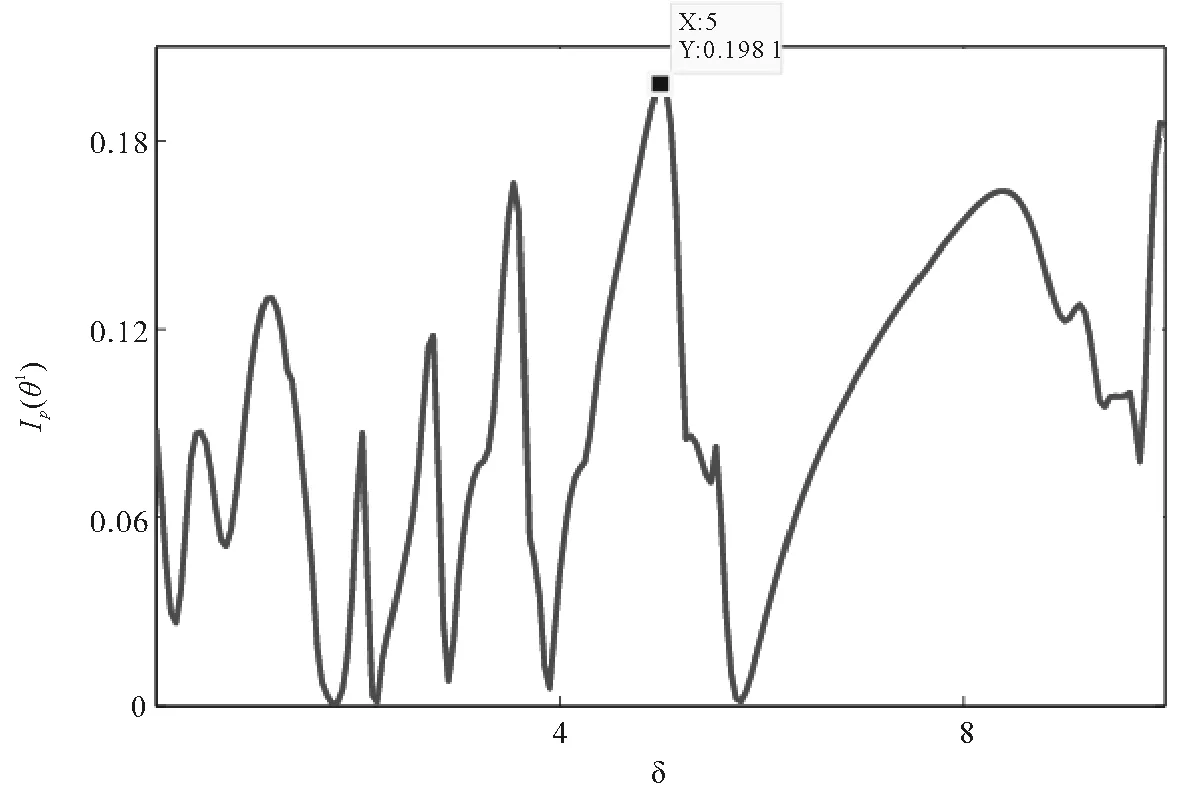
图9 一阶衍射强度Ip(θ1)与δ之间的关系(Ω0=10，Ω1=6.3，Δ1=-6.0，L=6.5)

3 结论

研究了三能级Λ型原子系统中边频相干对电磁感应相位光栅的影响，探讨了边频相干对光栅的形成及对衍射强度的影响。结果显示，该系统中电磁感应光栅效率对探测失谐及泵浦场中的边频强度极其敏感。调谐合适的探测失谐，调控边频强度及系统其他参数，一阶衍射效率显著增强，其值超过单色场控制下[4]的值近一倍。