开放课堂，让学生的思维悄然生长——“轴对称图形的认识”教学实录与思考

◇宋泉妹

一 游戏导入，激发兴趣

师：孩子们，你们看这是谁呀？今天的黑猫警长怎么有点与众不同呀？（出示只有一只眼睛的黑猫警长）那咱们赶紧来给它贴上另一只眼睛吧，不过你得蒙上眼睛来贴。

（学生蒙眼贴画）

师：大家评价一下，这位同学把黑猫警长的眼睛贴到最合适的位置上了吗？

生：蒙着眼睛，找不到位置，睁着眼睛贴就准了。

师：睁着眼贴就能保证贴在最佳位置上吗？

生：可以用尺子上下左右量一量，然后贴上去。

生：直接把图对折，然后照着另一只眼睛对称的位置贴上去。

师：对折后对准另一只眼睛贴确实是个好办法。

教学思考：为了把黑猫警长的眼睛贴到最准确的位置，去寻求最佳的解决办法，学生自然而然地想到最方便而又最准确的方法——对折，初步感知轴对称。在充满欢乐气氛的游戏情境中，学生不知不觉进入“课堂角色”，将一个数学概念转化成了具有探究性的数学问题，开放了学生的思考空间，把生活经验与数学学习紧密联系起来，大大激发了学习的热情。

二 探索特征，辨析理解

1.学习例题，初步感知。

（1）师：（课件出示由蝴蝶、天坛、飞机的实物图转化成的平面图形,如图1）从数学的角度来观察这些图片，它们有什么共同的特征？

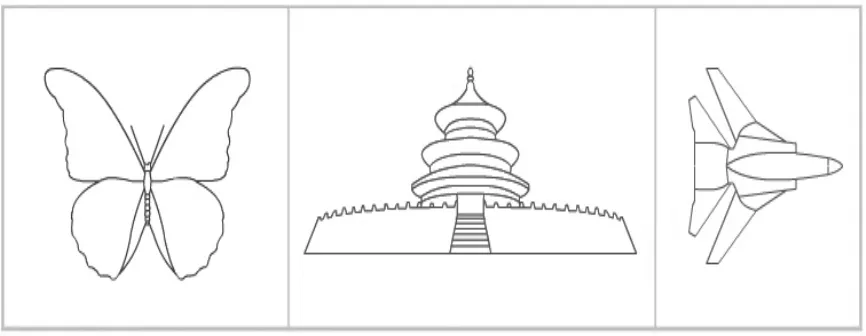
图1

生：图形的两边，大小和形状都一样。

生：图形的两边都是一模一样的。

生：图形的两边完全一样，是对称的。

师：大家通过观察，都认为两边是完全一样的，但数学是讲道理的，谁能想个办法来验证我们的发现？

生：可以把这几个图形对折，看看能否重合。

师：你真是一个会思考的孩子，大家按照他的方法动手验证吧。

（课件出示活动要求：①拿出1号信封中蝴蝶、天坛、飞机的图片。②把每个图形都对折。③和同桌说说你的发现）

（2）汇报研究成果。

师：通过验证，你得到了怎样的结论呢？

生：我发现蝴蝶图片对折后，两边都是角对角、边对边，一模一样。

生：我发现把天坛和飞机的图片对折后，两边是完全重合的。

师：我们把具有这样特征的图形叫作轴对称图形。谁来说说什么是轴对称图形？

生：图形两边完全一样的图形就是轴对称图形。

生：把图形对折后能完全重合的图形。

师：这是大家对轴对称图形的初步认识，要想深究还得继续学习。

2.深入探究、辨析理解。

师：你知道这是什么字吗？

生：像一个人。

生：两个“人”是“从”。

师：如果把这甲骨文的“从”字看成一个图形，它是轴对称图形吗？

生1：“从”字是轴对称图形，它的两边完全相同。

生2：我不同意他的想法，判断一个图形是不是轴对称图形，要把图形对折后，看它能否完全重合。“从”字的一边翻转过来，就不能完全重合了，所以不是。（学生操作演示）

师：通过对这个图形的判断，说说你对轴对称图形新的认识。

生：两边完全一样，对折后不一定能完全重合，完全一样和完全重合是两个不同的概念。

生：对折后能完全重合的图形，叫作轴对称图形。

生：把图片竖着对折，两边完全重合，是轴对称图形。

教学思考：学生通过观察实物图片，初步体会到生活中的对称现象。把实物图片抽象成平面图形加以操作，让学生经历由具体到抽象的过程，再通过同桌间的探讨对轴对称图形的基本特征有了一个初步的认识。此刻他们对“轴对称图形”的概念还是比较模糊的，只是停留在看上去两边大小、形状一样的层面，不会自觉地把图形“对折”后再看看是否“完全重合”，以为“完全一样”和“完全重合”意思是一样的。在此基础上，创设了甲骨文中的“从”字这一反例，让学生发现看上去两边完全一样的图形对折后不一定能完全重合。

三 层层递进，丰盈理解

师：轴对称图形肯定不止这几个图形，让我们继续寻找吧。回想一下，我们学过的最简单的平面图形有：长方形、三角形、平行四边形、正方形、圆……想一想，它们都是轴对称图形吗？（自由回答，不予判断）口说无凭，动手操作或许会带给我们更多有价值的结论。

活动要求：①拿出2号信封中的图形（长方形、正方形、等腰三角形、非等腰三角形、一般平行四边形、圆）。②自己想办法验证哪些图形是轴对称图形。③与小组里的同学说一说你的发现。

1.长方形。

学生一致认为长方形是轴对称图形。

师：老师把长方形对折，（如图2）发现两边没有完全重合，它还是轴对称图形吗？

图2

生：把长方形横着折或竖着折，都可以使两边完全重合，所以长方形是轴对称图形。

生：判断一个图形是否为轴对称图形，只要能找到一种折法让它的两边完全重合，就可看作轴对称图形。

师：总结得真到位。如果把这个长方形变大、变小，改变方向，它还是轴对称图形吗？

生：还是轴对称图形。

师：这说明了什么？

生：说明长方形无论变大、变小还是改变方向，只要它的形状没有发生变化，还是长方形，那它就是轴对称图形。

2.三角形。

师：出现了两种意见，怎么证明你的观点？

生：我把这个三角形（等腰三角形）对折，发现两边完全重合，所以我认为三角形是轴对称图形。

生：这个三角形（非等腰三角形）无论怎么对折，我发现都不能使两边完全重合，所以我认为三角形不是轴对称图形。

师：这又说明了什么？

生：说明了三角形是个大家族，有的是轴对称图形，有的不是轴对称图形。

3.平行四边形。

学生都认为平行四边形不是轴对称图形。

师：你怎么证明？

学生边演示边说：平行四边形无论怎么对折都不能使两边完全重合。

师小结：平行四边形虽然折痕两边的部分完全一样，但都不能使两边完全重合，所以不是轴对称图形。

4.正方形。

师：说说你是怎么折的。

生：横着、竖着、斜着对折都可以使两边完全重合。

师：正方形变成正八边形还是轴对称图形吗？

生：正八边形还是轴对称图形。

师：圆呢？有多少种折法？

生：圆有无数种对折的方法都可以使两边完全重合。

师：如果在圆中加入图案后它还是轴对称图形吗？（如图 3）

图3

师：请你选择一个自己熟悉的图形再来说说你的判断。

生：工商银行的标志是轴对称图形，它可以横着对折也可以竖着对折。

生：澳门的区徽是轴对称图形，可以竖着对折。

生：香港区徽不是轴对称图形。

教学思考：对这些简单平面图形的判断看似是重复的操作，实质是学生对轴对称图形的概念理解不断深化的过程，在反复的点化、持续的浸润下，不断纠正、完善对轴对称图形的认识，学生的判断力逐步得以提升。把正方形演变成正八边形再到圆，有多种对折的方法，但在图形中加入图案后，再进行辨别，明确了部分重合与完全重合的区别。这样的设计既有利于学生从不同角度体会轴对称图形的特征，也有利于让学生的思维在广阔的时空领域中自由翱翔后再逐步走向深入。

四 趣味练习，延伸探究（略）