“邮票的张数”两种不同时期教材的比较

◇原素芳

“邮票的张数”是列方程解决问题的学习内容，本文试图结合根据实验版课标编写的北师大版实验教材（以下简称实验版），以及根据2011年版课标修订后的北师大版教材（以下简称修订版），对此部分内容进行分析和比较。

一、教材结构的对比分析

此内容在两种不同版本教材中的内容安排，如表1所示。

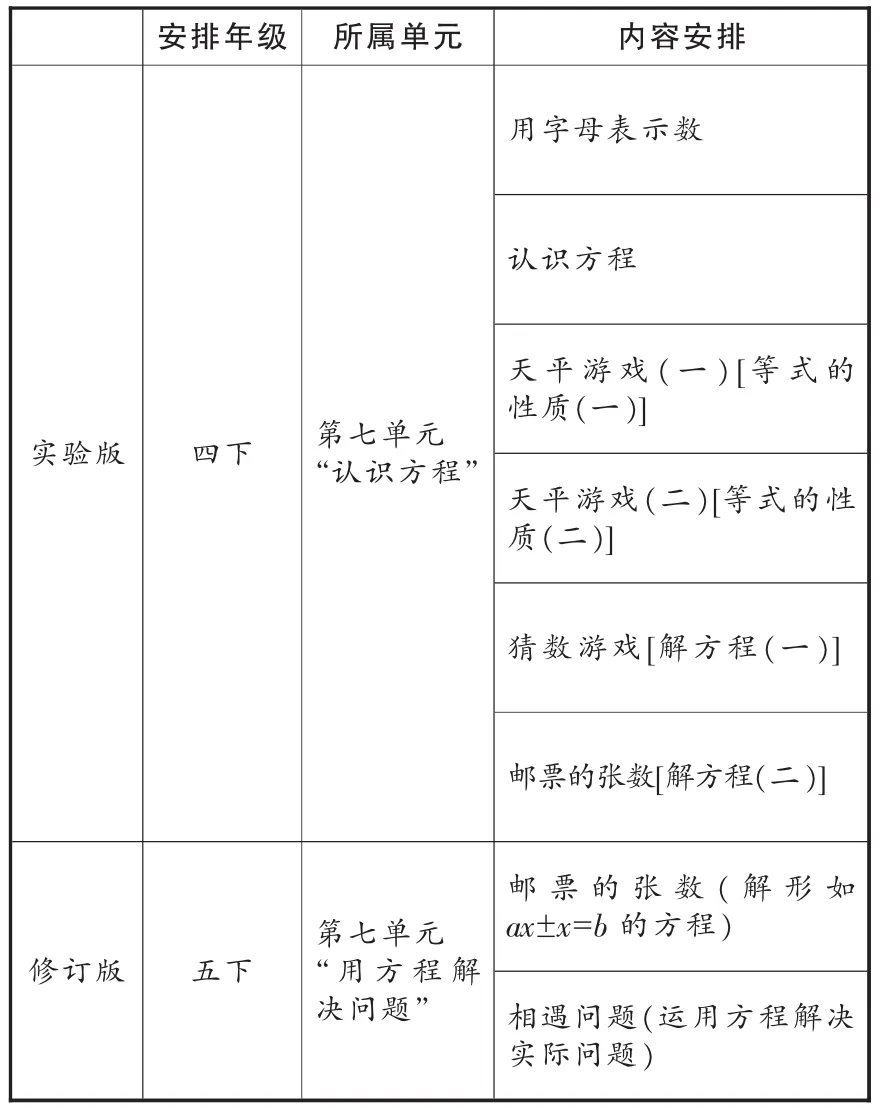
表1

观察表1，可以看出，相对于实验版教材“邮票的张数”这个内容，在修订版教材中呈现了这样的变化：教学内容后移，隶属单元不同。这两处变化体现了编者对知识之间联系的不同理解。“邮票的张数”“相遇问题”这两节课在修订版中的编排顺序都做了调整，修订版教材把原先“认识方程”单元最后一课“邮票的张数”，与“数学与交通”第一课“相遇问题”组建为“用方程解决问题”单元，这样将方程模型的运用作为一个独立的单元，有助于学生积累把实际问题中的数量关系抽象为方程的经验，体验方程是刻画现实世界的模型。

另外，从分散教学难点这个角度看，学生在四年级初步认识方程，五年级再来研究用方程解决问题，拉长了方程知识的学习时间，也体现了对“列方程解决问题”的整合，有助于学生更好地体验、感悟方程思想。

二、教材内容的对比分析

1.素材的“多”与“简”。

从情境图的呈现来看（如图1），实验版中是4人3句对话，修订版教材则是3人2句对话。相比较而言，修订版教材少了1个人物（爸爸）、1句对话和1个问题，还少了妈妈看报纸的动作、地板图、绿色植物。删除这些对话、动作和图案，排除了这些非主题因素对学习主体的干扰，一方面让情境图呈现更简洁、主题更突出，另一方面有利于学生更好地读取数学信息。

图1

2.问题的提出。

实验版教材直接在情境图中呈现问题（如图1），并且是和主情境图放置在一起的；修订版教材在出示情境图后，留给学生思考的机会和时间，鼓励学生通过读取信息自主尝试提出数学问题（如图2）。修订版教材注重让学生“初步学会从数学的角度发现问题和提出问题”，这与2011年版课标提出的“增强学生发现和提出问题的能力”的总目标是吻合的。

图2

3.直观图的表示。

实验版教材呈现了一幅线段图和一个等量关系式（如图3），它选取两个信息，即“姐姐邮票的张数是弟弟的3倍”和“我和姐姐一共有180张邮票”来引导学生画线段图分析数量关系，找出“姐姐的张数+弟弟的张数=180”这一等量关系。

图3

修订版教材是以两幅学生作品的形式（如图4），启发学生从多角度分析数量中的相等关系。

图4

其中一幅作品是文字描述，出现两个等量关系式：“姐姐的邮票张数+弟弟的邮票张数=180”“姐姐的邮票张数=弟弟的邮票张数×3”。这两个关系式是从两人的对话中提炼出来的。两人的对话是生活语言，而提炼出来的关系式是抽象加工后的等量关系式，是数学语言，也是方程的雏形。

另一幅作品是方格图，将刚才得出的两个等量关系式转化成方格图，这样的图形语言让数量关系显得简洁、清楚。

最后，教材出示学生的话语：“我知道了，如果设弟弟的邮票为x张，姐姐就有3x张……”表面上看这是回答前面的问题，实际上是学生对图形语言的理解，揭示了设置未知数的方法，即把1倍数——弟弟的邮票张数用未知数x表示，那么3倍数——姐姐的邮票张数就可以用3x表示。这样便把两个未知数转化为了一个，降低了后面列方程和解方程的难度，为体会列方程解决问题的优越性埋下伏笔。

4.列方程解决问题。

两个时期的教材都给出了完整的列方程、解方程的过程（图略）。这是帮助学生明白列方程解决问题规范的书写格式，体会方程解法。两种教材都给出了这样的话：“1个x与3个x合起来是4个x。”旨在从加法意义的角度让学生理解4个x的意义，这样将较复杂的方程转化为简单的方程，将新问题转换为旧知识。稍有不同的是，修订版教材在解方程后采用留白的方式让学生自己写答语，加强学生的反思意识，让学生经历列方程解决问题的全过程，这与之前的编排是一脉相承的。

5.题目信息的变换（如图5）。

图5

关于题目信息的变换，两个时期的教材表述略有不同，实验版教材是要求利用“姐姐比弟弟多90张”这条信息仿照例题进行解答，修订版教材是变换题目中的信息之一，提出新的问题，让学生再次经历方程模型的建模过程，增强学生提出和发现问题、分析和解决问题的能力。

6.练习的设置（图略）。

教材对应的后续练习，实验版教材安排了2次。先在例题后安排了“试一试”，然后安排“练一练”，一共4道题。“试一试”和“练一练”第1题巩固解形如ax±x=b的方程的方法；第2题是列方程解决问题（情境对话式），与例题学习结构类似；第3题是新的情境，等量关系相对简单，只出现了一个未知量。修订版教材安排了6道题。第1题是配合问题串，鼓励学生再次经历解决问题的过程：先读懂题意，根据信息找出等量关系，再根据等量关系列出方程求解。不同的是，选择了新的情境，从而帮助学生再次体会方程的含义。第2题侧重运用解方程的方法直接解ax±bx=c这样的方程。第3～6题则是鼓励学生在新的情境中，综合自己对于题意、等量关系等的理解来解决问题。

三、教学启示

通过上述方面的比较，对比两个时期教材的变与不变之处，会给我们的教学带来哪些启示呢？

1.用方程解决实际问题，要重视在现实背景下分析题目中的数量关系。寻找数量间的相等关系是列方程解决问题的首个关键步骤，它对下一步列方程解题起到了铺垫作用。如修订版教材的练一练第1题明确提出先找等量关系，第3～6题让学生多次经历寻找数量关系、列方程求解的全过程。

2.立足用方程解决问题意识的培养，形成恰当的解题策略。方程意识是学生在解决问题时，一种能主动判断并选择是否用方程解决的意识。由于学生在低年级开始就用算术思路解决问题，解题时习惯了从已知到未知，而到了四、五年级，受思维定式的影响，不少学生不习惯列方程解决问题，因此，教学时要注意引导学生对比方程方法与算术方法，感受用方程解决问题的优越性。久而久之，学生在面对新的问题情境时，就会主动判断是否用方程方法解决问题，并通过比较和分析，正确选择恰当的解题策略。

3.列方程解决实际问题不仅仅是为了解题，更重要的是数学建模思想的渗透。修订版教材比实验版教材更注重让学生经历方程模型的建立过程，渗透方程思想。修订版教材的编排，表面上看是“情境+4个问题”，实际上是按“创设情境—抽象数量关系—建立方程模型—解决问题”这样的顺序编排的，目的就是让学生经历完整的用方程解决问题的全过程，建立方程模型，进而体会方程思想。