“三角形边的关系”教学设计与思考

◇脱中菲

一、内容分析

三角形边的关系是学生在初步了解三角形定义和分类的基础上，从“边”的角度研究三角形的特征，即研究三角形边的关系存在“三角形的任意两边之和大于第三边”这一事实性特征。这一知识的本质是由欧式几何中“两点之间直线段最短”这一公理在三角形内容上的推论。这一公理，学生在三年级时已经学习过。这一特征可以用来作为判断“三条线段能否围成三角形”的依据，即学生只需要用两条较短边之和与第三条边进行比较，就可以判断出来，这是判定性的知识。所以，学生在本节课不仅仅要学习事实性的知识，还要初步理解事实性知识与判定性知识二者之间的关系。

北师大版教材在编写上充分体现了探究与发现的学习方式，共设计了三个问题：首先，学生进行自主用小棒围三角形的活动，思考“能否围成三角形与什么有关”，体会影响能否围成三角形的因素是边的长度。其次，引导学生研究 “什么样的三根小棒能够围成三角形”，学生初步发现只要两条较短的边之和大于第三条边，就能够围成三角形。这也是学生对判断能否围成三角形的“依据”的学习。再次，针对能围成的三角形来研究三边存在什么样的关系。教材中的设计侧重于探索与发现，通过设计操作活动，让学生在观察、操作、比较的过程中推导出三角形三边关系的特征。

二、教学过程

活动一：提出问题，大胆猜测。

教师为学生提供一种扣条，进行围三角形的游戏。

师：同学们，今天我们用扣条代替小棒玩围三角形的游戏，好吗？老师为大家准备了五组不同的扣条，请同学们任意选一组扣条，把扣条当作小棒用，看看谁围得又快又好！

设计意图：教师准备的5组不同的小棒中，有的可以围成，有的无法围成，通过这个游戏让学生了解到不是任意的三根小棒都能围成三角形，引发思考。

师：我看到好多同学都围成了，你们的手真巧！（故意疑惑）怎么了？有同学遇到困难了。还有好几位同学说围不成三角形，是吗？谁的那组小棒摆不成？

（教师让学生分别将围成的和围不成的小棒放到投影仪上展示）

师：同学们，看到这个情况，你有什么想说的吗？

生：有的三根小棒能够围成三角形，有的不能围成。

师：看来不是随便拿出三根小棒都能围成三角形。那么，你们觉得能否围成一个三角形与什么有关系呢？

生：与边有关。

生：如果两条较短的边都再长一些就能围成三角形了。

师：好，那我们今天就来研究一下，怎样的三条线段能够围成一个三角形。

设计意图：在北师大版和人教版的教材中，该内容都是以四组长度不同的边作为学习内容的起点。这样设计的思路是用已知的长度去围三角形，按照这样的实际，学生首先关注的应该是“边”。但是正如我们对学生经验的分析，学生对三角形的整体认知，不能一下子聚焦到边的长度这一问题上，因此按照教材中直接给出不同的边的长度，对学生来说有些突然，而从三角形入手，以游戏的方式围三角形，学生通过观察和对比已经围成的三角形和没有围成的图形，能够初步意识到：能否围成三角形与边的长度有关，与三角形两条较短的边有关。这样的设计，一方面让学习在学生已有的经验基础上展开，另一方面，也让接下来的探究活动更具有目的性和方向性。

活动二：小组探究，发现规律。

教师出示小组学习任务：怎样的三根小棒能摆成三角形？并提出学习要求：①将小组中围成三角形的小棒放一组，围不成三角形的放另外一组。②对比这两组小棒，按顺序和同学说一说你的发现。

教师提示：组员分别观察围成的三角形，看看三角形的边有什么样的特征；再仔细观察没有围成三角形的小棒，看看它们的长度有怎样的特点。

5分钟后，教师组织学生依次汇报。（见表1）

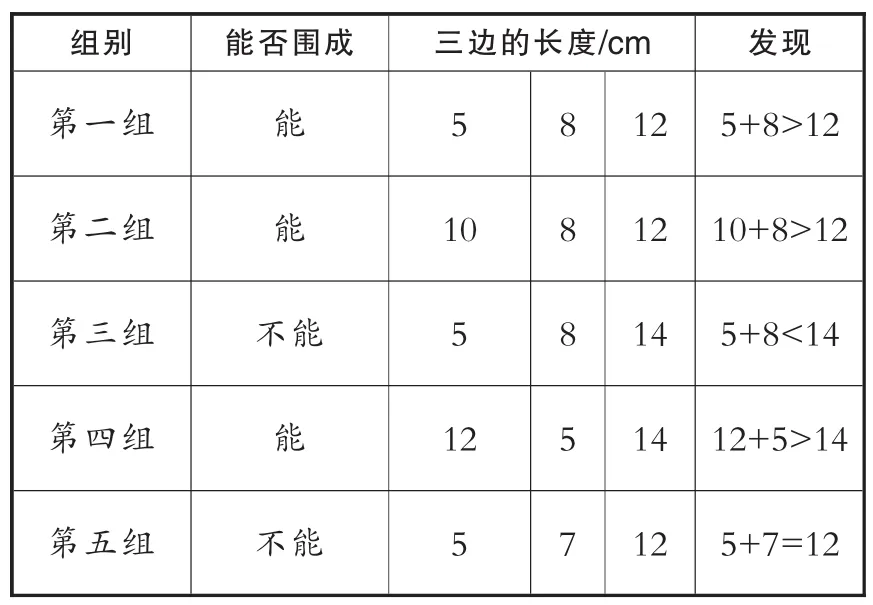
表1

学生首先汇报了各组所用的三根小棒围三角形的情况（能或不能），接着汇报了三条边的长度。

师：同学们仔细观察黑板上的这些数据，我们将能围成三角形的分成一类，将不能围成三角形的分成一类，然后仔细观察一下，这两类不同情况的小棒长度有什么规律吗？

学生在教师的引导下，逐渐归纳出：在这五种情况中，能围成三角形的三根小棒中，较短的两条边之和大于第三条边。不能围成三角形的三根小棒中，较短的两条边之和小于或者等于第三条边。

设计意图：①探究活动不止步于观察和操作，而是在数学经验的积累过程中发展抽象思维。本环节从观察实物到借助数据进行验证进而发现规律，其目的是让学生逐步抽象发展空间观念。②小棒的数据并非教材中事先设计好的，而是学生基于学习需要主动获取的，体现了学习的生成性。③基于两种情况进行分类比较，经历从个别到一般的过程，是不完全归纳的数学思想在教学中的渗透。学生在此处，结合之前游戏中的猜想和图表中的数据，结论的得出便水到渠成了。

师：同学们，从刚才拼摆的五组小棒中，我们发现了三角形边的奥秘。那么老师这里还有这么多三角形（大屏幕出示不同的三角形，图略），你说它们的边都具有刚才你们得出的那个结论吗？

生：我觉得应该具备，我们可以量量它们的边的长度。

师：这么多三角形我们能挨个量吗？

生：不用，我认为三角形一定满足两条较短的边大于第三条边的条件，因为三角形要拱起来（做手势），否则就拱不起来。

师：看来给出三根小棒的长度，我就只需要判断两根较短的和与第三根小棒之间的关系就能够判断能否围成三角形了，对吗？

学生点头表示同意。

活动三：反向猜测，推理论证。

师：既然我们通过计算就能够判断出三根小棒能否围成一个三角形，那么，思考一下：三角形的三条边有什么特征呢？谁能说一说？

生1：两条较短的边之和大于第三条边。

师：好，这个观点同意吗？他关注到了较短的两条边和第三条边的关系，还有其他观点吗？

生2：最短的边和最长的边的和也大于第三条边。

师：为什么呢？你的根据呢？

生2：两条较短的边的和都比第三条大了，那么最短的边和最长的边的和也大于第三条边。

师：他的观点大家听清了吗？什么意思呢？

生3：就是随便两条边的和都比第三条大。

师：“随便”，这个词挺好，还能换个词吗？

生4：任何两条边，任意两条边。

师：刚才同学们猜测是三角形的三条边中任意两条边之和都大于第三条边，你们同意吗？

有的学生点头，有的摇头。

师：那我们来验证一下，请各小组验证刚才我们已经围成的三角形的三条边的关系。

师板书：三角形任意两边之和大于第三边。

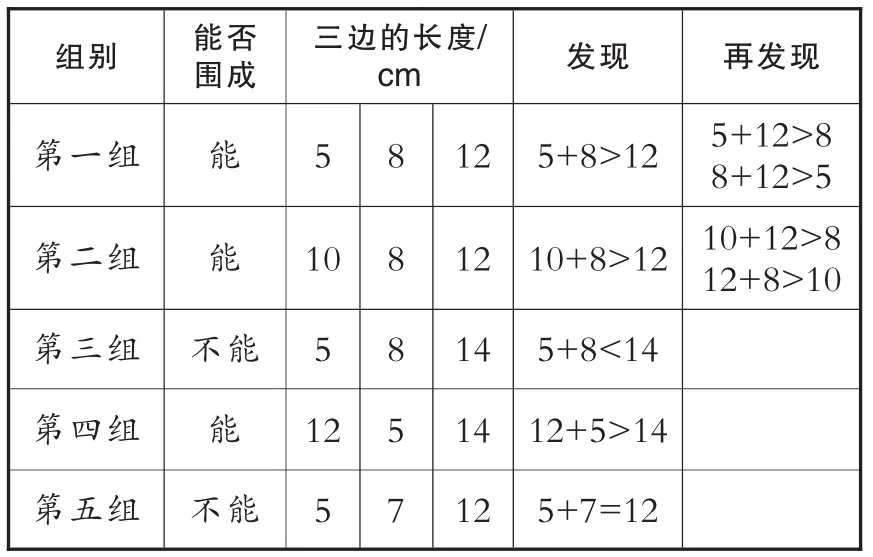
表2

汇报两组后，有一个学生发言。

生：老师，我们不用再挨个算了，第三组也是这样的规律。

师：为什么不算了？

生：较短的两条边的和都比第三条大，那么任意的两条边的和一定比第三条边大。

师：你们同意吗？真的不用再算了？那关于三角形的三条边你们发现什么特征了？

生：任意的两条边的和都大于第三条边。

设计意图：从二次猜测到尝试验证，再到演绎推理，学生直接从数据中推导出三角形三边的特征，经历了从归纳到演绎的过程，学生的抽象思维得到进一步发展。

活动四：揭示本质，关联生活。

师：（出示图1）小明想从点A到点C，你建议他怎么走？说说为什么。

图1

生：小明可以从A到B再到C，也可以直接走到C。

生：要想尽快走到C，我认为应该直接从A走到C。

师：为什么呢？

生：因为我们可以把ABC看成一个三角形，三角形的两条边之和一定大于第三条边。

生：我们以前学过两点之间直线段最短，AC就是最短的直线段，其他路都得拐弯。

师小结：你们都同意吗？其实我们今天学习的三角形三边关系和以前我们学习的“两点之间直线段最短”的线段公理是密切相关的。我们今天不仅学习了新知识，还找到了新知识和以前学习的知识之间的关系，你们太棒了。

师：同学们，其实生活中有利用三角形边的关系改进交通的案例，比如杭州市专门设计了这样的路口（出示图2）。看来我们今天学习的数学还真能解决生活中的大问题。

图2

设计意图：选择路线的问题考查的是学生从多个角度思考解决方案的道理和依据，进而引发学生主动将三角形三边关系本质归结到线段公理这一知识本源。这一环节教师点到为止，让学生在讨论与分析过程中，主动打通知识之间的联系，在恍然大悟之后深化认识。