论证视角下的“三角形内角和”教材理解与教学设计(五)
——该用哪些例子来说明三角形内角和是180°
◇宋煜阳

什么是运用论据进行说理的思维习惯?主要表现为学生不仅知道这个结果,而且能通过推理或举出事例让自己或他人确信这个结论是正确的。具体到“三角形内角和是180°”这个结论,就要从“我知道三角形内角和是180°”转向“我该用哪些例子来说明三角形内角和为什么是180°”的例证思考。当然,能够运用例证思考的基础是学生首先得有说明三角形内角和是180°的数学实例,然后选取适切的例子加以论证。那么,各版本教材在前期编排中提供了哪些论据支持呢?又该如何认识这些经验性论据?笔者仅从经验性论据支持的视角对人教版、苏教版、北师大版、浙教版、台湾教材等进行比较分析。
经验性论据一:直角三角形所构造的例证事实
在角的度量单元,大陆教材都设计了测量三角尺的内角和与利用三角尺拼组画角的活动,帮助学生明确了这两个直角三角形每个角的具体度数,并在三角尺拼组画角活动中熟记了“30°,60°,90°”和“45°,45°,90°”这两组常用数据。出于对数据的敏感,学生已经能感知这两个直角三角形的内角和是180°。而像苏教版教材,索性给出“每块三角尺上三个角的度数和各是多少度”的问题讨论(如图1),明示了这两个直角三角形内角和是180°这一数学事实。

图1
教学实践表明,在三角形内角和的例证中,多数学生能够把这两个直角三角形内角和的结果作为论据进行提取,成为名副其实的经验性论据。问题在于,直角三角形有无数个,这两个直角三角形不仅在例证的数量上显得少,而且在例证的性质上属于特殊直角三角形,不具有一般性,甚至有可能使学生误解直角三角形只有这两种情形。作为三角形内角和的论据,直角三角形是三角形的特殊例证,而“30°,60°,90°”和“45°,45°,90°”两组数据的直角三角形是直角三角形的特殊例证,如何处理好例证的特殊与一般关系,是寻找经验性论据支持的重要视角。如在台湾教材中(如图2和图3),就非常强调从特殊直角三角形到其他直角三角形,从直角三角形到不是直角三角形的三角形的论证思路,处理非常细腻。台湾教材给我们的启发是,在前期角的度量活动中,适度扩充直角三角形个数与类型,有利于学生寻求到更多、更为一般的例证,在后续学习中运用论据进行说理的活动才能更为充分和深入。

图2

图3
经验性论据二:等边三角形所构造的例证事实
等边三角形(正三角形)每个内角是60°,也是证实“三角形内角和是180°”的特殊经验性论据。在“等边三角形每个内角相等”“等边三角形每个内角是60°”两个数学事实面前,各版本教材之间存在较大差异。台湾教材(如图4和图5)先通过对折方法得出等边三角形三个角大小相等,再通过测量得出每个角都是60°这个结论。而人教版是一次性得出“等边三角形三个角都相等”“等边三角形每个角都是60°”这样的结论(如图6)。
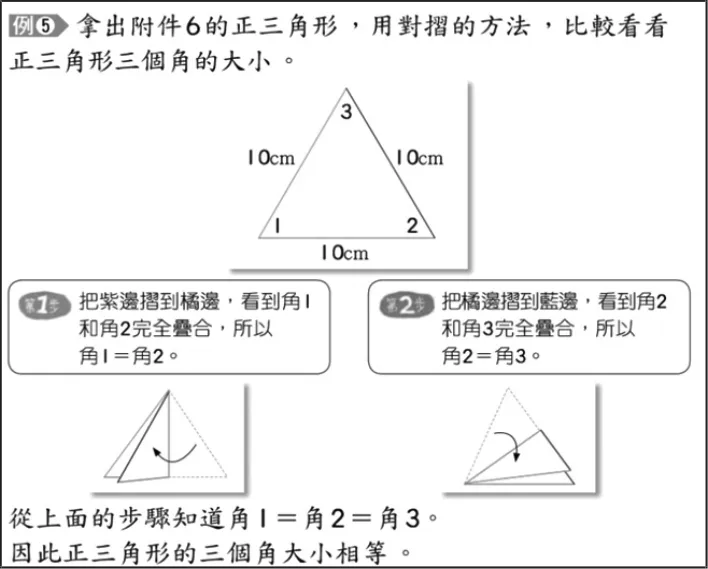
图4
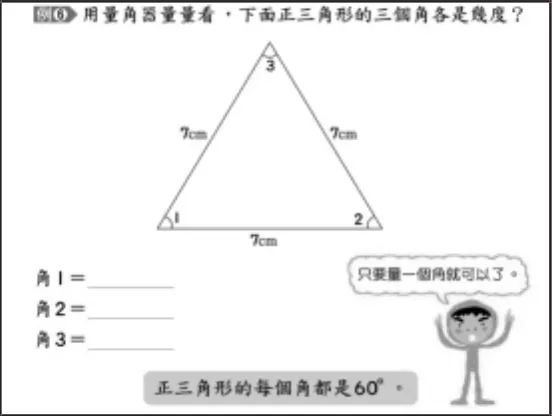
图5
这些版本教材在编排顺序上都把等边三角形相关内容安排在“三角形内角和”一课之前,都可以作为特殊的经验性论据使用。在实际教学中,相对于两个特殊直角三角形例证的调用,等边三角形例证被调用的几率很低。因此,从经验性论据积累角度而言,在前期“三角形分类”一课学习中,要加强学生对“等边三角形三个角都是60°”特点的刺激与识记;在后续“三角形内角和”一课的学习中,要适度引导学生关注这个特殊例证的调用。
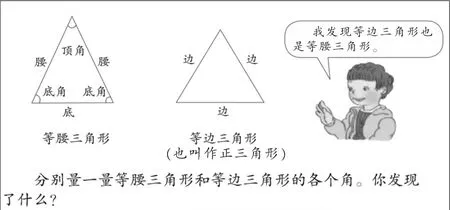
图6
经验性论据三:长方形与直角三角形之间形成的关系例证事实
在“三角形内角和是180°”例证中,个别学生能够把长方形分成两个直角三角形,根据“长方形四个角是直角、内角和是360°”这一数学事实,通过对角线分割推算得出每个直角三角形的内角和是180°。与这种“长方形一分为二”分割思路相近的是,台湾教材给出了“两个全等直角三角形合拼成长方形”的拼组思路。值得关注的是台湾教材在前期“直角”学习中明确指出“长方形和正方形的四个角都是直角”这个结论,并引入全等图形概念。
无独有偶,在三角形内角和一课的练习中,苏教版、北师大版、青岛版等教材都安排了长方形、正方形纸翻折或直角三角形合拼成长方形、正方形,观察讨论每种图形内角和,感受图形之间的关系。不同的是,苏教版、北师大版教材是把长方形、正方形内角和作为原有的数学事实使用,而青岛版教材是根据 “三角形内角和是180°”这个结论来推出长方形、正方形内角和。
如果说前文的经验性论据一和二是直接可证的话,这种利用长方形和直角三角形之间关系的论据则是间接的、需要转化的,推理要求更高一些。在强调推理思想的当前受到了较高的关注,不少教学设计就使用了这个论据。
考虑到论据提取的可行性和有效性,笔者对教材的前期编排提出三点建议:一是在“长方形、正方形的认识”一课进一步强调四个角是直角,甚至可以把内角和为360°列入特征范畴。二是理清长方形、正方形和直角三角形概念的上下位关系,为两种图形之间的分割、拼组提供逻辑依据。三是引入全等图形概念,便于形成较为严密的图形变换关系。
培养学生的推理能力,教学中必须增强运用论据进行说理的意识,相应地教材必须多视角、多渠道提供合理有效的例证事实,真正让学生有理可说、有例可证。

