猜测引发探究论证实现建构——以“小数乘小数”为例

◇陈 云

数学课堂应该给学生提供主动思考与建构数学知识的机会。教师在课堂上应创造机会，让学生进行主观猜测活动，激发学生的探究欲望。但是猜测不一定都是有效的、正确的，为了检验猜测是否合理、有效，数学论证也随之发生。可见，主观猜测活动不仅是启动学生主动思考的引擎，也能启动数学探究和引燃数学论证。

一、主观猜测引发探究欲望

主观猜测与数学猜想之间还有一段距离，学生更多的是凭借直观感受和学习中产生的数学灵感作出原始的判断。而这种凭借直觉作出判断引发后续研究的方式，更适合小学生的数学探索活动，它成为数学课堂上解决问题过程中的一个起始环节，整个猜测活动应包括四个历程：说出猜测、检验猜测、不信任猜测和获得感觉。

在教学北师大版教材四年级下册第三单元中的“小数乘小数”（街心广场）一课时，我创造了这样的机会：关于小数的运算我们学习了哪些？你可以猜想一下小数乘小数该怎样计算。学生的主观猜测活动就此展开，四个历程具体表现为六个阶段。

1.组织、观察题例。学生需要从已有的知识系统中列举相关题例，并组织起来。如学生会从已经学习的小数的有关运算中获取有限例子，并开始观察：1.23+3.8=5.03，4.75-1.8=2.95，0.2×2=0.4。

2.寻找规律。学生从组织好的资料中寻找规律，使所发现的规律也可以适用其他没有列举出来的例子。如小数加、减法是按照整数加、减法的计算方法进行计算的，小数点要对齐。小数乘整数也可以按照整数乘法的计算方法进行计算，积与乘数的小数点对齐。

3.形成猜测。学生整合自己的发现，形成了初步的认识，并且愿意将自己的猜测进行数学化的表达。如小数乘小数的计算方法是：按照整数乘法的计算方法进行计算，积的小数点要和乘数的小数点对齐。

4.寻找证据。“用证据支持假设”是学生数学探究能力的基本体现，学生期望从已有的知识系统中找出证明自己猜测的证据，这是对猜测的一种检验，也是尝试将猜测一般化的起始阶段。如：0.3×2=0.6，0.3×4=1.2。

5.列举反例。在教师的适度干预下，学生对刚刚的“妄下定论”谨慎起来，开始扩展更多不同类型的例子，检验猜测是否正确，并尝试找反例来推翻或完善原猜测，例如：0.3×0.2等于0.6吗？

6.产生探究欲望。学生感觉到了0.3×2与0.3×0.2的结果不可能是一样的，那么这个猜测就存在问题，小数乘小数的计算方法不是“按照整数乘法的计算方法进行计算，积的小数点要和乘数的小数点对齐”，此时，学生产生了“寻找不同的例子来修正原猜测”的欲望。

二、数学论证开启主动学习

数学论证涉及证明与反驳的过程，对发展学生的数学思维、促进主动思考和主动建构具有重要意义。要想培养学生的论证能力，需要把说理变成一种习惯，而要达成这个目标，需将数学课堂经营为学生对话的讨论社群，因为课堂中学生接受的想法是经过学生间相互论证、辩驳、推理达成的共识，而不是决定于教师的权威。

宽松、自由的探究环境中，学生的数学论证过程会经历三个历程：取信自己、取信朋友、取信“敌人”。对于前面遇到的“小数乘小数”问题，学生在主观猜测的过程中产生了困惑，势必会努力扩大题例的范围，通过自学课本、小组交流、集体辩论等方式进入数学论证过程，具体表现为五个阶段。

1.重新归纳。学生凭借视觉直观、知识的前后联系及数学推理找出与前面主观猜测不符的题例，如自学课本发现0.2×0.3=0.06，从前期的学习中可以得到0.8×0.1=0.08等。在这个阶段，学生对题例的选择不会再像前一历程那样有所局限，而是尽可能对直观获取的题例进行拓展，如学生会想到0.8×0.01=0.008或0.08×0.1=0.008等。学生对新的题组进行类比和溯因，初步得出结合具体题例的计算方法，如计算0.3乘0.2，先不看小数点，算二三得六，两个乘数共有两位小数，所以从积的末尾数出两位，点上小数点；而0.8×0.1、0.8×0.01 或 0.08×0.1 都可以用这种方法计算并得出正确结果。

2.建立证据。带着这样新的认识，教师及时干预，组织学生开展小组讨论，学生开始积极寻找证据说服同桌或小组内的同伴，这是一个举例说明和动手操作的过程，学生的方法可能有以下几种：

①用百格图涂一涂，得出0.2×0.3的结果是0.06；

②用单位换算的方法得出0.2×0.3=0.06；

③用乘数的小数点移动引起积的大小变化规律获取结果；

④用计算器计算出结果等。

这一阶段的论证开始有了语言文字、数字资料和表格、图画的形式辅助，学生在小组内形成共识：小数乘法的计算方法是按照整数乘法的计算方法算出结果，再数出乘数一共有几位小数，就从积的末尾数出几位，点上小数点。但对这一结论的认识还局限在特定的题例，尚未推广到一般化。

3.论证依据。我们知道学生的论证并非都是有效的，论述的数学语言也并非都是精确的，难以保证它的合理性。所以，教师要组织全班讨论，目的是制造相互验证各组观点的机会，学生在相互质疑中进行反思，同时为了说服他人会努力寻找范围更为宽泛的、不同类型的题例，实现结论的一般化。如：“1.8×2.34的竖式该怎么对齐？”“200×0.05 的积是几位小数？”

在彼此的质疑声中，学生再回到小组，对有疑惑的题例进行计算和验证。这些问题的提出和解决，以及各小组不断扩大的例题数量，使刚刚得出的结论推广到各种不同形式的问题中，实现了结论的一般化。

4.形成论述。论证进入到这一步，学生已经可以在完成表1的过程中对猜测进行修正，并最终形成完整的数学化表述：计算小数乘法先不看小数点，按照整数乘法算出结果，再数出乘数中一共有几位小数，就在积的末尾数出几位点上小数点。至此，学生基本实现了新知建构。

表1

5.聚焦概念。教师在论证活动的概念化过程中要发挥引导作用，而且要在不同时机扮演不同的角色。为了能聚焦，在概念化的过程中，教师需要提供适当的任务，让学生展开反思和拓展。如在学生已经知道“小数乘小数”的计算方法后，教师给学生提供表2，要求学生填一填，并最终说出他们的发现。

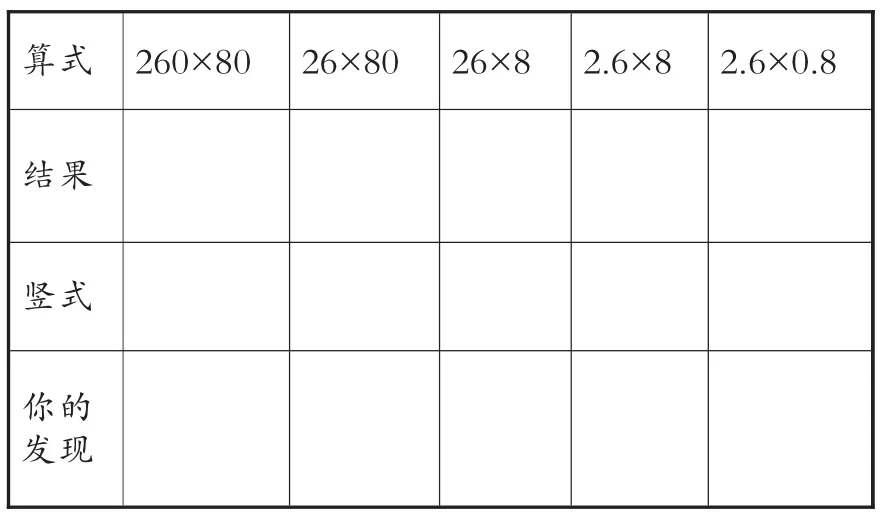
表2

借助这一“支架”，学生将末尾有“0”的整数乘法与小数乘法进行比较，清晰地呈现出概念的形成和发展过程，学生瞬间就为自己刚刚形成的论述找到了强有力的“心理依靠”，并且为后面学习小数乘法的竖式计算奠定了重要的基础。

“重新归纳”是在取信自己，“建立证据”是为了取信朋友，“论证依据”则是取信“敌人”，随后是数学论证的总结（形成论述）和拓展（聚焦概念），将感性的认识进一步提升为理性的抽象和概括。这样的数学论证过程展现在师生、生生互动之间的数学沟通活动中，透过它可以了解学生的数学想法、培养数学推理和概括能力。从主观猜测到数学论证，完整地呈现了学生自主思考、自主建构的学习历程。