基于TIT2FS几何度量的LINMAP方法

彭 颍，毛军军,1b，张凤晓，邹 斌

（1.安徽大学a.数学科学学院；b.计算智能与信号处理教育部重点实验室；2.安徽广播电视大学 教育科学学院，合肥 230601）

0 引言

近年来，模糊理论受到研究者的广泛关注。在模糊的研究中美国控制论专家Zadeh[1]首先提出模糊集合理论，此后研究者在该理论的基础上更进一步的完善和推广。首先模糊集是带有精确定义的隶属函数或隶属度，然而在实际中，有时隶属度仍表现出模糊性，使之很难用一个数值表示，由此提出区间二型模糊集。其次，当人类在描述评价客观事物时，更惯用语言方式。为了更加贴切人类的正常思维及生活方式，进而不同语言评价值的处理方式日益受到研究者的青睐。

目前语言评价值的处理方法主要有以下3种:将语言信息转化为模糊数来计算、使用语言下标处理语言信息、将语言转化为二元语义处理。随着对模糊集理论的探索与研究，第一种方法更受到广大研究者与决策者的关注[2-9]，因而衍生出区间梯形二型模糊集，它能够有效客观的将语言评估转变成数字变量。以区间梯形二型模糊向量与其近似正负理想的几何度量给出拟合指数，再结合区间二型LINMAP方法得到最佳的决策选择，这样既简化计算又合理精确。

1 基本概念

区间二型模糊集的基本概念会广泛应用于本文中，在这部分会做一个简短的回顾，从经典模糊集到更具广泛性的区间二型模糊集以及基于区间二型模糊环境下的区间二型梯形模糊数，它将会用于本文的决策规划中，是本文探讨的根本。

1.1 区间二型模糊集的基本概念

定义1[9]：设X为论域，则定义在X上的二型模糊集A表示[0， 1]}，fx()

u∈[0，1]}。其中Jx表示论域X中元素x对于A的主隶属函数，u是Jx中的某一个主隶属函数值；对全部的称为x关于A的次隶属函数。

定义2[9]：设A是论域X上的二型模糊集，若对∀u∈Jx有，则A称为论域X上的区间二型模糊集，表示为:。这里μA()x是x对A的主隶属度。

1.2 决策环境下的区间梯形二型模糊集

区间梯形二型模糊集是区间二型模糊集的特例，考虑多准则决策问题时，本文用区间梯形二型模糊集来表示评估等级。其中定义为决策的m个选择，让x1，x2和xn表示c1，c2和cn的相应的数值。集合C可以分成CI和CII两个集合，CI表示利润标准，CII表示成本标准，CI∩CII=∅，CI∪CII=C。

定义3[10]：对任意非负梯形模糊数Aij(Aij∈[0，1]) ，和μAiU()

x分别为Aij的下隶属函数和上隶属函数(xj∈X)，区间二型梯形模糊数Aij表示为：

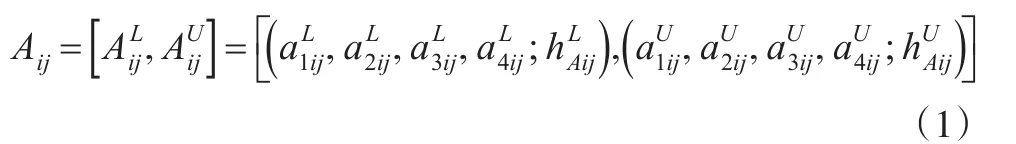
令wj是每个标准cj∈C的权重，其满足标准化条件，且。设未知的标准C的权重向量为，需要借助后面提出的区间二型模糊LINMAP方法解得。

2 区间梯形二型模糊环境下的不确定性几何度量

2.1 区间二型梯形模糊向量

区间二型模糊集是区间一型模糊集模糊化的结果，即对一般集合描述事物的再一次模糊化，这是区间二型模糊的鲜明特征。现在考虑是否以向量形式将本文中的区间梯形二型模糊集表示出来，以下给出定义及说明。

定义4：从非负区间梯形二型模糊数Aij中任取两个模糊数，用Af、Ag表示：

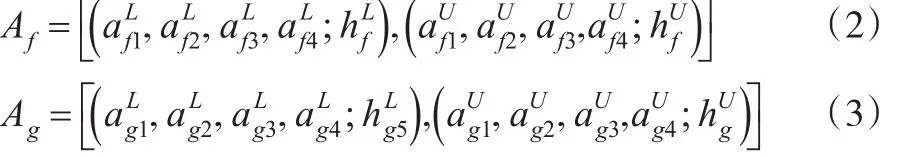
将其化为模糊向量，记为：

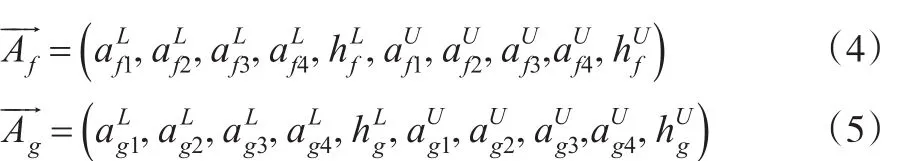
因为区间二型模糊数是对一型模糊数的进一步模糊化，为了保证区间梯形二型模糊数的有效性，区间梯形二型模糊数在转化为模糊向量时不改变其数值，将其整体视为向量。模糊数中各项均为大于0小于1的数，此证明见文献[10]。

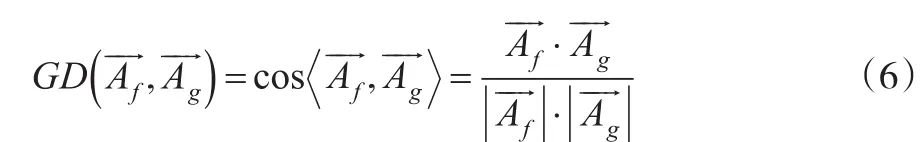
图1 模糊向量投影

2.2 区间二型梯形模糊向量的近似理想

区间二型梯形模糊向量近似理想的引用，一是为了说明当区间梯形二型模糊数转化成向量时其几何夹角问题，二是为了引出本文对区间梯形二型模糊向量给出排序的关键。若将正负理想用于区间梯形二型模糊数中，则得到的正负理想并非是区间梯形二型模糊数，因此采用文献[10]提出的近似正负理想并向量化。

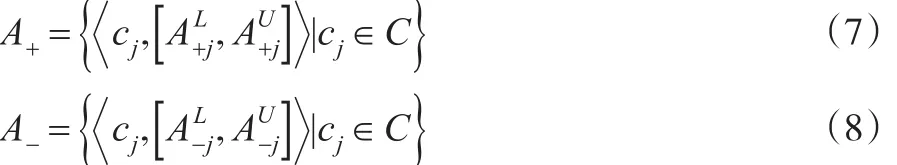
在标准cj∈C下，由式（7）、式（8）得近似正负理想向量和具体表示下：

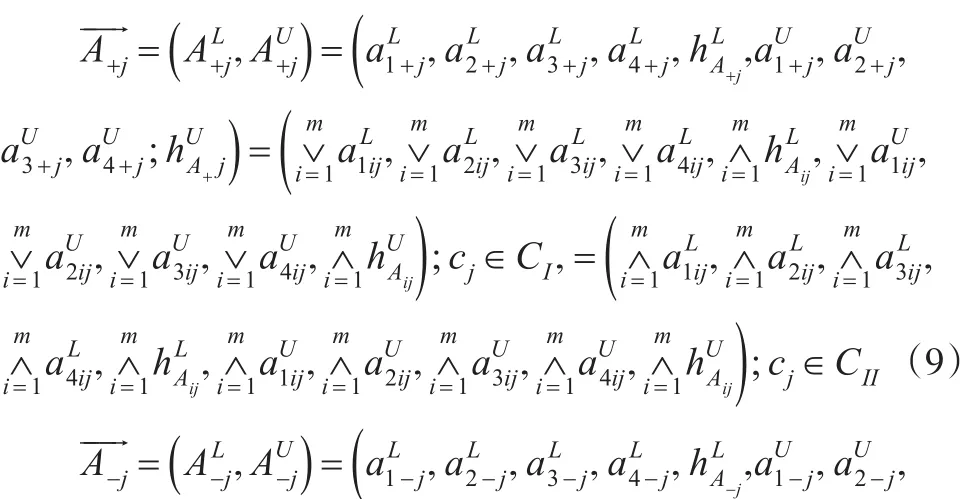
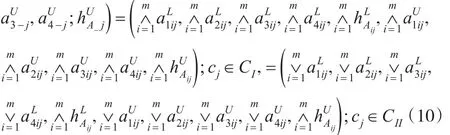
有了二型梯形模糊数的近似正负理想，可以得到在某标准下的近似正负理想的模糊数，由定义5将一组二型梯形模糊数转化为向量后，可以知道这一组模糊向量的近似正负理想必将这组模糊向量包含其中，因此可以通过近似正负理想的向量得出这组模糊向量的夹角范围及其性质。

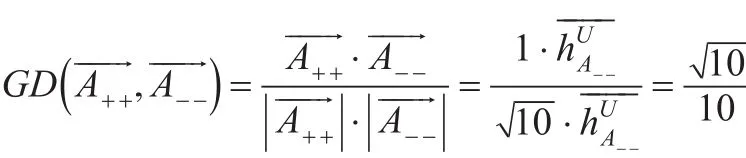
当一组模糊数的近似正负理想向量相等时，此时向量夹角最小为0同时余弦值最大，有

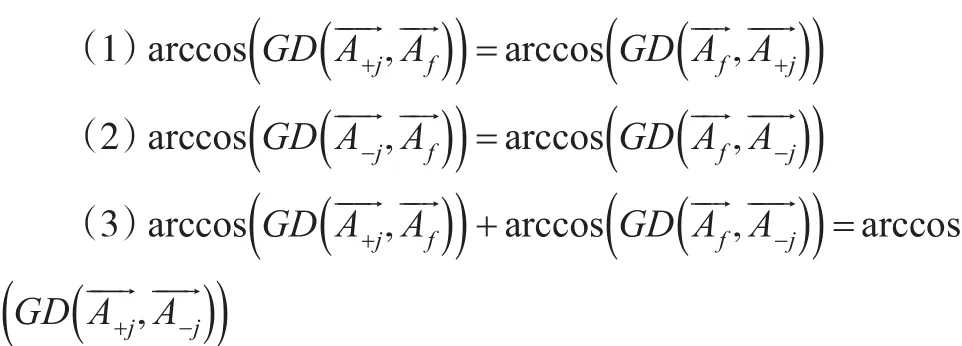
证明：由余弦本身的特征可知（1）、（2）显然成立；欲证（3）将向量做几何投影到平面oxy上，依据空间向量投影公式和反余弦函数，（3）显然成立。

3 区间二型模糊LINMAP方法

3.1 拟合指数

在许多前人研究中，大多使用所选择方案与其正负理想之间的距离，作为组成贴近度系数的成分。为了得到更为合理精确的贴近度系数，有时会通过计算对不同距离公式进行比较，从而产生大量复杂的运算，如文献[10]中的闵可夫斯基距离公式。为了区分模糊数的贴近度，本文给出基于区间梯形二型模糊向量的拟合指数，设为非负区间梯形二型模糊向量--Aij，在标准cj下选择zi的拟合指数公式为：

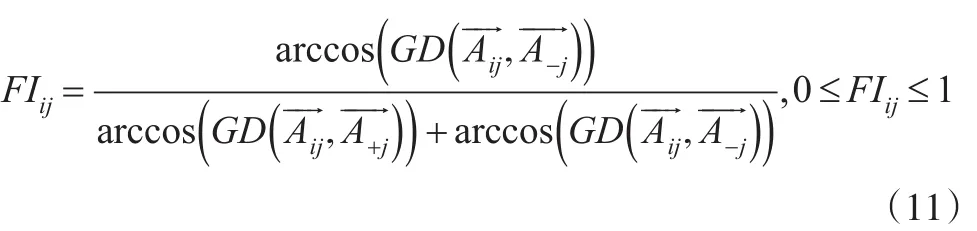
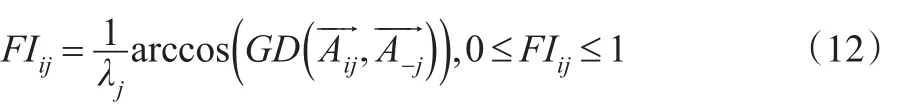
3.2 最优模型

基于区间梯形二型模糊向量解决多准则决策问题的LINMAP方法，文献[10]给出了区间二型模糊LINMAP方法，基于区间梯形二型模糊向量我们对其作出改进。

定义7：假设Ω为一系列表示选择方案偏好关系的有序对集合，在标准cj∈C下的未知权重向量是w=(w1，则选择方案zi∈Z的综合拟合指数WIi表示为：

上文提到当决策者所表达的偏好排序与计算的排序不一致时，需要尽可能减小这种不一致性。现假设zf偏好于zg，相应的应满足FIf≥FIg。依照这种规则定义Ω中一致性系数和不一致性系数公式如下：

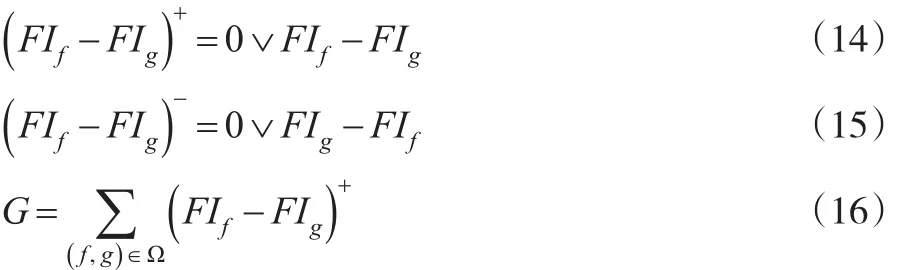
为Ω中所有有序对一致性系数之和;

为Ω中所有有序对不一致性之和;

G-B≥η为决策者最低接受限度，以此建立最优模型，为了使不一致系数B最小，则最优模型构建为:

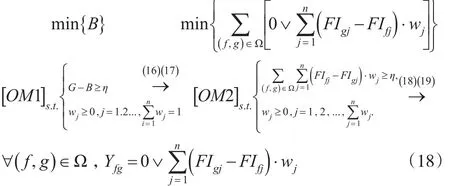
显然Yfg≥0，即，此时有：

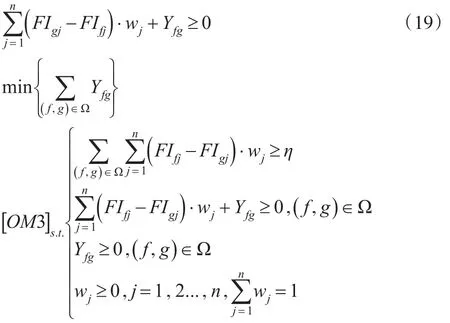
最后，通过区间二型LINMAP方法解出更为合理的最优权重-wj，其综合拟合指数为：

对∀zi∈Z依据对m个选择项进行排序，从中选择数值最大的，即为决策者的最佳选择。

4 算例比较

参考文献[10]的算例，一个化学药品和光纤公式的高管，希望选择合适的供应商，以减小供应链的风险和不确定性，最后从中选出5个供应商。

第二步：供应商候选人的语言评估等级（见表1）构建区间梯形二型模糊数Aij，并转化成区间梯形二型模糊向量。

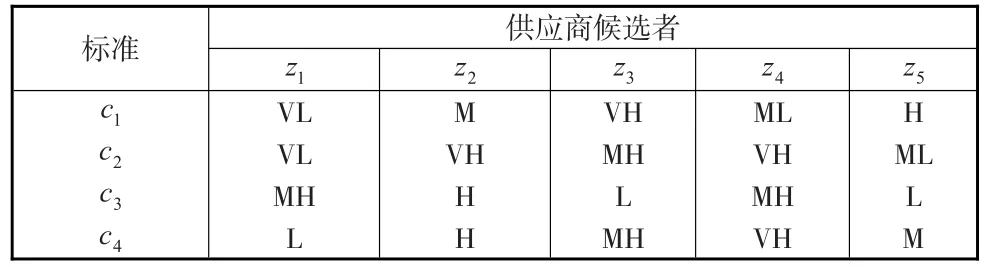
表1 语言评估等级

第三步，假设决策者对这5个供应商提供的成对比较信息为：

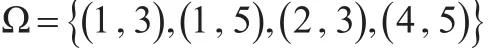
第四步，构建标准cj∈C下的近似正负理想模糊向量；计算拟合指数FIij：

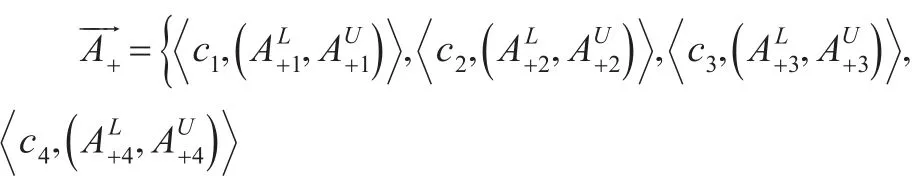
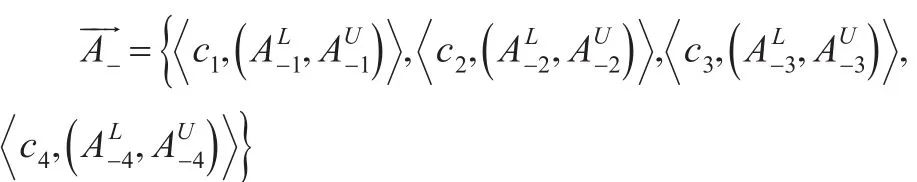
得到近似正负理想的区间梯形二型模糊向量。应用式（11）将基于上面所求得的模糊向量做拟合指数的计算。如表2所示。

表2 拟合指数

第五步，假设决策者可接受最低限度η=0.3，w=(w1，w2，...，wn)为未知权重，满足wj≥0，j=1，2，3，4 ，序对 Ω=，应用线性规划模型，得：

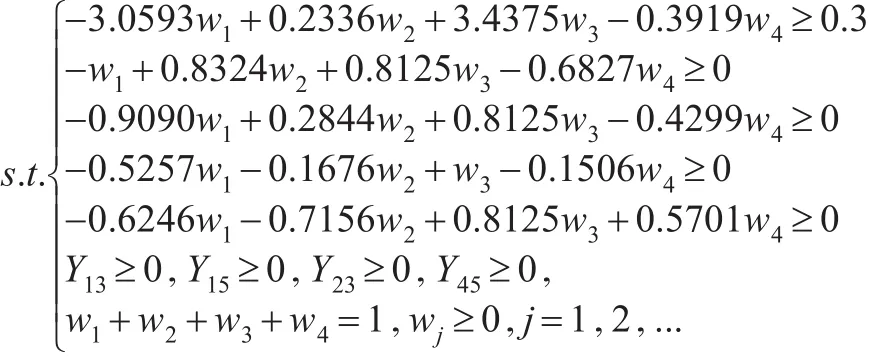
第六步，应用解得的wˉ，应用式（15）计算综合拟合指数如下：

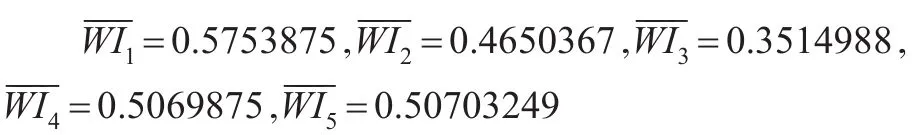
5 结论

本文给出了区间梯形二型模糊向量的定义，及相关性质的证明。在此基础上引出模糊向量的近似正负理想，利用区间梯形二型模糊向量与其近似正负理想之间的夹角关系，提出拟合指数和综合拟合指数。以往选择距离公式计算拟合指数，有时需要比较哪种距离公式更为合理精确，增加了计算量和复杂程度。本文提出的拟合指数公式简化复杂的运算，同时保证了其结果的合理精确性。最后使用区间二型LINMAP方法，对方案进行排序得到最优方案。