竞争风险下右删失数据的剩余寿命分位数回归预测

高 伟，冯海林

（西安电子科技大学 数学与统计学院，西安 710126）

0 引言

涉及医学、工程等领域的可靠性研究中，剩余寿命分位数是做出相关决策的关键指标[1]，它对寿命分布的尾部特征性依赖性较小，且在偏态分布下具有鲁棒性的特点，能较为全面地刻画分布特征。右删失数据是一种常见的数据类型[2]，具有非对称和偏态分布性，而剩余寿命分位数对此类数据有较好的表现[3]。竞争风险数据在经典生存分析中极为重要，它由个体面临失效时间跨度、导致失效的终止事件等多种潜在结局产生，其中潜在终止事件被彼此之间称为“竞争风险”事件。

在剩余寿命分位数的预测中，由右删失数据的分位数回归方法得到的结果较准确。分位数回归方法被Koenker[4]首次引入，被Ying等[5]、Gelfand等[6]、Wang等[7]进一步推广；在竞争风险数据类型下，Jeong和Fine[8]进一步提出了对剩余寿命分位数推断的两样本检验统计量。但这些方法都忽略了协变量对预测的影响。尽管Jung等[9]在右删失数据下构建了协变量对剩余寿命分位数影响的半参数估计模型，但其中的协变量被考虑为固定的。实际上，动态协变量对剩余寿命的预测也有显著影响[10]。目前，尚未有动态协变量对剩余寿命预测影响的研究。

本文基于竞争风险下右删失数据，建立了剩余寿命分位数回归模型，得到了剩余寿命分位数和动态协变量之间的函数关系，证明了提出的估计量的渐近性和一致性。数据仿真和实例分析验证了所提出方法的准确性和有效性。

1 符号和定义

用T表示个体的失效时间，C表示删失时间，即从观测开始到个体删失的时间，令Yi=min(Ti，Ci)，定义示性函数 δi=I(Ti≤Ci)，用 ε∈(1，2，…，K)表示失效原因，令ηi=δiε=I(Ti≤Ci)ε。通常把影响个体失效时间的重要因素称之为协变量，记W∈R(p+1)为固定协变量向量，即不随时间变化，Z∈R(p+1)为与时间相关的动态协变量向量，令U=(W，Z)。假定失效原因为k(k=1，…，K)的累积发病函数为Fk(t|U)=Pr(T≤t，ε=k|U)，它表示给定协变量U 时，观察到失效原因为k的概率。记在t0时失效原因为k的剩余寿命的子分布函数为 Fk，t0(t|U)=Pr(T-t0≤t，ε=k|U，T＞t0)。假定给定协变量U时，删失变量C和(T，ε)是条件独立的。设G0(t|U)=Pr(C＞t，εi=k|U)是删失分布的条件生存函数。另外，记观测到的数据为{(Yi，δiεi，Ui)，i=1，…，n}。

2 基于动态协变量的剩余寿命分位数建模及其参数估计

基于真实数据的分析表明，剩余寿命分位数与协变量之间的关系一般为对数线性关系[11]。设失效原因为ε=k的剩余寿命τ-分位数和协变量之间的关系是对数线性的，即：

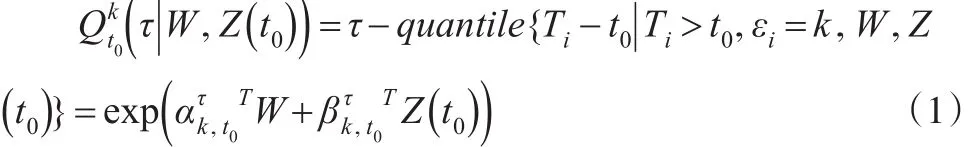
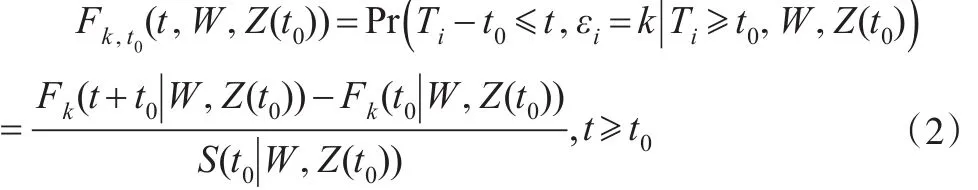
其中 Fk(·)是失效原因为 ε=k 的CIF ，S(·)是所有原因的生存函数。

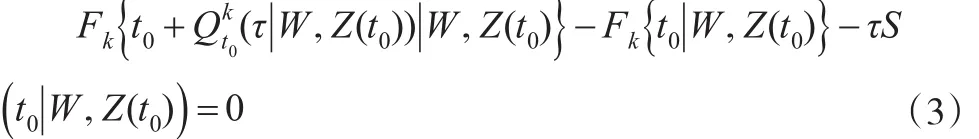
由式（3）得，给定协变量信息下，失效原因为ε=k的τ-分位数函数表示为：

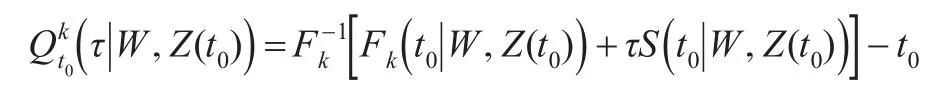
由于在时间t0时τ-分位数函数是CIF在Fk(t0|W，时的逆，因此在t0时，Fk(·)和 S(·)都会影响τ-分位数。令，其中是给定协变量信息时失效原因为ε=k的累积风险函数，ζ即观测时间的最大值。于是，τ-分位数存在的必要条件是，即ζ，因此t0被约束。

由式（1）和式（3），知：

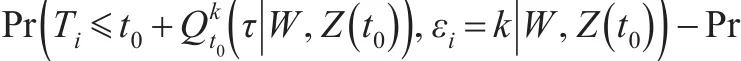
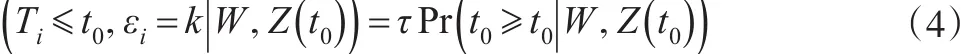
假设 (Ti，εi)和Ci是条件独立的，则式（4）的左边第一项等价于：

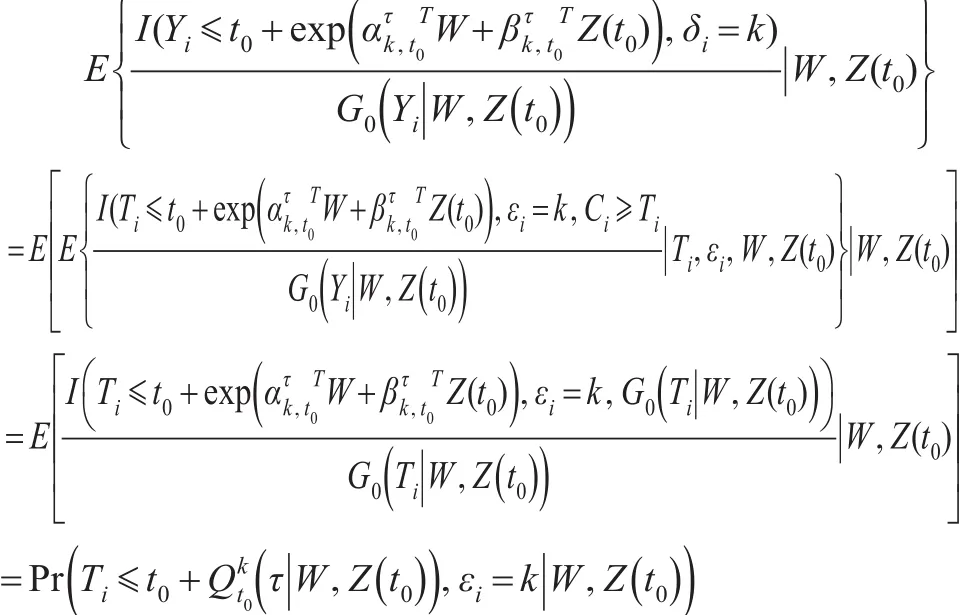
而式（4）的左边的第二项等价于：

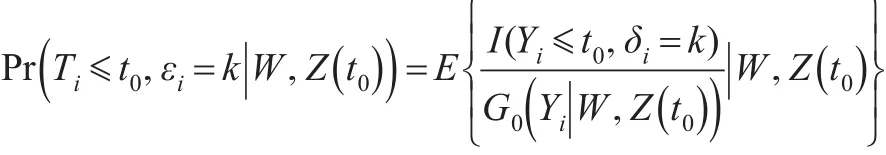
因此，式（4）即为：

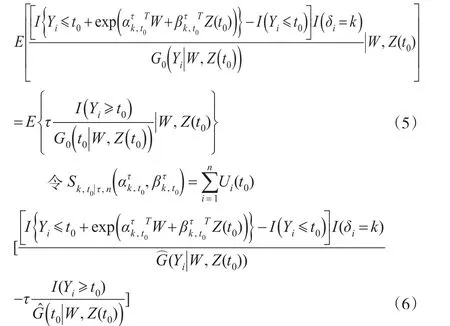
其中G(t|W，Z(t0))是给定协变信息时删失分布的条件生存函数的Kaplan-Meier估计值[9]。于是：

3 仿真模拟

假设竞争失效原因ε∈{1，2}，本文仅对类型1事件感兴趣，即ε=1，通过数值仿真来检验所提出方法在有限样本下的表现。考虑一个简单的情形：

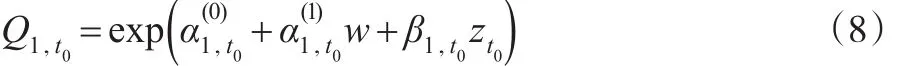
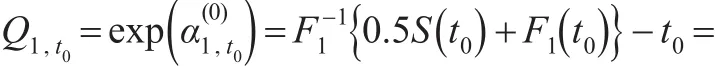
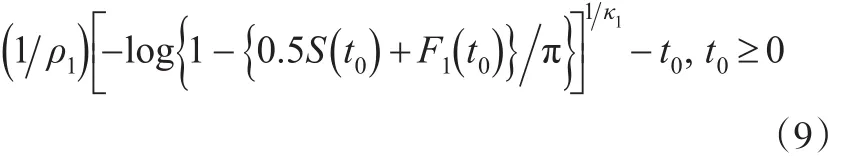
t0=0时假设 ρ2=0.4，κ1=κ2=1.5，。 用产生类型 1 事件的事件时间真值产生类型 2事件的事件时间真值，其中，删失时间C～UNIF(0，c)，其中c为控制删失比例的常数，观察到的生存时间Yi=min(Ti，Ci) ，其 中假设 w～Bernοulli(0.5)，是不随时间变化的协变量，zt0是随着时间变化的协变量，这里采用文献[10]中的协变量表达式zt0=

本文估计了在删失比率分别为0、10%、20%、30%的情况下，τ-分位数分别为0.3、0.5且时间t0分别为0、0.5、1、1.5时回归参数估计的经验偏差（Bias）、经验标准差（SD）、平均标准差（SE）和95%Wald型置信区间的经验覆盖率（CP）。

表1 t0=0，0.5，1，1.5时，真值回归参数1.40，1.29和的经验估计

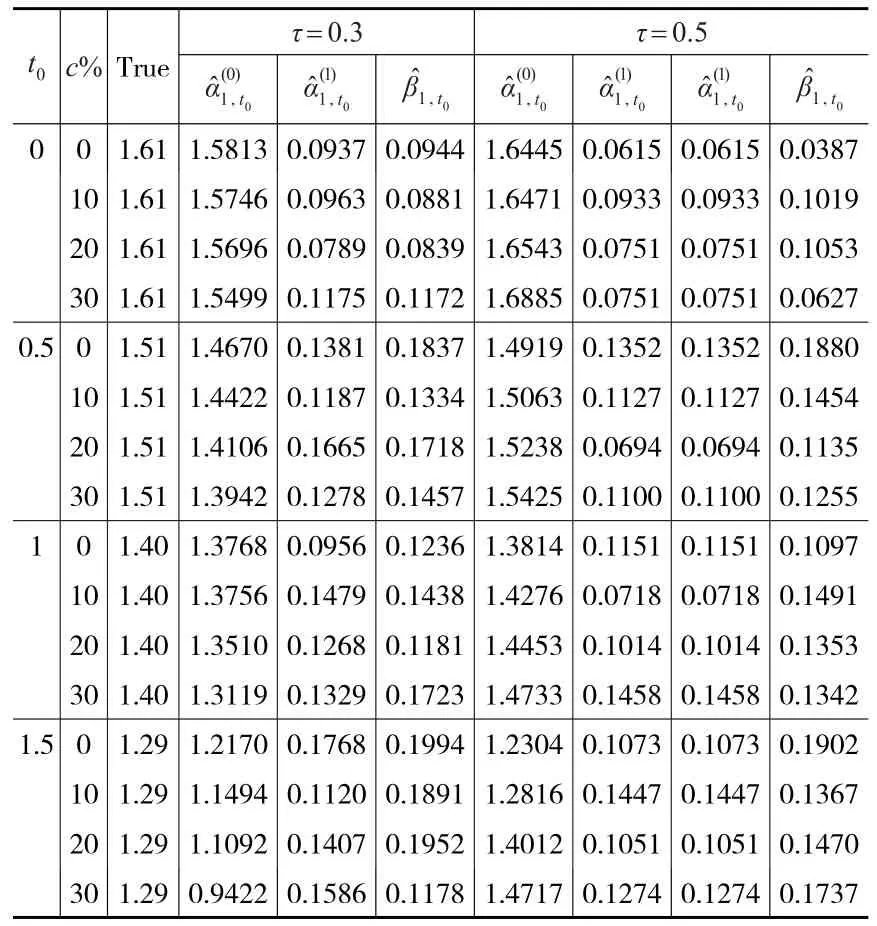
表1 t0=0，0.5，1，1.5时，真值回归参数1.40，1.29和的经验估计

注：c%表示删失比例。

t0 0 c%β1，t0 1，t0 β1，t0 True 1，t0 1.5 1，t0 1，t0 α(1)0.5 0.0937 0.0963 0.0789 0.1175 0.1381 0.1187 0.1665 0.1278 0.0956 0.1479 0.1268 0.1329 0.1768 0.1120 0.1407 0.1586 α(1)10 20 30 0 10 20 30 0 10 20 30 0 10 20 30 τ=0.3 α(0)1.61 1.61 1.61 1.61 1.51 1.51 1.51 1.51 1.40 1.40 1.40 1.40 1.29 1.29 1.29 1.29 τ=0.5 α(0)1 0 1.5813 1.5746 1.5696 1.5499 1.4670 1.4422 1.4106 1.3942 1.3768 1.3756 1.3510 1.3119 1.2170 1.1494 1.1092 0.9422 α(1)1，t0 0.0944 0.0881 0.0839 0.1172 0.1837 0.1334 0.1718 0.1457 0.1236 0.1438 0.1181 0.1723 0.1994 0.1891 0.1952 0.1178 1.6445 1.6471 1.6543 1.6885 1.4919 1.5063 1.5238 1.5425 1.3814 1.4276 1.4453 1.4733 1.2304 1.2816 1.4012 1.4717 0.0615 0.0933 0.0751 0.0751 0.1352 0.1127 0.0694 0.1100 0.1151 0.0718 0.1014 0.1458 0.1073 0.1447 0.1051 0.1274 0.0615 0.0933 0.0751 0.0751 0.1352 0.1127 0.0694 0.1100 0.1151 0.0718 0.1014 0.1458 0.1073 0.1447 0.1051 0.1274 0.0387 0.1019 0.1053 0.0627 0.1880 0.1454 0.1135 0.1255 0.1097 0.1491 0.1353 0.1342 0.1902 0.1367 0.1470 0.1737

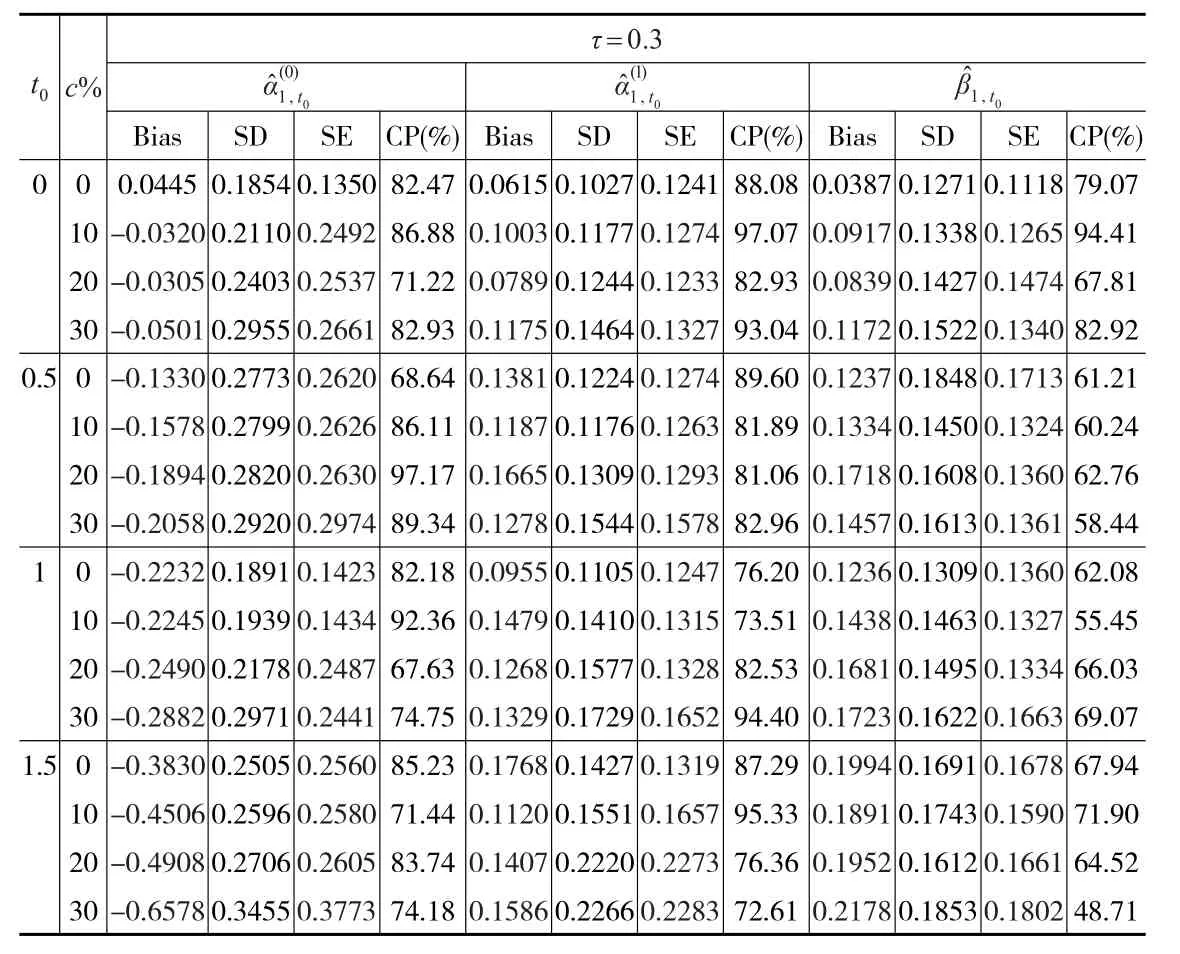
表2 τ=0.3时的Bias、SD、SE、CP

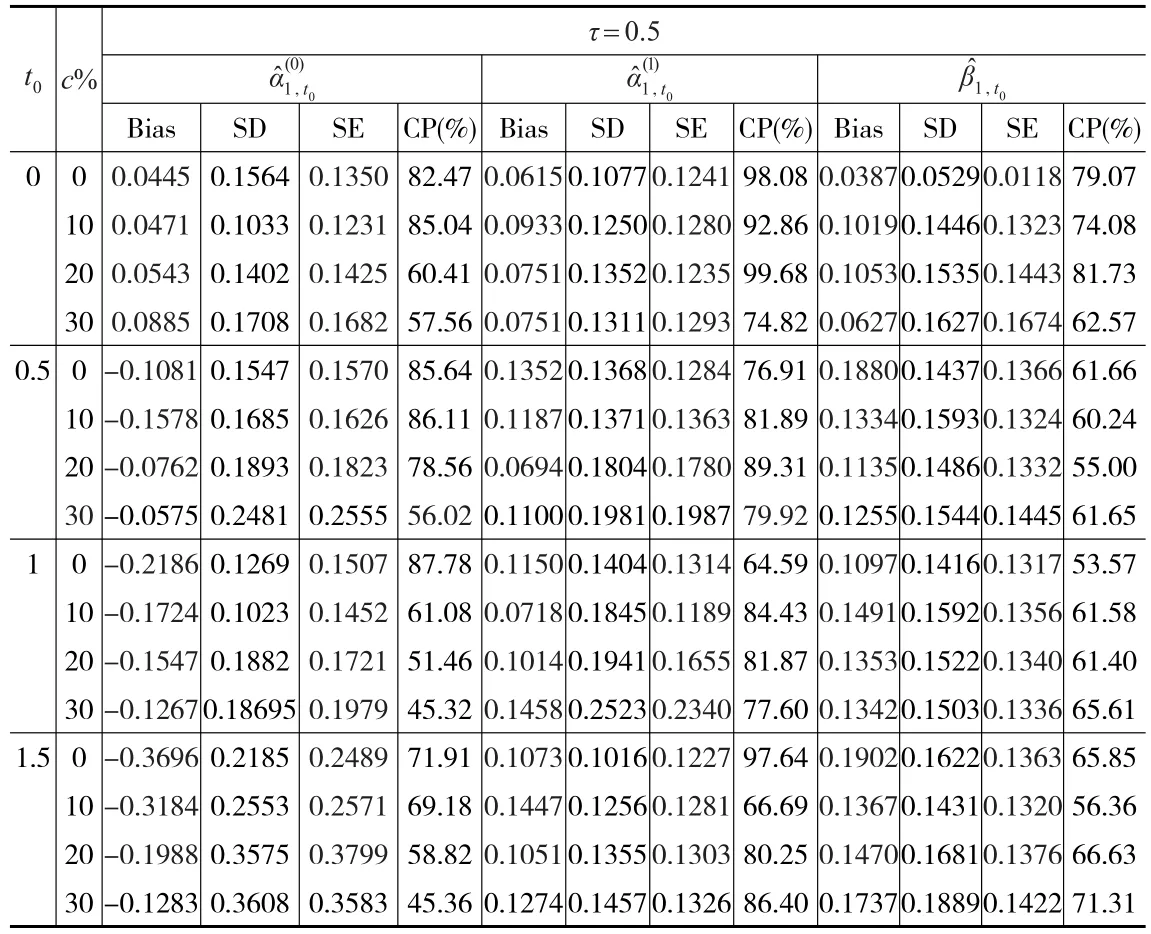
表3 τ=0.5时的Bias、SD、SE、CP

4 实例应用

本文利用美国Channing House数据对所提出的方法进行评估，Channing House是位于美国加利福尼亚州帕洛阿尔托市的一个退休中心，Channing House数据收集并记录了从1964年至1975年7月1日之间成员的有关数据。在这期间，总共有97名男性和365名女性在该中心生活。此外，所有成员进入和离开退休中心时的年龄也被记录。根据记录，发现该数据集属于右删失数据类型，因为结束记录时还有许多成员依旧存活。仅有46名男性和130名女性在研究期间在Channing House退休中心死亡，由此可得删失率大约为61.9%。

本文感兴趣的是成员的性别差异以及进入Channing House退休中心时的年龄和居住持续的时间对生存时间的影响。用w=1表示男性个体，w=0表示女性个体表示人员进入Channing House退休中心时的年龄和居住持续的时间t0。考虑人员的死亡原因为所感兴趣的类型1事件，考虑回归模型对于式（8），在 τ=0.5时利用网格搜索法求解。

表4总结了在t0=0、10、20时的估计值；表5给出参数估计的经验偏差（Bias）、经验标准差（SD）、平均标准差（SE）和95%Wald型置信区间的经验覆盖率（CP），从这些数据中可以看出，估计值有较好的表现；表6表明了性别差异对剩余寿命分位数的影响，在t0取固定值时，女性比男性生存时间更长；表7列出了考虑动态协变量和未考虑动态协变量条件下的剩余寿命分位数的估计值，可以看出成员进入退休中心的年龄和居住持续的时间对剩余寿命有一定的影响，这与先前的预期是一致的。

表4 在t0=0，10，20时的估计值

表4 在t0=0，10，20时的估计值

t0 01 0 20 τ=0.5 α(0)1，t0 4.1963 4.0020 3.7430 α(1)1，t0-0.3948 0.0655 0.0920 β1，t0 0.2421 0.0492 0.0439

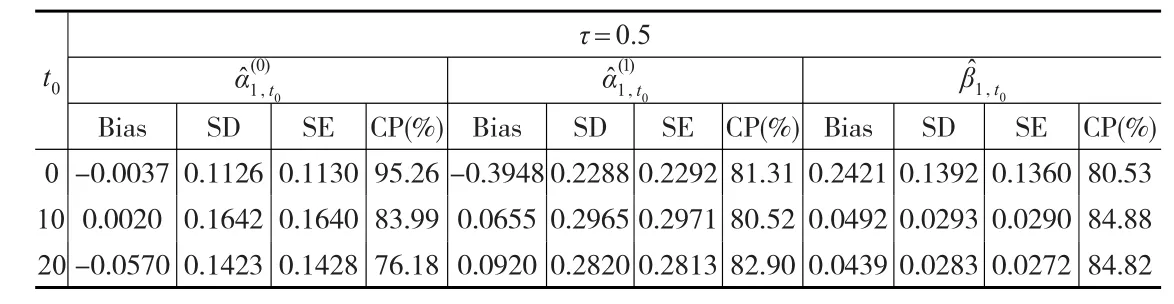
表5 τ=0.5时的Bias、SD、SE、CP

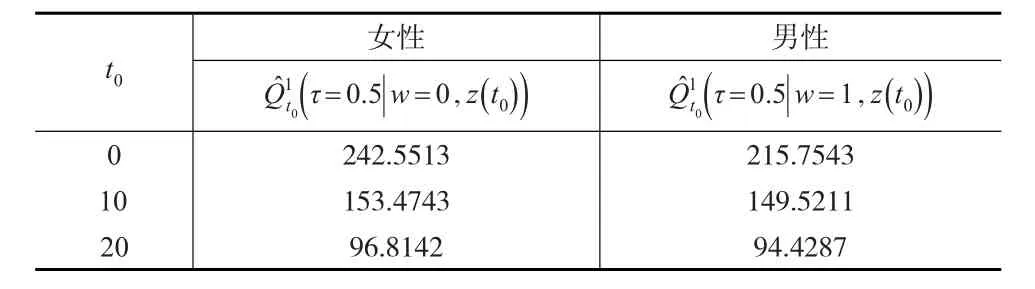
表6 τ=0.5时，性别差异对剩余寿命分位数的影响

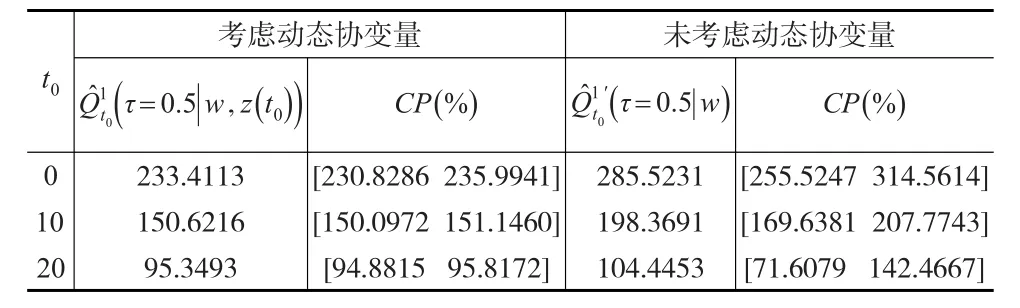
表7 τ=0.5时，两种情形下剩余寿命分位数的估计值

5 结束语

由于在生物医学研究领域，生物数据经常是偏态分布的，分位数回归模型越来越受到研究者的广泛关注。本文提出在竞争风险下右删失数据的剩余寿命分位数回归模型，其主要特点是体现动态协变量与剩余寿命分位数的关系。本文从估计方程中得到估计值，并对其渐进性和一致性进行推导。对模型进行数值仿真，证明提出的估计方法有很好的有限样本性质。最后，将实际数据集应用于模型，充分体现了动态协变量对于剩余寿命分位数的影响。下一步研究，可以尝试研究数据类型更为复杂的情况下，动态协变量对于剩余寿命分位数的影响。