三参数威布尔-几何分布的统计分析

顾蓓青，徐晓岭，王蓉华

（1.上海对外经贸大学 统计与信息学院，上海201620；2.上海师范大学 数理学院，上海 200234）

0 引言

在可靠性分析中浴盆形失效率函数对模拟寿命数据非常有用，大多数产品的寿命周期都呈现浴盆形失效率，但随着寿命数据的越来越复杂，其失效率函数有时也会呈现单调递增、单调递减、倒浴盆形、滚轮形等其他类型的失效率函数，此时常用的寿命分布，例如威布尔分布、对数正态分布等就不能很好地刻画这些寿命数据，于是越来越多的学者提出了一些新的寿命分布，并研究其性质和参数估计问题。Adamidis和Loukas提出了一个失效率递减的两参数分布，称为EG分布（指数－几何分布），讨论其性质和参数的极大似然估计[1]。Coskun提出了一个新的具有递减失效率的两参数分布，称为EP分布（指数－泊松分布），讨论了该分布的各种性质，利用EM算法得到参数的极大似然估计以及估计的渐进方差和协方差[2]。Dimitris给出了估计指数－泊松分布参数的一种EM算法[3]。Rasool和Sadegh提出了一种新的失效率递减的两参数分布，称为EL分布（指数－对数分布），讨论了该分布的性质以及由EM算法得到的极大似然估计[4]。Xie等提出了一种新的模型，称为广义威布尔分布，其有利于模拟具有浴盆形失效率函数的系统寿命，并给出了该分布的参数估计方法[5]。Wu等提出了一个新的具有浴盆或单调递增失效率函数的两参数寿命分布，也可看作是威布尔分布的推广，给出一种简单精确的方法构造形状参数的统计检验，并得到形状参数的精确区间估计[6]。高艳红和周秀轻提出了一种具有单调递增失效率函数的两参数分布，称为RG分布（瑞丽－几何分布），讨论了该分布的各种性质，并利用EM算法得到参数的极大似然估计及估计的渐近方差－协方差阵[7]。

本文将文献[7]所提出的寿命分布作进一步推广，提出了一种新的寿命分布——三参数威布尔-几何分布WG(p，m，β)，研究了该分布的密度函数、失效率函数的图形特征以及该分布的数字特征等，最后利用分位数估计的方法，给出了当形状参数已知时另两个参数的点估计。

1 三参数WG(p,m,β)分布

定义：若非负连续型随机变量X的分布函数F(x)具有如下形式：

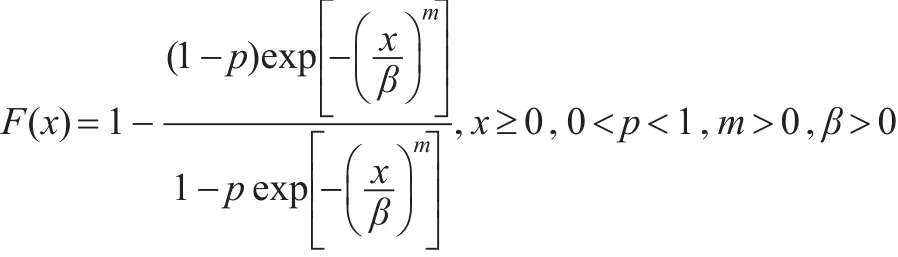
则称X服从三参数威布尔-几何分布，简称为WG(p，m，β)分布。其中m称为形状参数，β称为刻度参数，p称为几何分布参数。

特别地，当 p=0时，即为常用的两参数威布尔分布，所以WG(p，m，β)分布可以看作两参数威布尔分布的推广；当m=2时，即为文献[7]中的RG（瑞利-几何）分布。

假设Y1，Y2，…，YZ为一列独立同服从两参数威布尔分布W(m，β)的随机变量，W(m，β)的密度函数为：。而随机变量Z服从参数为 p的几何分布，其分布列为：P(Z=k)=(1-p)pk-1，0＜p＜1，k=1，2，… ，且 与 Y1，Y2，…，YZ相互独立。记 X=min(Y1，Y2，…，YZ)，此时：

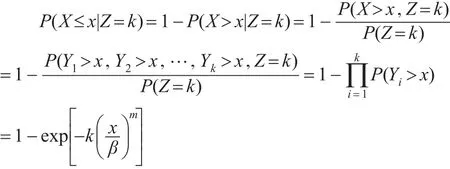
则：

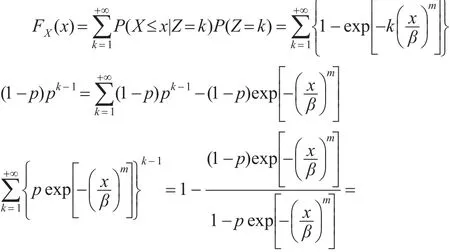
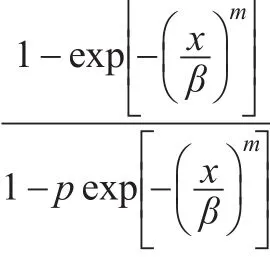
值得一提的三参数威布尔—几何分布WG(p，m，β)是一个混合分布，它是通过将威布尔与几何分布混合在一起得到的。Z可以理解为某种产品中起初存在的同一类型缺陷的个数，Z是未知的，缺陷的出现将导致产品的失效。由于，关于 p是单调递增的，也就是说随着p的增大，该产品中存在多个缺陷的概率在增大，当概率接近于1的时候，该产品中存在的缺陷过多，那么就需要较多的维修费用，可能就没有维修的必要了。

2 三参数WG(p,m,β)分布密度函数、失效率函数的图像特征

定理1：若非负连续型随机变量X服从三参数威布尔—几何分布WG(p，m，β)，分布函数和密度函数分别记为F(x)，f(x)，则（1）当 0＜m≤1时，f(x)严格单调下降；（2）当m＞1时，f(x)先严格单调增加后严格单调下降，即f(x)呈“倒浴盆”形。

证明：易见密度函数为：

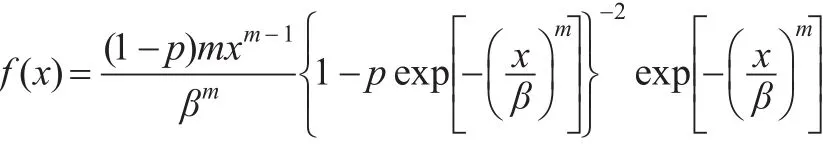
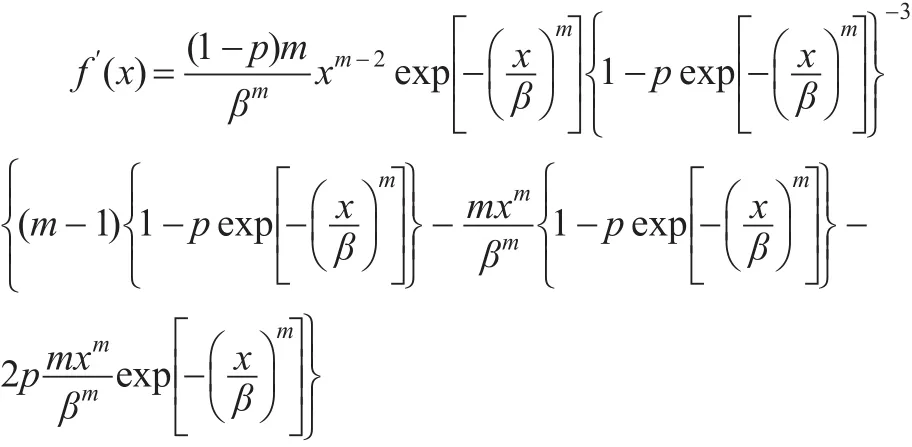
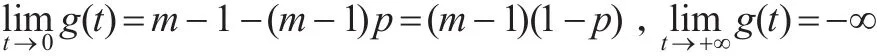
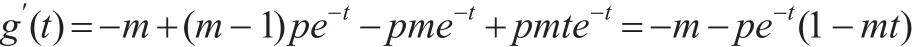
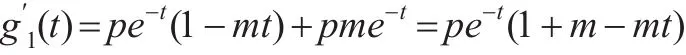
于是当 0＜m≤1时，g(t)＜0，f′(x)＜0，即 f(x)严格单调下降。

当 m＞1时 ，存 在 t0＞0，当 t＜t0时 ，g(t)＞0，f′(x)＞0 ，即 f(x)严格单调增加；当 t＞t0时，g(t)＜0 ，f′(x)＜0，即 f(x)严格单调下降，也就是 f(x)呈“倒浴盆”形。

给定 p=0.5，β=1，m=0.5，1.5，密度函数 f(x)的图像见图1所示。

定理2：若非负连续型随机变量X服从三参数威布尔-几何分布WG(p，m，β)，失效率函数记为 λ(x)，则（1）当 0＜m≤1时，λ(x)严格单调下降；（2）当 m＞1时，存在m0＞1，当1＜m＜m0时，λ(x)先严格单调增加，紧接着严格单调下降，再严格单调增加，即λ(x)呈“N”形；当m＞m0时，λ(x)严格单调增加。

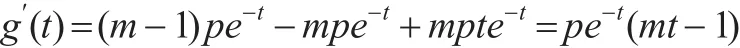
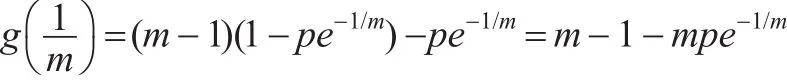
当0＜m≤1时，g(t)＜0，λ′(x)＜0，λ(x)严格单调下降

当m＞1时，令m的函数h(m)=m-1-mpe-1/m，m＞1

令函数h2(a)=1-a-pe-a，0＜a＜1

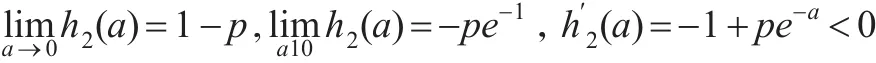
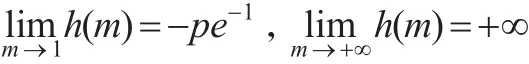
所以，当1＜m＜m0时，h(m)＜0；当m＞m0时，h(m)＞0

由此，当1＜m＜m0时，g(t)的值从(m-1)(1-p)严格单调下降到小于0的数值，再严格单调增加到m-1，即存在 t1＜t2，当 t＜t1时，g(t)＞0 ，λ′(x)＞0 ，λ(x)严格单调增加；当t1＜t＜t2时，g(t)＜0，λ′(x)＜0，λ(x)严格单调下降；当 t＞t2时，g(t)＞0，λ′(x)＞0，λ(x)严格单调增加。此时λ(x)呈“N”形。

当 m＞m0时，g(t)＞0，λ′(x)＞0，λ(x)严格单调增加。

给定参数 p=0.5，β=1，m0=1.3020 ，m=0.5，1.2，1.3，1.4，失效率函数λ(x)的图像见图2所示。

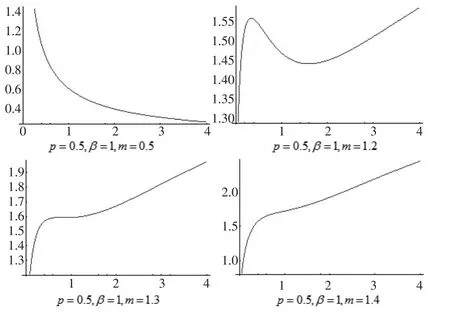
图2 失效率函数λ(x)的图像

为与文献[7]作比较，对RG分布，即取m=2，此时

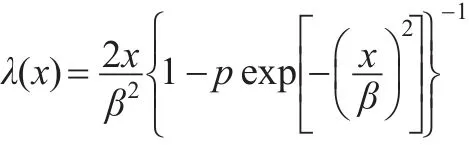
由定理2的证明过程可以看到，对m的函数h(m)=m-1-mpe-1/m，m＞1，由于 h(m0)=0，而 h(2)=1-2pe-1/2，由此，若，则 h(2)＞0，此时有m0＜2，则有 λ(x)严格单调增加。若/2＜p＜1，则h(2)＜0，此时有 2＜m0，则有 λ(x)呈“N”形。

3 三参数WG(p,m,β)分布的数字特征

定理3：若非负连续型随机变量X服从三参数威布尔—几何分布WG(p，m，β)，分布函数与密度函数分别记为F(x)，f(x)，对 k=1，2，…，则：

（1）对 0＜q＜1 ，WG(p，m，β)分布的q分位数

证明：设 WG(p，m，β)分布的q分位数 Mq，则

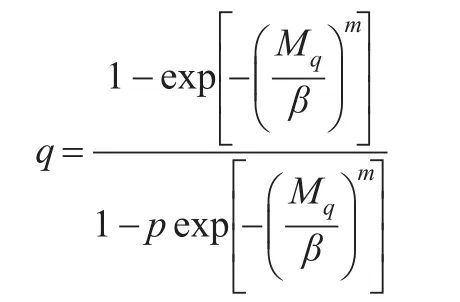
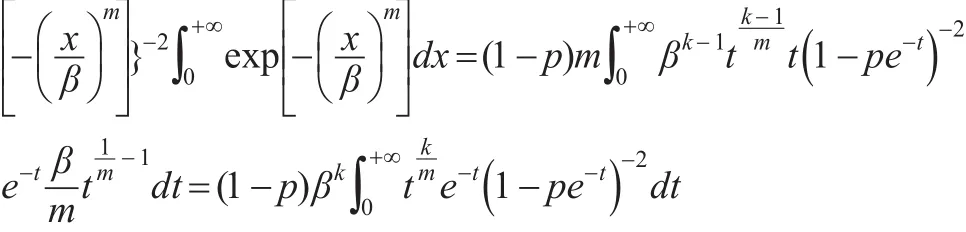
又当|x|＜1时，有如下泰勒展开：

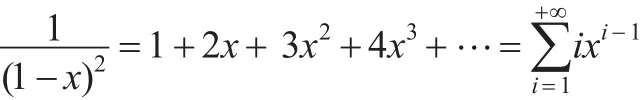
则:

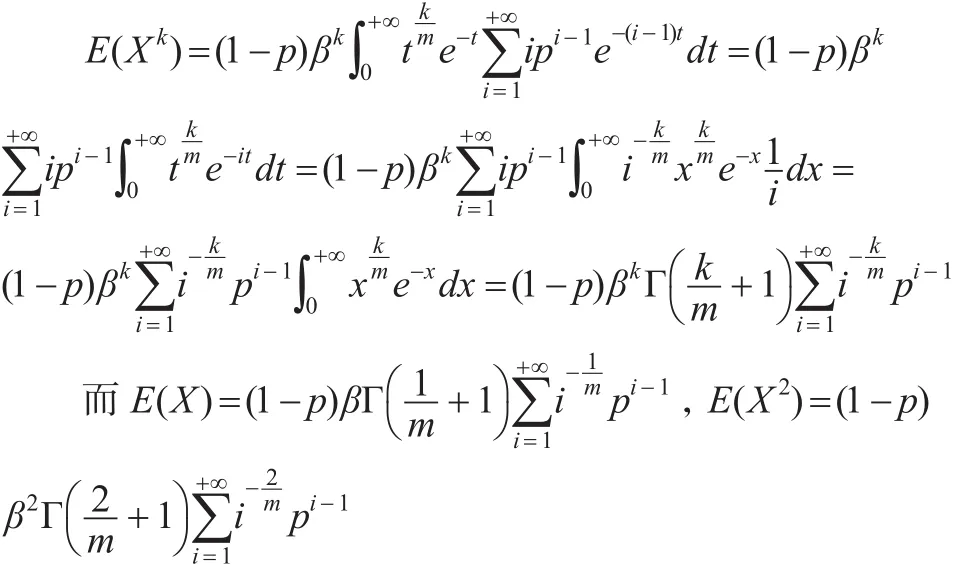
4 形状参数固定时，参数p,β的分位数估计

设 X1，X2，…，Xn为来自总体 X～ WG(p，m0，β)的容量为n的一个简单随机样本，其次序统计量记为X(1)，X(2)，…，X(n)，而形状参数 m0已知。

由定理3可知 WG(p，m0，β)分布的q分位数，于是利用分位数估计的方法，建立如下两个方程：

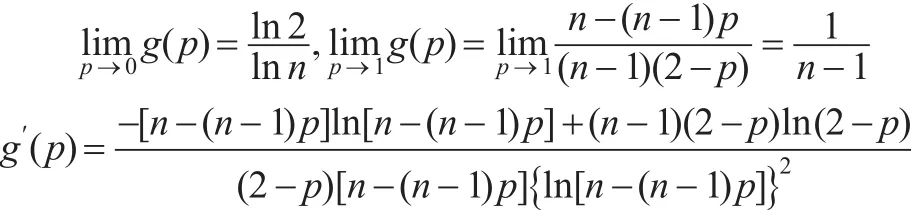
令函数g1(p)=-[n-(n-1)p]ln[n-(n-1)p]+(n-1)(2-p)ln(2-p)，0＜p＜1

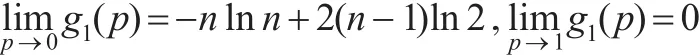
令函数 g2(x)=-xlnx+2(x-1)ln2，x≥2

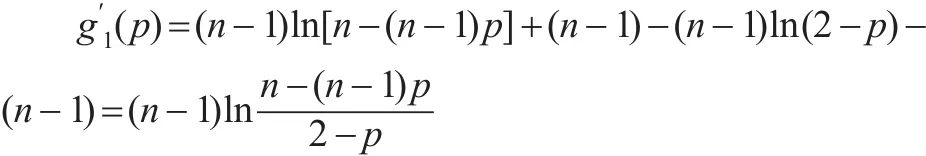
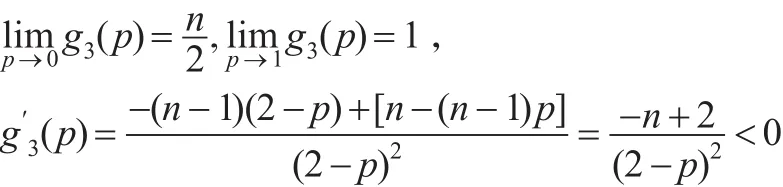
于是有 g3(p)＞1，进而 g1(p)＜0，g(p)严格单调下降，由此可知：当在(0，1)上有唯一正实根。

5 结论

本文提出了一种新的具有单调递减、“N”形、单调递增失效率函数的寿命分布，称为三参数威布尔-几何分布WG(p，m，β)，其密度函数呈单调递减或“倒浴盆”形。该分布的q分位数为，k阶矩为E(Xk)=。此外，当形状参数m=m0已知时，几何分布参数p的分位数估计为方程的根，刻度参数β的分位数估计为