股价崩溃风险对股票超额收益率影响的实证分析

徐 磊，倪 旸

（上海交通大学 安泰经济与管理学院，上海 200030）

0 引言

股市崩溃的特征通常是部分股票价格迅速、大幅下跌，且由于其传染性带动整个市场下跌，甚至蔓延至其他市场。股市崩溃不仅会打击投资者信心，还会损害金融系统稳定性，阻碍金融的资源配置功能。因此研究中国股市崩溃风险，对完善风险资产定价过程、教育投资者价值投资理念、为政府提供政策建议、防范股市崩溃等方面，都有着重要的意义。

资产定价理论一直是金融经济学中最重要的课题之一，资产组合理论、CAPM模型、套利定价理论和期权定价公式的提出，为资产定价理论带来跨时代的发展。但至今为止应用最为广泛的仍为均值-方差理论及在此基础上提出的风险定价模型，其基本逻辑为金融资产存在超额收益是由于额外承受了一定的系统性风险。但是由于均值-方差理论描述样本具有局限性，尤其是在股价崩溃（即股价快速大幅下跌）的情况下，其中涉及的时间维度难以用传统的模型指标来衡量，使得传统模型在市场极端情况下对资产定价描述的准确性不足。崩溃风险作为风险的一个维度，与之前学者们[1-4]提出的风险因素组合在一起，共同构成对超额收益率更为准确的描述。本文选择三因素模型作为参考模型[5-7]，探究崩溃风险在风险资产定价过程中起到的作用。本文的研究贡献在于：第一，根据中国股市的特殊性，筛选出了适用中国股市的崩溃风险衡量指标；第二，在传统均值-方差二维模型中加入时间维度，构造了在中国股市中对股票超额收益率描述更准确的风险因子定价模型，完善了资产定价理论；第三，对中国股市中资产定价过程有效性进行探究，提出以崩溃风险作为指标构建股票投资组合的策略，在实际投资中为投资者提供新的视角；第四，从崩溃风险和资产定价这个全新的视角，研究2015年股市崩溃过程和内在机理，为管理层在完善我国金融管理政策、防范和控制金融风险时提供理论依据。

1 研究设计

1.1 崩溃风险指标选取

1.1.1 国际上的崩溃风险指标

现在国际上被学者们采用过的崩溃风险指标，主要有以下四个：

（1）股价收益偏度（Skewness）

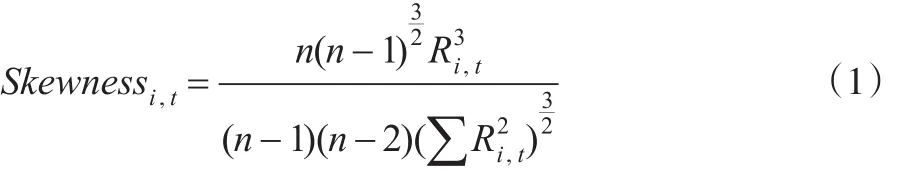
其中，Ri,t表示第i只股票在第t季度内的实际的日收益率，n是第t季度的天数。如果Skewness的数值为负，并且绝对值越大，说明股价收益分布出现极大负值的概率（即出现股价崩溃风险）也就越大。

（2）改进后不含立方的指标（Volratio）

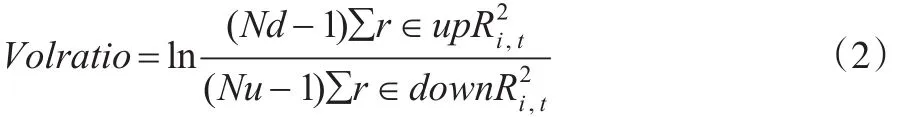
其中，Nd表示上升天数，Nu表示下降天数，而所谓的上升就是当天的回报率高于所有日期平均回报率。假如Volratio的值为负，并且绝对值越大，那么该股票的收益向左偏的情况越明显，即股价出现大幅下跌，股价崩溃的可能性越大。

（3）改进后不含平方的指标（Extratio）

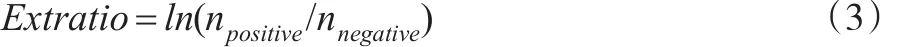
其中，npοsitive表示的是股价回报率出现极端正值的天数，nnegative是股价回报率出现极端负值的天数。而所谓的极端正值，是指在股价收益率正态分布的假设下，Ri，t＞μi+2σi，反之亦然。假如Extratio为负值，且其绝对值越大，则该股票的收益向左偏的情况越明显，即股价出现大幅下跌，股价崩溃的可能性越大。

（4）极大负值出现概率的指标（Crash）

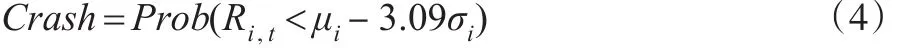
1.1.2 各指标在中国股市的适用性

（1）有效性：比较公式可以看到，公式（1）和公式（2）选取的是所有的观测值，而公式（3）和公式（4）选取的仅仅是一小部分极值，因此对整体收益率分布的描述，公式（1）和公式（2）显然更为准确。

（2）敏感性：公式（2）至公式（4）是对公式（1）的改进，主要在于对极端值的优化，目的在于降低指标对于极端值的敏感性。但是中国证券市场上实施的±10%涨跌幅限制，就已经从制度上防止了股价收益率极值的发生，那么降低对极端值的敏感性就没有很大的必要，反而直接运用公式（1）更为合理。

（3）稳定性：崩溃风险指标的选取，要求不能发生剧烈的波动，指标数据在时间轴上应该反映为一条平滑的曲线。公式（3）和公式（4）的缺陷在于，其对于到底多少算极值这个问题的回答上随意性很强，而且对于这个问题也没有标准答案。极值区间在概率1%、5%、10%的置信度下，崩溃指标会发生非常剧烈的变化，其最终导致的结果也会发生质的改变。

1.1.3 崩溃风险指标

崩溃风险作为个股的非系统性风险，是在均值-方差理论从一阶矩、二阶矩的角度描述信息的基础上，对个股收益信息进行补充性描述。将三阶矩作为崩溃风险的衡量指标是均值-方差理论的进一步拓展，而其他指标的提出则是为了避免极值对三阶矩计算结果的剧烈影响，从而进行降阶的过程。但是降阶后的指标失去了三阶矩的特征，与均值-方差衡量指标之间的独立性难以验证。

因此综合考虑以上因素，在对比有效性、敏感性以及稳定性等特征之后，本文选择公式（1），即股价收益偏度作为个股崩溃风险指标。

1.2 模型构建

经典的资产定价模型可以表示为期望收益率-β形式，其中期望收益率是β的线性函数。其一般形式为：

公式（5）描述的是对非系统性风险进行充分分散化后的投资组合期望收益率，对于未充分分散化的投资组合，其既存在系统性风险，也存在非系统性风险。因此描述该投资组合的期望收益率时应在公式（5）的基础上，加入非系统性风险溢价。其一般形式为：

其中，E是求期望；R是资产的收益率；RF是无风险利率；β是系统性风险的系数向量；λ是系统性风险溢价向量；γ是非系统性风险的系数向量；μ是非系统性风险溢价向量。

Keim（1983）[8]认为股票价格不仅仅与β有关，还与公司的规模大小、杠杆程度、市盈率、市净率等因素有关，这些因素可以视作从不同视角提取的公司信息。Fama和French（1992）[9]发现市值、市净率两个目标就能充分反映公司的不同特质，与市场风险一起有效地描述资产收益率，据此提出三因素模型：

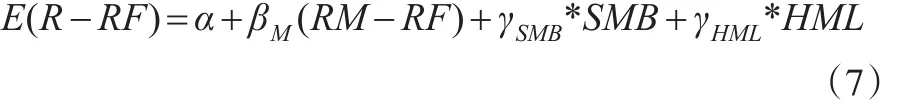
其中，RM-RF是系统性风险溢价，即市场收益率减去无风险利率；SMB是市值因子，即小规模公司与大规模公司股票价值加权收益率之差；HML是市净率因子，即低市净率公司与高市净率公司股票价值加权收益率之差。这些理论模型都是以Markowitz（1959）的资产组合理论为基础，从均值-方差二维视角描述期望收益率。

本文借鉴Fama和French（1996）的三因素模型[10]，在均值-方差二维视角下加入时间维度（即崩溃风险因子），构建模型：

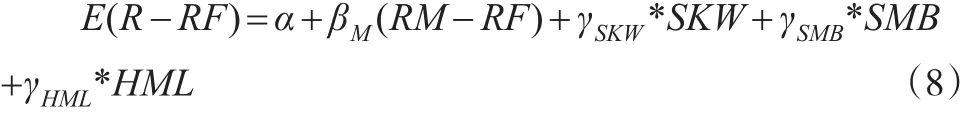
其中，SKW是个股崩溃风险指标Skewness，是非系统性风险从时间维度下的衡量；SMB、HML是FF三因素模型中从均值-方差角度衡量的两个非系统性风险因子。

1.3 数据来源

本文选取上交所、深交所主板市场，中小板，以及创业板的上市公司作为样本，同时将金融类、公用事业类公司及ST公司剔除在外。本文以2011年1月1日至2015年12月31日的市场数据作为样本。数据来源于国泰安CSMAR数据库。

2 实证结果及分析

2.1 崩溃风险定价功能

本文将崩溃风险与市值因素、市净率因素结合在一起，建立5×5×5的股票投资组合，对比组与组之间的价值加权收益是否有显著的差异，从而测定崩溃风险的定价作用，以及该定价作用是否被市值因素和市净率因素所解释。

对于崩溃风险因素，分为L、LM、M、HM、H五组，分别对应于样本数据中Skewness从大到小排序的0%～20%,20%～40%,40%～60%,60%～80%,80%～100%；对于市值因素，将每个季度末所有股票的市值从大到小排列，以20%为一个分位划分为5组，分别记为B、BM、M、SM、S五组；对于市净率因素，将每个季度末所有股票的市净率从大到小排列，以20%为一个分位划分为5组，分别记为h、hm、m、lm、l五组。共构成X.Y.Z，(X∈{L，LM，M，HM，M};Y∈{S，SM，M，BM，B};Z∈{l，lm，m，hm，h})，共5×5×5的股票投资组合。

本文采取如下的模型进行横截面数据回归分析：

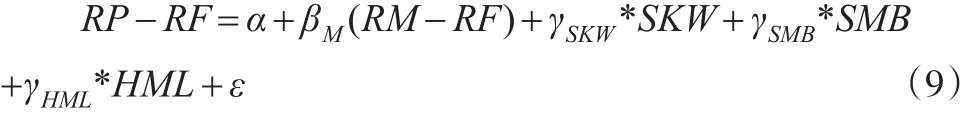
其中，RP指代股票投资组合的价值加权收益率；RF指代无风险收益率；RM指代市场收益率；SKW指代投资组合的崩溃风险因素；SMB指代市值因素；HML指代市净率因素。

市值因素SMB的计算方法为：对于崩溃风险为X(X∈{L，LM，M，HM，M})的 组 ，其 对 应 的

市净率因素HML的计算方法为：对于崩溃风险为X(X∈{L，LM，M，HM，M})的组，其对应的

回归结果如表1所示。

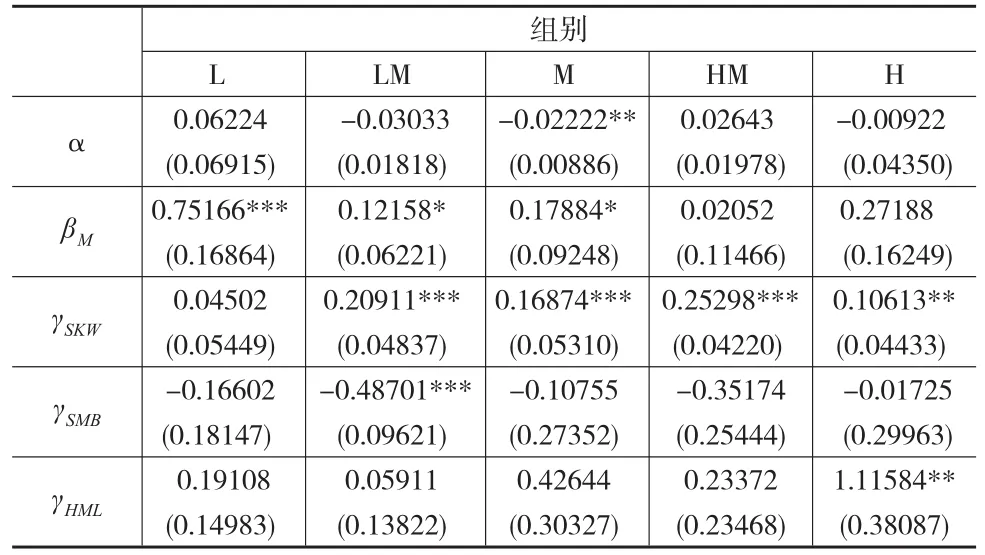
表1 崩溃风险定价功能——模型估计结果

可以看到，γSKW均为正，且在LM、M、HM、H组均显著，这证明了股价崩溃风险在资产定价中确实起到了显著的作用，崩溃风险越大（即SKW为负值且越小），则股票期望收益率越低。γSMB均为负，说明中国股市中同样存在着小市值公司股票收益率高于大市值公司股票的现象；γHML均为正，说明了市净率越高，其股票期望收益率也越高。

这一结论与Boyer等（2010）[4]的研究结果相一致，他们发现美国股市中低崩溃风险组合的收益率超过高崩溃风险组合0.67%/月，收益率与崩溃风险之间的联系是强烈的负相关，认为这是由于投资者偏好于彩票类型的资产，宁愿为了可能出现的超高收益率而去承受高崩溃风险但是低期望收益率的股票。

2.2 2015年股市崩溃过程及机理

股市崩溃的三大特征：主体为整个市场；出现连续、频繁的暴跌；每次暴跌间隔时间短。那么股市崩溃的原因必然不是绝大部分上市公司主体的基本面在短时间内发生了剧烈变化，因而“均值-方差”二阶距模型无法在此期间准确描述资产定价过程。而加入“尾部事件概率”风险偏好的三阶矩模型则能更好地反映股市崩溃期间的投资者对资产定价的过程。

2.2.1 崩溃风险指标处理

本文根据崩溃风险指标的计算方法公式（1），采取滚动法计算单日的崩溃风险，即第i只股票第j日的崩溃风险，采用其第j-t至j-1日的日收益率Rij，代入公式计算得到。采用上述处理方法是由于：“三阶矩”公式的缺点是易受极端值影响，从而带来偏差；而滚动计算的方法缺陷在于容易使数据变得平滑，而掩盖数据特征。股市崩溃期间的特点是极值大量、频繁地出现，将“三阶矩”进行滚动计算，既能满足指标的理论要求，又能克服由于滚动而带来的数据平滑缺点。

本文将样本按市值大小划分为5组，市值前20%的股票构建组合B、市值后20%的股票构建组合S，分别计算两个组合在2015年6月1日至2015年8月31日期间内的日股价收益偏度（Skewness），如图1所示。

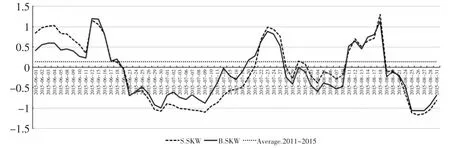
图1 股市崩溃期间大市值股票组合与小市值股票组合的日股价收益偏度

2.2.2 股市崩溃期间投资者恐慌式抛售股票的原因分析

本文运用公式（9）分别计算股市崩溃期间组合S与组合B的崩溃风险指标系数γS_SKW、γB_SKW，与上文正常期间（2011—2015年）的回归系数进行对比，结果如表2所示。

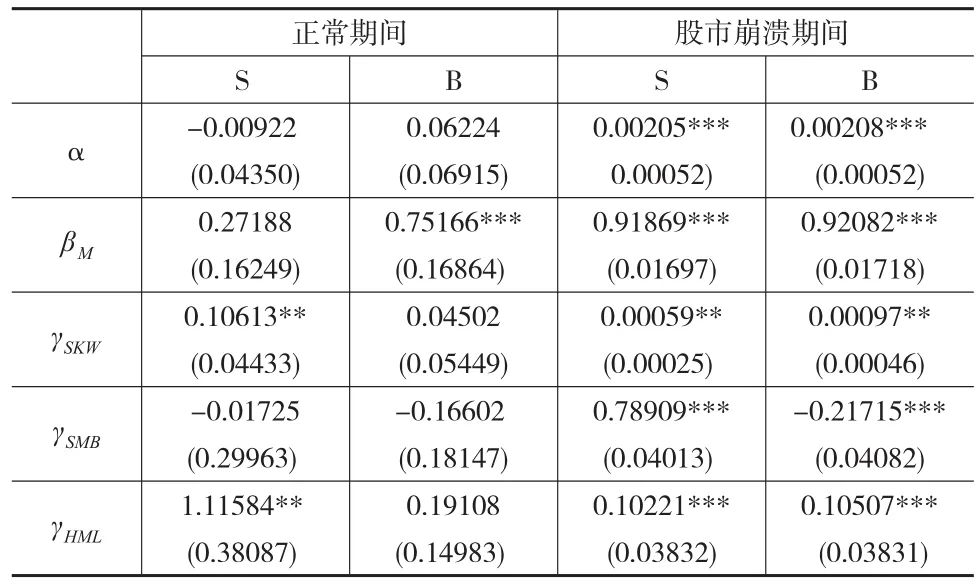
表2 崩溃风险指标系数——模型估计结果

可以看到与正常期间相比，股市崩溃期间两个组合的γSKW仍然为正值，这证实了崩溃风险并没有提供正的超额收益率。两组合的γSKW绝对值均在变小，则表明在SKW（负）值不变的情况下，γSKW*SKW（负）的绝对值在减小，E(R-RF)在变大。这表明在股市崩溃期间投资者对个股要求的期望收益率变高了，对崩溃风险更加厌恶了。因此股市崩溃期间个股崩溃风险变大的情况下，投资者的行为是赶紧抛售，导致许多个股在开盘后很短的时间内就被迅速抛到跌停。

2.2.3 股价崩溃现象会从小市值股票蔓延至大市值股票的原因分析

股市崩溃期间相对风险偏好指标值变大，意味着在大、小市值股票SKW（负）均不变的情况下，相对于小市值股票来说，大市值股票的γSKW*SKW负值更大。这表明相对于小市值股票，大市值股票的E(R-RF)变得更小了，即相对于小市值股票，投资者对大市值股票要求的期望回报率更低，说明投资者相对来说更愿意持有大市值股票。

相对风险偏好的变化决定了投资者在抛售过程中，对大、小市值股票抛售的先后顺序，但其并不是充分条件。因为这只解释了投资者在满足其抛售股票需求的过程中，采取的策略是优先抛售小市值股票，并不能说明在抛售小市值股票后就会去抛售大市值股票。

崩溃风险对应现实中的影响因素有“尾部事件风险偏好”“流动性”。在尾部风险偏好不足以解释的情况下，很可能是投资者对流动性的需求，导致了崩溃现象蔓延。一般来说，对流动性的需求主要体现在机构投资者身上，因此本文选取国泰安CSMAR数据库中“大笔交易”作为股市崩溃期间机构投资者的流动性需求衡量指标。选取2015年6月1日至2015年8月31日期间的所有A股大笔交易数据作为样本，按市值大小、板块分为四组：创业板市值前50家、后50家；主板和中小板市值前50家、后50家。研究板块内、板块间的大小盘股流动性差异对崩溃风险的影响，实证数据统计结果如图2所示。

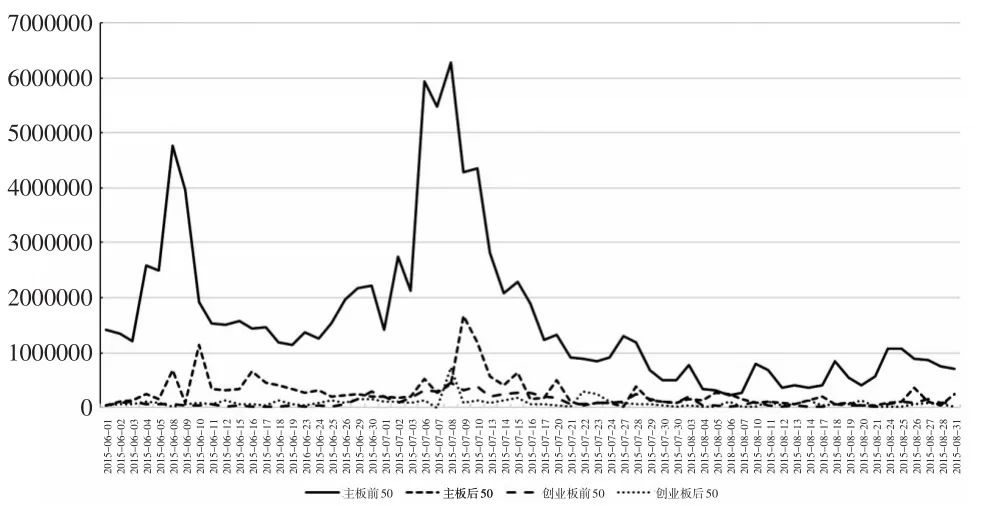
图2 四个组合每日大笔交易总股数指标图

观察板块间组合流动性差异情况，明显可以看到，主板的流动性远远优于创业板。6月中旬股市崩溃，6月24日后大市值股票组合的指标明显上升，反映机构投资者流动性需求开始显现。7月3日后，所有组合的流动性需求指标均大幅飙升，也正是国家资金开始大规模救市的时间点，这是较长期间流动性需求瞬间释放的结果。7月9日后指标下行，表示流动性需求得到缓解，政府救市过程步入尾声。

板块内流动性需求现象也有类似情况。主板内和创业板内，小市值股票组合的流动性需求指标在股市崩溃期间迅速变小，且趋近于0，体现出该类股票提供流动性能力迅速下降。之后大市值股票组合的流动性需求指标开始飙升，表示机构投资者的流动性需求在大市值股票中实现。

以上研究证实了“在股市崩溃期间，机构投资者对流动性的需求无法在小市值股票满足，因而转向大市值股票”这一现象。因此就出现了股市崩溃期间，股价崩溃现象在短时间后从小市值股票蔓延至大市值股票。

2.2.4 崩溃风险视角下股市崩溃过程和背后机理

整个股市崩溃的发生过程及背后机理如下：股市崩溃刚开始时，个股的崩溃风险显著变大，即个股的“尾部事件”概率迅速变大。该段时期，投资者的绝对风险偏好变小，对崩溃风险更厌恶导致了在崩溃风险变大情况下个股的抛售行为。同时投资者的相对风险偏好发生变化，相对于小市值股票，投资者更愿意持有大市值股票，因此投资者在抛售的过程中优先抛售小市值股票。但是由于股市崩溃期间小市值股票大面积跌停、甚至停牌，机构投资者的流动性需求无法在小市值股票满足，因而抛售潮向大市值股票蔓延。

3 结论

本文在传统的均值-方差二维视角下加入时间维度，构造出包含市场收益率、崩溃风险、市值因素、市净率因素四个风险因子的资产定价模型，增加了风险因子定价模型在极端市场情况下描述股票超额收益率的准确性。通过对A股市场2011—2015年的数据实证分析，结果表明股价崩溃风险确实显著地影响了股票的超额收益率，并且崩溃风险与收益率之间是强烈的负相关关系。在2015年股市崩溃期间，个股的崩溃风险显著变大，投资者对崩溃风险更厌恶导致了个股的抛售行为。同时，投资者的相对风险偏好发生变化，导致其在抛售的过程中优先抛售小市值股票。但是由于股市崩溃期间小市值股票大面积跌停、甚至停牌，机构投资者的流动性需求无法在小市值股票满足，因而抛售潮向大市值股票蔓延，最终导致整个股市崩溃。因此，政府应当加强投资者教育、宣扬理性价值投资、同时设立“救市基金”，在必要时为市场提供充足流动性，避免股市因流动性枯竭而发生股市崩溃。