大数据时代数据融合质量的评价模型

李 红，牛成英，孙秋碧，林嘉燕

（1.福州大学 经济与管理学院，福州 350116；2.兰州财经大学 统计学院，兰州 730101；3.福建信息职业技术学院，福州 350001）

0 引言

数据融合是大数据时代发挥数据质量价值的有效手段。来自领域数据库、知识库或者Web开放页面的数据信息被物理地存放在不同系统中，形成数据孤岛。需要把这些割裂的数据整合到统一系统中。如在政府统计工作中，芬兰统计局融合中央人口登记记录、劳动部求职者登记记录、中央和地方公务员记录等行政记录构建人口普查数据库，以解决传统人口普查中调查成本高、普查机构和居民负担重、数据质量低等难题。在Web数据挖掘领域，数据融合的情形更为广泛。如当建立跨领域、跨学科高效的学术信息集成系统时，需要从Web的众多数据源中融合论文发表数、学术专著数、科研项目经费、论文影响因子、参与学术活动等多个指标[1]。大规模、跨领域、多元异构的数据融合深度开发利用遵循的基本步骤[2]：首先根据工作目标选择数据源；然后构建模式映射与记录匹配算法进行数据融合，形成大型统计数据库；最后结合有效的数据挖掘工具，产生统计结果。

显然，大数据时代，数据融合是数据挖掘的基本步骤，大型统计数据库的不确定性来自于数据源的多样性与混杂性。因此，数据融合质量是数据深度开发利用成功与否的关键因素。

1 数据融合质量评价内涵

数据融合一词最早出现在20世纪70年代的军事领域，是利用计算机技术对获得的若干感知数据，在一定的规则下加以分析、综合，以完成所需决策和评估任务而进行的数据处理过程。它的实质是对不同组织形式下的数据进行关联或综合分析，进而选取适当的融合模式和处理算法，用以提高数据质量[3]。

从不同角度看，数据融合质量评价有不同内涵。从数据融合的相关技术和方法看，数据融合涉及融合模式和处理算法。因而质量评价侧重模式选择和处理算法对数据质量的影响。目前计算机科学已率先在这个方面做出不俗成就，相关成果对融合算法、运行环境、信息类型、信息表示、不确定性、融合技术和适用范围都做了对比研究[4-9]。

从数据融合中数据源的涵盖范围看，数据融合质量评价指的是数据源内容的真实性，即误差大小。这里的误差包含两个方面，一是过涵盖误差，二是不足涵盖误差。过涵盖是指不应该被包含在数据源中却出现在数据源中的记录，如通过Web词条搜索得到的虚假记录信息。不足涵盖是指某些记录应该被包含在数据源中却没有被包含，比如某记录没有出现在正确的位置。

有关学者准确界定了涵盖误差的具体分类与影响[10]，如下页表1所示。在传统数据收集方式的影响下，不足涵盖误差出现的可能性较大。然而随着人们社会生活方式的变化、数据收集方式的变化，数据源具有广泛性、交互性和开放性的特点，过涵盖记录出现的可能性在增大。如下页表2中加拿大和澳大利亚的数据显示，即使在传统数据收集方式下，人口普查中的过涵盖误差出现逐年增大的趋势。在Web数据源中，这种趋势更加明显。

因此，本文从数据源的涵盖范围角度出发，构建统计模型测量过涵盖误差，基于此评价数据融合质量，这有利于消除冗余、去伪存真、提高数据融合质量。

表1 涵盖误差的分类与影响

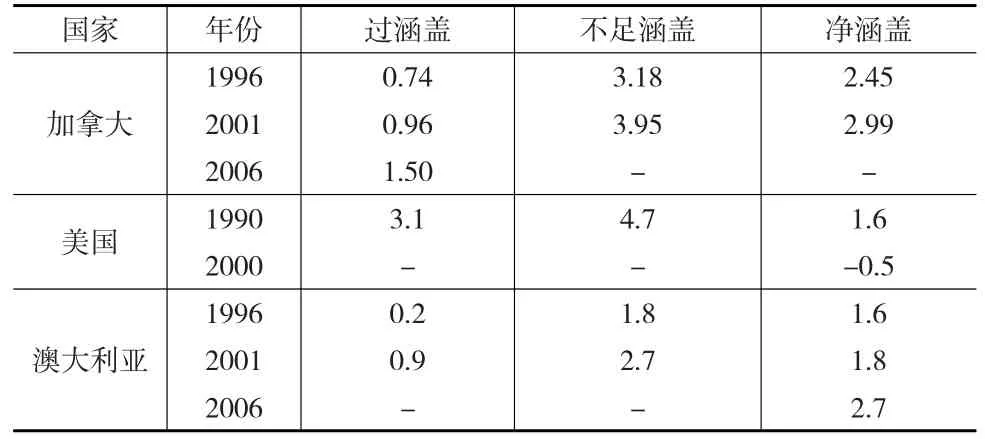
表2 各国人口普查过涵盖、不足涵盖误差估计 （单位：%）

2 基于对数线性与双系统估计的数据融合质量评价模型

2.1 包含过涵盖误差的数据库匹配描述

假设存在两个数据库A和B，如数据库A是公安部门关于人口迁移数据，数据库B是人力资源和社会保障厅城镇失业登记数据。又或数据库A是通过百度热力图获取的某景区某一时间段旅游者信息，数据库B是通过网络词频数据挖掘获取的该景区同一时间段旅游者信息。假定进行数据质量评价之前，数据库A和数据库B已通过记录匹配、文本或人工检查的方式识别数据库中的重复记录。

令T*=T∪A∪B,其中T是目标总体。从T*的定义看，T*可以分解成两部分：目标总体T和非目标总体Tˉ。在总体T*、目标总体T和非目标总体Tˉ下，数据库A和数据库B的匹配结果如表3至表5所示。括号内为对应匹配概率。数据库A和数据库B的样本容量分别为N1、N2。

表3 总体T*中数据库匹配

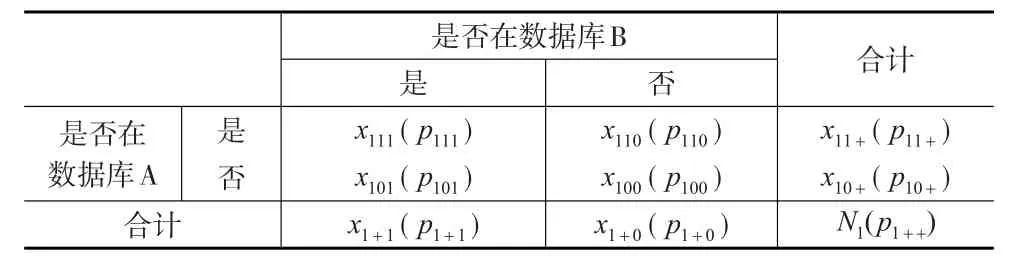
表4 目标总体T中数据库匹配

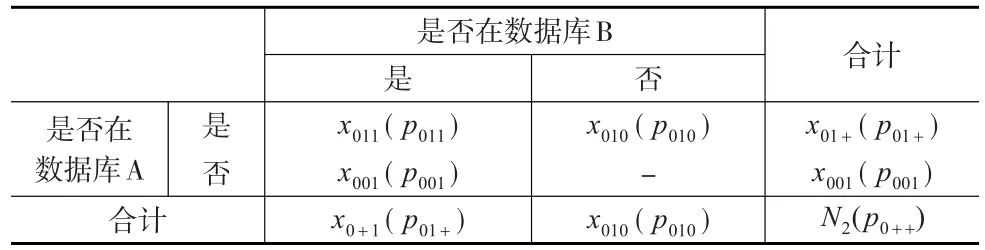
表5 非目标总体Tˉ中数据库匹配

当给定数据库A和B时，x+11、x+10、x+01是已知数。x011、x010、x001是数据库A和数据库B中的错误记录数，且 x+11=x111+x011；x+10=x110+x010；x+01=x101+x001。如果能分解出x011、x010、x001，就可估计数据库的过涵盖误差（已通过记录匹配、文本或人工检查的方式识别数据库中的重复记录，过涵盖误差只与错误记录数有关）。

由表4和表5可得过涵盖误差θab的具体计算表达式：

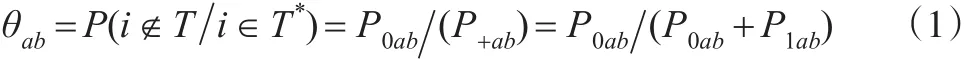
其中 (a，b)∈{(1，1)、(1，0)、(0，1)}。

2.2 抽样调查设计

为估计过涵盖误差θab，设计抽样调查试验S，假定抽样调查试验S满足如下三个条件：

（1）抽样调查试验S只包含不足涵盖误差，因而S中的每一个个体都包含于T中。

（2）抽样调查试验S与数据库A和数据库B的发生是独立的。

（3）抽样调查试验S中每一个个体能与数据库A、B中的元素无错误匹配。

令yab表示S中与数据库A和数据库B匹配下的记录数。如 y11表示集合{x:x∈S∩A∩B}中的记录数。y10表示集合{x:x∈S∩A，x∉S∩B}中的记录数。 y00表示集合{x:x∈S，x∉S∩A，x∉S∩B}中的记录数。

在条件（1）至条件（3）下，可得：

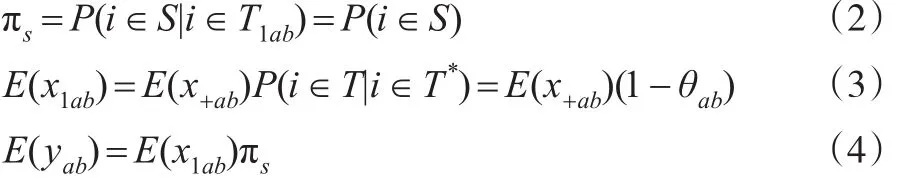
实际中，上述抽样调查试验比较容易产生，如行政数据融合时，可针对研究对象设计分层抽样调查。如旅游数据质量检验时，可对旅游景区做小范围的问卷调查或网络调查。

由表达式（1）至式（4），借助矩估计思想可得：

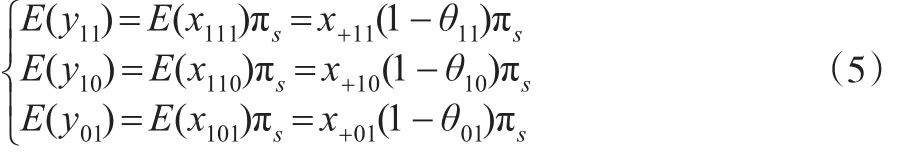
式（5）中包含三个方程，其中，y11、y10、y01、x+11、x+10、x+01已知，θ11、θ10、θ01与 πs未知，因此，还需要构造一个方程估计这四个未知参数。

当 θ11、θ10、θ01与 πs已知时，由式（6）可估计目标总体容量N1：

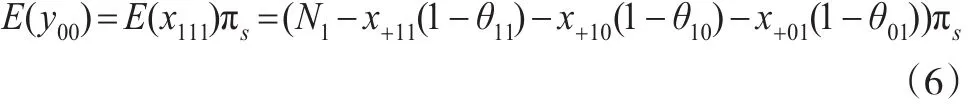
2.3 模型构建与参数估计

目前主要有两种方法可以将列联表数据对数线性模型化。第一种是一般对数线性模型（Log-linear模型），该模型不区分自变量和因变量。所有的变量都被同等地当成“响应变量”来考察他们之间的关系，单元格期望频数是模型中所有变量的函数。第二种是Logit模型。在Logit模型中，某一变量被选作因变量，期望发生比是其他变量的函数，Logit模型非常类似一般回归分析。在数据融合中，数据库A和数据库B不存在因果关系，因此，本文采用一般对数线性模型对列联表数据模型化。

对总体T*=T∪A∪B 建立饱和对数线性模型[12]：

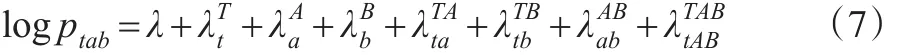
饱和模型（7）将列联表的单元格频数（或频率、概率）表示为对于一般均值λ、每个变量和它们之间相关关系效应的函数。但是饱和模型完全用c个效应代表c个单元格，没有采用简约型。可以通过设定一些效应参数为1（取对数后，效应为0）的方式来构建更加简洁的模型，这类似于回归分析中事先指定一个回归系数等于0。不失一般性，假定三维交叉效应；式（7）中右边各项元素非零，当且仅当元素下标全为1时。同时，由于p000=0，常数项λ=0。因此，可得：

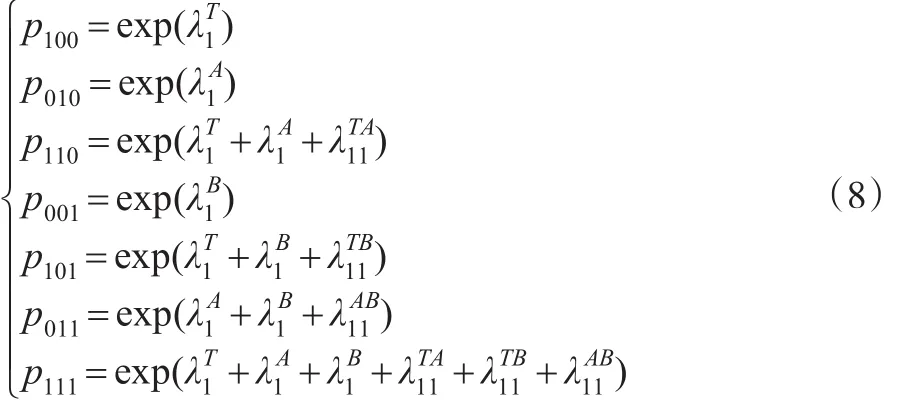
求解可得:

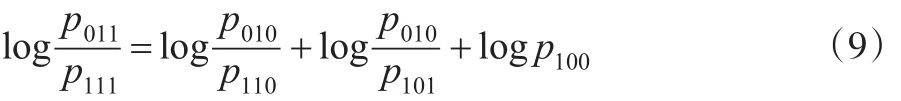
对式（9）进行logit变换，可得：

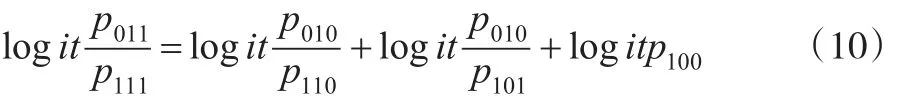
当 p100已知时，由式（9）可以推导出 θ11、θ10、θ01的关系表达式。p100实际是目标总体T内，数据库A和数据库B的不足涵盖误差，后文将p100记为pu。

当然，也可以对Log-linear模型进一步简化，但是这有可能导致一些不合理的假设。例如，额外假定，可以得到：

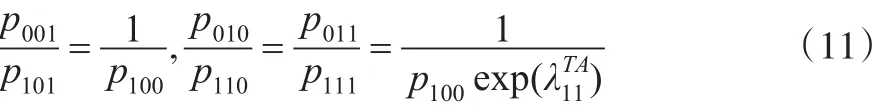
因此，由一般对数线性模型推导出的式（10）提供了θ11、θ10、θ01的一个关系表达式。将式（5）与式（10）联立，即可得式（12）：

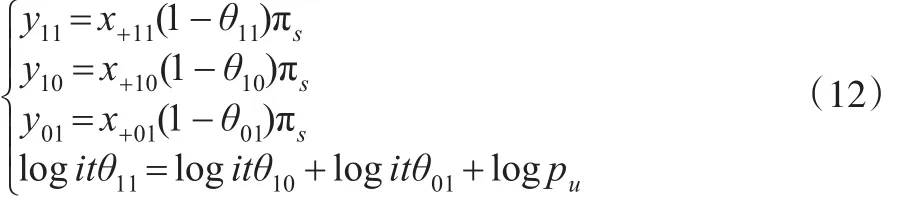
当 θab的值较小时，logitθab与 logθab的值相差很小，如 logit0.1=-2.2，log0.1=-2.3。因此，用 log替换式（12）中的logit，可得式（13）：

式（13）是式（12）的一个近似估计。式（12）和式（13）中除了待估参数 θ11、θ10、θ01与 πs外，还包含未知参数 pu。

因此，下文构建TL=A∪B，与抽样调查S产生的数据库匹配得到表6，采用双系统模型估计不足涵盖误差pu。

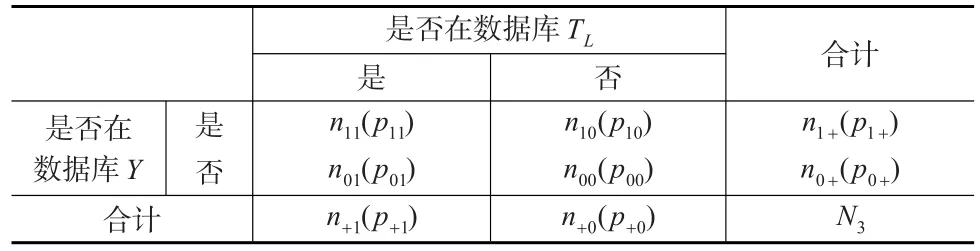
表6 TL与抽样调查S数据库匹配

根据抽样调查S的假设条件，显然，由抽样调查产生的数据库S与数据库TL满足捕获再捕获模型的四个经典假设[12]：

（1）数据库TL和数据库S针对的同一调查总体的总量不变，即总体封闭。

（2）任意调查个体在数据库TL和数据库S中分别被登记的概率不变。

（3）数据库TL和数据库S的来源途径相互独立。

（4）数据库TL和数据库S的调查个体记录信息能匹配。

根据双系统估计模型，可得到总体的总数估计：

因而，可得 pu的估计量：

令 x+10=x1，x+01=x2，x+11=x11，n+1=n1，n+1=n2，对式（12）和式（13）进行整理，可得质量评价模型1和质量评价模型2，分别如式（16）和（17）。

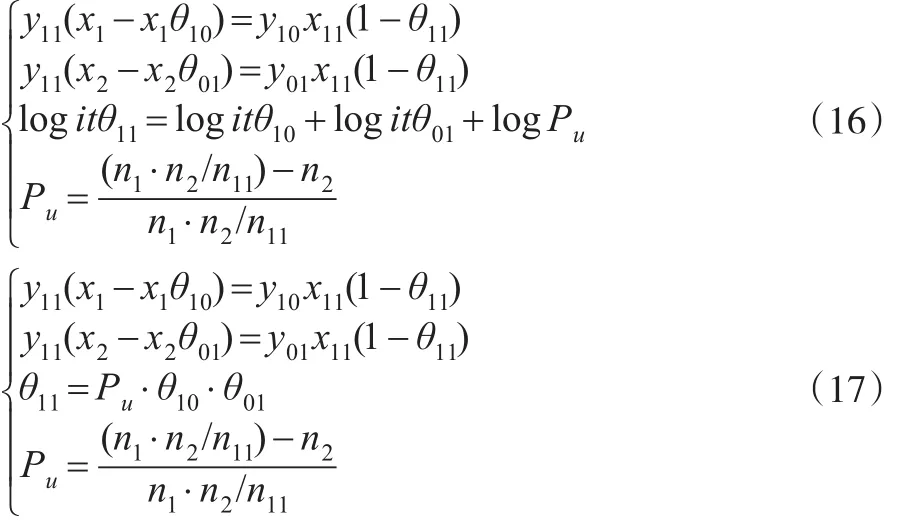
质量评价模型1和模型2是基于一般对数线性模型和双系统估计模型构造的，因此很容易扩展到多个数据库的情形。质量评价模型1包含logit函数，无法得到未知参数的显示解，实际中需要通过Mathematica等软件求解。模型2是模型1的一个近似估计，存在显示解，如式（18）所示。

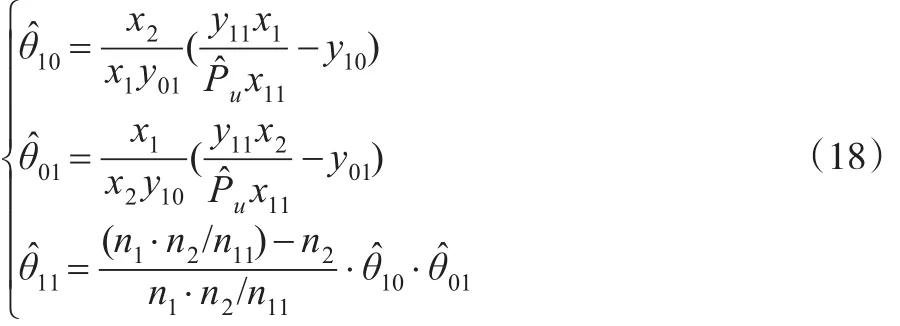
同时，在使用双系统模型估计不足涵盖误差pu时，没有剔除过涵盖误差的影响，因此可对pu的估计量进一步改进和完善。实践中可通过抽样调查估计过涵盖倾向性系数γ，对 pu的估计量进行调整，如式（19）所示。若过涵盖倾向性系数γ=0.01，则数据库TL中每个个体的实际作用为1/1.01=0.99。

2.4 模拟

为了比较质量评价模型的测量差异以及模型的拟合效果，采用数据表7和数据表8对质量评价模型拟合。表7中，数据库A包含900个样本，数据路B包含1100个样本，既在数据库A也在数据库B中的样本数为800，在数据库A但是不在数据库B中的样本数为100，在数据库B但不在数据库A中的样本数为300。数据库A和B的错误记录数分别为45和75，数据库A∩B中的错误记录数是e11，e11是变化的数值，且1≤e11≤45。当e11确定后，在数据库A但是不在数据库B中的错误记录是45-e11，在数据库B但是不在数据库A中的错误记录是75-e11。表7和表8的数据显示，表7中错误记录较少，表8中错误记录较多。两组模拟数据中均假定不足涵盖误差Pu=0.15，经过涵盖调整的Pu=0.10。

表7 模拟数据1

表8 模拟数据2

由质量评价模型中θ10、θ01、θ11的关系式可得到每个模型下 e11的取值，进而得到(θ10、θ01、θ11)的估计值。具体如表9所示。

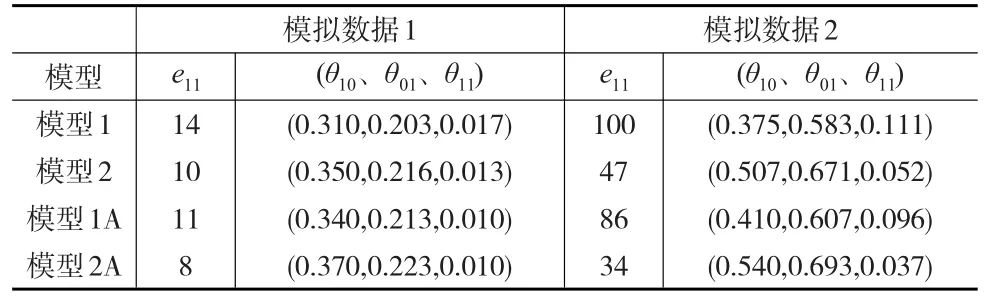
表9 模拟结果

表9的结果显示在模拟数据1下，模型1和模型1A的(θ10、θ01、θ11)估计值分别为(0.310,0.203,0.017)和(0.340,0.213,0.010)；模型2和模型2A的对应估计值分别为(0.350,0.216,0.013)和(0.370,0.223,0.010)。这表明经调整后的θ10、θ01和θ11估计值与未经过涵盖调整的估计值有差异。同样的现象也出现在模拟数据2中。但在两组模拟数据下,调整与未经调整的估计值差异并不明显。鉴于模拟实验中不足涵盖误差值与经过涵盖误差调整的不足涵盖误差值均是假定数据，在实践应用中有必要对不足涵盖误差做过涵盖调整。

在模拟数据1下，模型1A和模型2A中e11的取值分别为11和8。估计值分别为(0.340,0.213,0.010)、(0.370,0.223,0.010)，两者非常接近。这表明当错误记录较少时，可用模型2A直接估计数据融合中的过涵盖误差。在模拟数据2下，模型1A和模型2 A中e11的取值分别为86和34，据此计算而得的θ10、θ01、θ11估计值相差较大。这表明当错误记录数较多时，使用模型1A估计数据融合中的过涵盖误差更为精确。

3 讨论

以大规模、跨领域、多元异构、动态演化为主要特征的大数据源在政府统计、公共安全、商业数据挖掘等领域发挥了越来越重要的作用，相应的数据存储、融合、分析和理解也面临着重大挑战。当下亟待解决的问题是如何对数据关联、交叉和融合实现中的数据质量进行检测，以实现数据价值最大化。本文基于对数线性模型和双系统估计方法，建立可扩展到多个数据库融合情形的数据融合质量评价模型，通过模拟研究，比较四个模型的优劣，给出不同模型的适应条件。实际应用中，为测量数据库A和数据库B的融合质量，仅需根据工作目标做一个只包含不足涵盖误差的抽样调查，就可估计出融合后数据库 A∩B、A-A∩B、B-A∩B下的误差水平。尤其是当数据库中错误记录较少时，可采用模型2的显示解直接估计过涵盖误差。无疑，该方法能在政府、企业和社会全面数据资源开发中得到重要应用，为数据整合汇聚、建立大数据云和重点领域专题数据库提供质量保证。