收缩法和PR算法在加权复杂网络节点重要性评估中的比较

程 晨，李 贺

（1.贵州财经大学 马克思主义学院，贵阳 550004；2.国家行政学院 经济学部，北京 100089）

0 引言

复杂网络（Complex Network），是具有自组织、自相似特性的幂律的度分布概念，是现代商业发展的重要系统论基础。如商业伦理研究的就是商业与社会的复杂网络关系，其核心是商业活动中人与人的伦理关系。良性商业伦理关系能够促进经济循环增长，但近来年，一些因利益原因出现的贿赂、背叛、悔约等现象，严重破坏商业伦理的理想秩序，给经济和社会带来一系列的负面影响[1]，因此，商业伦理的抗毁坏性研究在市场经济领域成为焦点。但以何种方法进行定量研究则争执不一，魏赟鹏[2]将商誉价值设定为商业伦理指标变量，利用成本计量方法试图论证商业伦理在商业决策中的作用。该方法能够为商业伦理在商业决策中提供参考指标，但存在两点缺陷，一是无法提前估算商誉未来价值，二是无法对商誉成本做出正确的计量估算。肖岳峰[3]从核算模型角度进行商业伦理数理核算，计算出商业伦理作用系数和强度系数。该方法结构明确，而且结果以定量数值方式表示，较为合理。但计算过程中存在层次结构模型，专家评分主观因素较多，对模型定量数值存在一定影响。

目前学术缺陷和研究不足，造成商业伦理重要性程度评定研究并不完善。实际上商业伦理是一种人际关系模式，符合复杂网络定义中自组织、自相似、吸引子、小世界、无标度等特征，是典型的复杂网络小世界。因此将商业伦理纳入复杂网络研究范畴，构建商业伦理复杂网络。复杂网络研究中节点重要性评估方法相对成熟，对商业伦理复杂网络节点重要性评估具有重要借鉴意义。本文以收缩法和PageRank算法为研究工具，对评估过程和计算结果进行对比，以确定最佳研究方法。

1 加权商业伦理复杂网络

商业伦理网络作为人际关系的特例，是一种具备动力学行为和复杂拓扑结构的规模性网络，符合复杂网络的基本定性。但传统的无权复杂网络研究方法主要持统计学及物理学方法，仅定性商业伦理网络中人际关系的几何性质和形成结构，只认定商业伦理复杂网络中的节点是否存在相互作用，忽略商业伦理复杂网络并不是一个简单的布尔网络，各节点之间的相互作用因多种因素存在强度差异[4]，如商业伦理中亲情关系、利益因素等。因此在无权复杂网络基础上引入加权复杂网络，形成加权后的商业伦理复杂网络。实际上引入复杂网络并不简单，需对商业伦理复杂网络中的边权进行赋值，以反应商业伦理复杂网络中各节点间的作用强度。一般边权赋值采用物理权重和抽象权重两种指标作用参考指标，取二者综合值作为最终边权值[5]。而在处理权重关系时一般采用相异或相似原则，相异原则一般表示商业伦理复杂网络中的空间分布，如商业伦理中二个个体居住距离，相居较远则权值越大，二节点关系越疏远。相似原则相反，一般表示商业伦理复杂网络中主观因素，如商业伦理中二个个体为战友关系，则权值越大，二节点的关系越亲密[6]。

下面给加权商业伦理复杂网络进行基本的定量统计描述。假设商业伦理复杂网络的集合为G=(V，E)，那么商业伦理复杂网络中个体即为节点，个体之间联络方式或人际关系度为商业伦理复杂网络权重，即边权。定义商业伦理复杂网络中的节点集合为 υ={υ1,υ2,υ3,…υn}，υi(i=1，2，3…)为网络中的一个节点,边权集合为e={e1,e2,e3,…en} ，用邻近矩阵M表示。则有加权商业伦理复杂网络的节点数n=|υ|，连接边数m=|e|。一般情况下节点集合υ={υ1,υ2,υ3,…υn} 比较易得到，但加权商业伦理复杂网络中边权集合e={e1,e2,e3,…en}由于边权差异不适用三角形不等式，边权的节点强度ψ需经特殊处理才可得到。同时考虑加权商业伦理复杂网络中边的连接方式存在无向和有向二种，节点强度ψ的计算方式分二种。

第一，无向连接网络节点强度ψ计算。加权商业伦理复杂网络无向连接中，邻近矩阵M为对称矩阵，那么边权ω 中ωij=ωji(i，j=1，2，3…) 。如果节点之间由边 ωig和ωgj相连，那么，当两节点相异时，则节点之间的距离Lij=ωig+ωgj，当两节点相似时，则节点之间的距离。最终节点之间的平均距离为：L=，在此基础上，得到无向连接下加权商业伦理复杂网络中节点强度

第二，有向连接网络节点强度ψ计算。加权商业伦理复杂网络有向连接中，节点强度分为入强度ψin和出强度ψοut。假设二节点υi，υj由二条有向边相接，二条边的边权值分别为，那么入强度为指向节点υi的集合，出强度为节点 υi的指向集合）。

理论显示，在加权商业伦理复杂网络中的节点强度存在显著差异，节点强度具有网络抗毁性，如果5%的核心节点被侵占，则某个加权后的商业伦理复杂网络有可能进入无序状态，甚至使整个商业伦理网络陷入混乱[7]，因此对加权后的商业伦理复杂网络进行节点重要性评估成为重点。依据传统理论，分析节点强度ψ可排序加权商业伦理复杂网络的节点重要性，但该方法排序过程中忽视桥节点，排序结果较为片面。而以节点间的最短路径几率作为排序标准，则由于模型的复杂程度较高，排序结果容易出现计算错误。

2 收缩法的加权商业伦理复杂网络节点重要性评估

收缩法的核心思想是将加权商业伦理复杂网络中节点υi与邻近相连的节点结合，形成新的节点，之前与节点υi相连的边重新与节点相连。收缩后的节点与加权商业伦理复杂网络凝聚在一起，一般用网络凝聚程度∂(g)表示新节点的重要度，数值为节点数n与平均路径长度L的乘积倒数[8]。即：

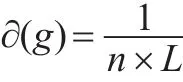
进一步优化后：

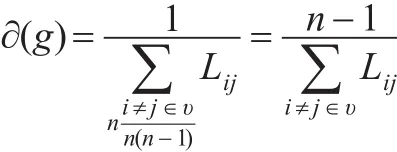
其中Lij表示二节点最短距离，n≥2。那么收缩后加权商业伦理复杂网络中的节点重要度为：

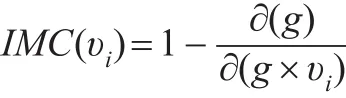
综上述，收缩法对加权商业伦理复杂网络节点重要性评估综合了节点数目及节点连接边权，如果节点υi的邻接节点数目越少，位置越重要，则收缩后的节点网络凝聚程度越高，显然有悖常理。

2.1 优化网络凝聚程度∂(G)

前述收缩法借鉴无权复杂网络构建加权商业伦理复杂网络的网络凝聚程度，忽略了加权商业伦理复杂网络存在边权差异，节点数n与平均路径长度L的乘积倒数并不能完全表示收缩后加权商业伦理复杂网络的凝聚度。因此前述网络凝聚程度∂(g)值并不能直接使用，需要从加权商业伦理复杂网络维度进行优化，并将时间复杂度纳入考察范围。假设存在加权商业伦理复杂网络G=(V，E)，该网络各节点之间相互独立，连接边数少于或等于1，边权相异且ω∈(1,+∞)。那么对该网络进行优化收缩，首先将节点υi与邻近节点关联形成新节点υi'，边权为收缩圈边缘的边权值，如图1所示：

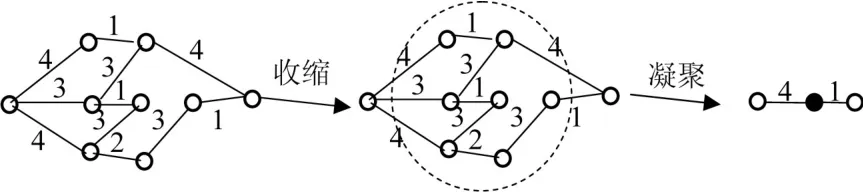
图1 节点收缩示意图

然后计算收缩后的网络凝聚度∂(G)，此时需要考虑边权差异，用平均点权之和s与退化为无权商业伦理复杂网络后的网络平均距离l乘积倒数表示，目的在于避免边权差异和路由变化对收缩后计算结果造成影响，即：

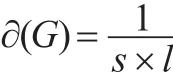
进一步优化后：

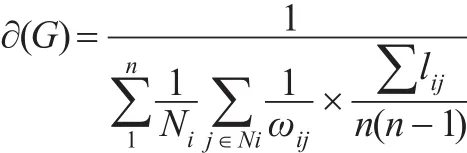
其中lij表示二节点加权路由路径下的无权最短距离，n≥2。那么优化收缩后加权商业伦理复杂网络中的节点重要度为：

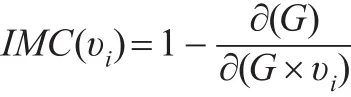
从优化后的收缩加权商业伦理复杂网络节点重要度公式来看，节点重要度主要取决于节点网络位置和节点连接数。如果节点处于网络关键位置，最短路径越少，收缩后平均距离lij变化越大，那么网络凝聚度∂(G)值越大。如果节点连接数目越多联系越紧密,收缩后节点的点权均值和数目越少,那么网络凝聚度∂(G)值越大。

2.2 节点重要性程度评估算法改进

收缩法与节点间最短路径评估方法类似，即采用节点间最短距离的线性关系进行复杂度优化计算。但由于加权商业伦理复杂网络需采用Floyd循环算法，导致整个计算过程时间复杂度超过无权复杂网络，由O(n3)变成了O(n4)，故需对加权商业伦理复杂网络节点重要性程度评估计算过程进行改进。根据前述网络凝聚程度思路，除计算加权商业伦理复杂网络中的平均点权之和s和退化为无权商业伦理复杂网络后的网络平均距离l外，继续引入节点连边的重要度计算。假设加权商业伦理复杂网络G=(V，E)的边为节点，而网络中的各边由边连接，那么即可将网络G=(V，E)收缩为G=(V，E)'，利用优化后网络凝聚程度的计算方法重新评估网络G=(V，E)'节点重要度，叠加网络G=(V，E)与网络G=(V，E)'的节点重要度。其计算公式如下：

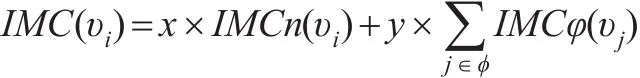
式中 φ 为节点集合，IMC(υi)和 IMCφ(υj)分别表示网络G=(V，E)和G=(V，E)'中对应节点υi的节点重要度和连边节点重要度，考虑网络为加权网络，用x、y分别表示节点重要度和连边重要度的加权系数。为便于理解，使用改进算法后的节点连边示意图进行说明，见图2。

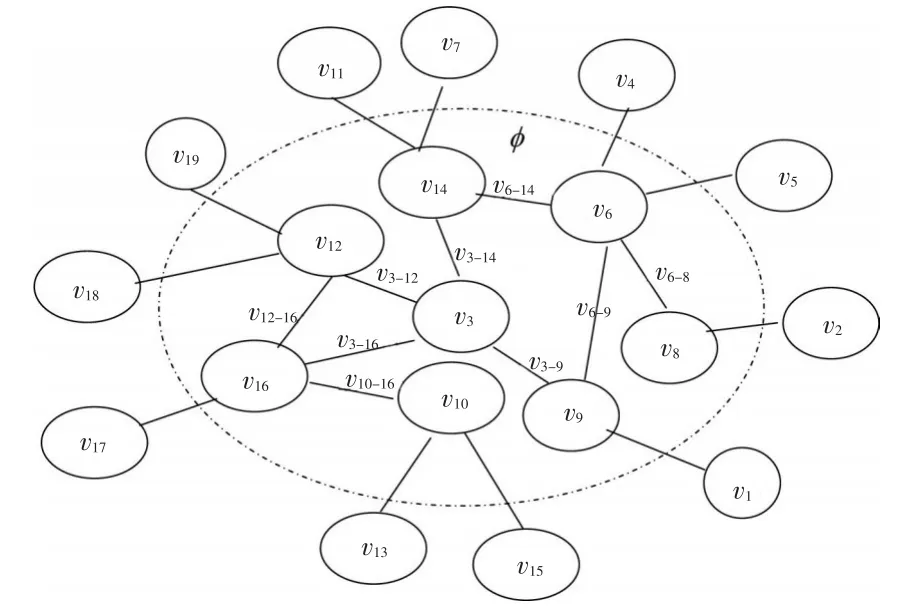
图2 改进算法后的节点连边图

从计算公式和示意图可见，改进算法后的收缩法，节点重要性评估取决于节点数目、节点位置、节点连边重要度及节点重要度和连边重要度的加权系数x、y，相对而言，该收缩法属于较为全面的研究方式。但同时存在计算结果大于1（即IMC(υi)＞1）的情况，因此需要对节点重要度 IMC(υi)的计算结果进行归一化处理，用 IMCf(υi)表示，归一化处理结果如下：

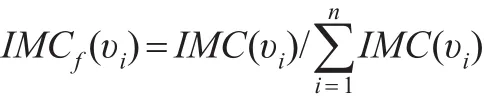
总结改进收缩法的计算过程发现，收缩法计算商业伦理复杂网络节点重要度的核心思想还是网络凝聚程度，只是收缩法在网络凝聚程度基础上，将变量因素从节点数和平均路径长度扩展到平均点权之和、网络平均距离和节点连边的重要度。尽管收缩法中间计算过程将时间复杂度由O(n)3变成O(n)4，但通过改进收缩法后时间复杂度为O(n)3，整个算法的复杂度为O(n)3，对于加权商业伦理复杂网络节点重要度的计算较为理想。

3 PageRank算法的加权商业伦理复杂网络节点重要性评估

3.1 PageRank算法

PageRank算法由Google搜索发展而来，最初是为解释Google搜索引擎中网页排名问题，依据某网页如被更多网页链接，则认定某网页的排名度更高[9]。因此PageRank算法实际是体现网页之间的相对链接关系，如图1中①→②表示网页①中有链接链向网页②，则说明①为网页②贡献了PageRank值。图3共示意了7个网页的链接关系。

可以看出PageRank算法中的网页权重关系，由链向某网页的链接数量投票决定，网页被链向则意味权重值增加，网页最终权重值为链向该网页的权重值之和，用公式表示如下：

式中 PR(α)为网页 α 的PageRank值，PR(β)、PR(x)、PR(δ)…则表示网页 β 、x、δ…链向网页 α 的PageRank值，而C(β)、C(x)、C(δ)…分别表示网页 β 、x、δ…链向其他网页的数量,因此可得出网页α的PageRank值矩阵,其中αmn=PR(n)/c(n)。

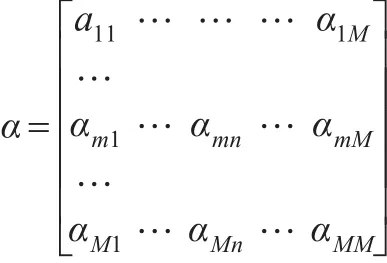
由网页α的PageRank值矩阵可知，如果某网页存在链向其他网页链接，则证明该网页对其他网页贡献了PageRank值，但该网页贡献的PageRank值大小取决于该网页的重要程度，网页越重要其贡献的PageRank值越大。上述结论的基础是网页链向是单向链接，由于实际网页链接存在双向链接，故网页的PageRank值计算属于一个迭代过程。假设向量 β(β1，β2，β3，…，βn)（其中 β0=(1，1，1…，1)）为网页的PageRank值排序，那么网页PageRank值的第i次迭代结果为：

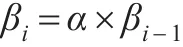
理论表明βi存在收敛现象，而且网页之间的链接关系属于概率事件，存在概率为0或1的可能，故对迭代结果进行平滑处理，引入平滑处理因子∂=0.85，单位矩阵用ℜ表示，网页数量用n表示，结果如下：

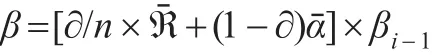
通过上述处理后，如果假设条件为网页的初始权重值为1，那么可得到图1网页链接关系的PageRank值矩阵。

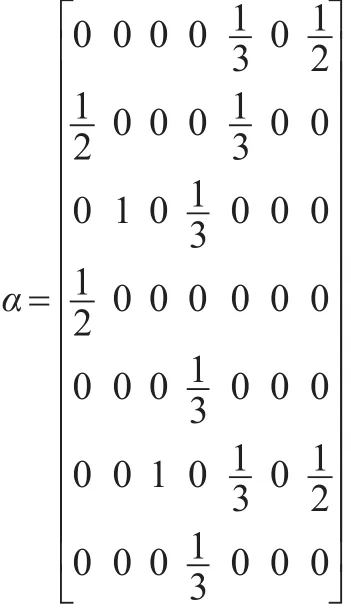
显然，PageRank排序算法能够准确的将网页重要程度进行排列，并且具有可靠性。对比网页的PageRank排序算法发现，实际上商业伦理网络各节点之间的联系就是一个类似网页链接关系，商业伦理网络节点之间是否关联，节点的重要性程度如何，亦可用类似节点之间是否存在“链接”表示。因此PageRank排序算法对商业伦理复杂网络节点重要程度的排序具有重要的借鉴意义，接下来借鉴PageRank排序算法对加权商业伦理复杂网络中的节点重要程度进行演算。

3.2 Page Rank算法与加权复杂网络的结合

既然引入PageRank算法，那么对商业伦理加权复杂网络的节点重要性重新定义评估指标WG-PageRank。但上述PageRank算法存在缺陷，PageRank算法考虑了网页链接中的迭代现象，却将网页中的初始权重值全部定义为1。商业伦理复杂网络中由于各节点中的关系影响（如亲人、同学等），导致各节点中的初始权重值并不相同，因此在商业伦理加权复杂网络中并不能将各节点初始权重值定义为1。故需对PageRank算法进行优化。假定在加权商业伦理复杂网络中有n个节点，其中节点υ与节点υ1、υ2、υ3、...υi相连，同时节点 υi对节点 υ的权重为 ω(υi,υ)，那么可定节点υ的重要性评估指标WG-PageRank如下：

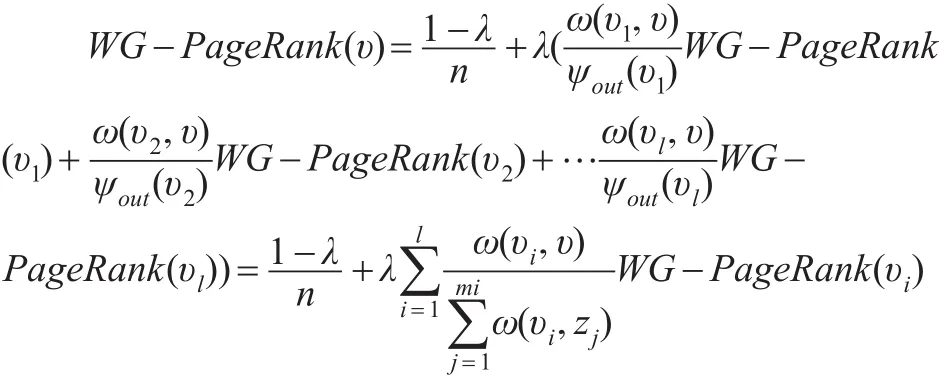
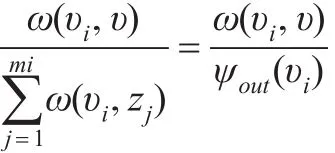
通过上述方法后，解决了网页PageRank算法中无法给不同节点赋值的缺陷，使之更加符合加权商业伦理复杂网络节点重要性评估运算的需要。

3.3 节点重要性程度评估

根据前述理论，商业伦理网络属于加权复杂网络范畴，定加权商业伦理复杂网络为G=(V，E),为对其重要性进行评估，首先找出邻接矩阵M，用矩阵M来表示网络G中n个节点的链接关系。

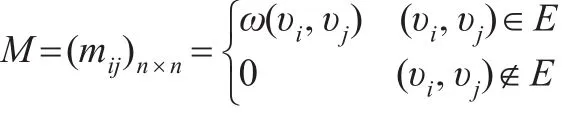
从邻接矩阵可以看出，加权商业伦理复杂网络中各节点的链接关系存在两种形式，即当两节点之间相链时，那么邻接矩阵M中的数值即为两节点的权重值，否则表示两节点之间不相链，矩阵M中的数值为0。考虑到一些封闭商业形式（如军事、保密行业等），商业伦理复杂网络中的节点并不向外链接，计算后邻接矩阵M中某行值全部为0，则称该节点为悬虚节点。另外，商业伦理复杂网络中的节点是否相链还是一个概率事件，因此还需要对邻接矩阵进行概率归一化处理，以记录矩阵M中各节点与另外节点接链的概率。处理公式如下：

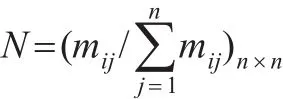
通过上述公式计算后，得到新矩阵N，即为概率转移矩阵。概率转移矩阵N中同样存在邻接矩阵M中的悬虚节点，为便于计算，用向量（1/n）eT置换概率转移矩阵N中全部为0的行，即可得到悬虚节点概率转移矩阵N'：

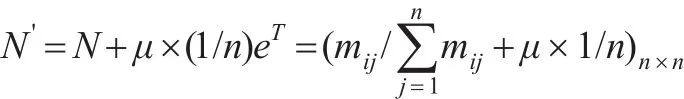
其中式中μ为一个二进制数字，用于判断某节点是否为悬虚节点，当节点为悬虚节点时，μ取值为1，否则为0。得到悬虚节点概率转移矩阵N'后，便可计算网络G的WG-PageRank值的矩阵α。由于每个节点与其他节点的链接一般存在阻尼，故引入阻尼系数λ，而且商业伦理复杂网络中主要分析链入关系，需要使用概率转移矩阵N'的转置矩阵N'T，得到结果如下：

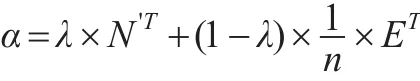
当矩阵中某行的数值全部为1时，ET=e×eT。计算后得到加权商业伦理复杂网络重要性矩阵α后，然后对节点重要性进行排序即可。总结PageRank算法在加权商业伦理复杂网络节点重要性评估中的运用后发现，该方法的时间复杂度为O(n2)，空间复杂度为O(n2)。

4 两种方法的实验对比

为验证改进收缩法和PageRank算法在加权商业伦理复杂网络节点重要性评估计算中的有效性，选择某沿海城市13家小型企业（相互之间存在关联）为研究对象，节点选择企业董事长，连接边以企业董事长2017年12月内是否通话为依据，连接边的权值即为2017年12月的通知次数，通过处理分析即可得到该加权商业伦理复杂网络的拓扑结构，如图4所示。

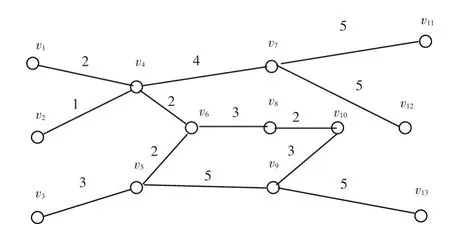
图4 某加权商业伦理复杂网络的树形拓扑结构

4.1 排序结果比较

利用本文提出的改进收缩法和PageRank算法估计该加权商业伦理复杂网络的节点重要度。考虑市场公平原则，定该网络中的节点为平等的合作关系，则收缩法中节点重要度和连边重要度的加权系数x=y=0.5。而PageRank算法中，阻尼系数λ数值大小能够体现节点相对重要度和决定算法迭代收敛速度，故将阻尼系数λ设置为合理的0.85，兼顾二者之间的平衡。设定加权系数和阻尼系数后，依据收缩法和PageRank算法，则可得到具体的评估结果和排序结果，见表1。

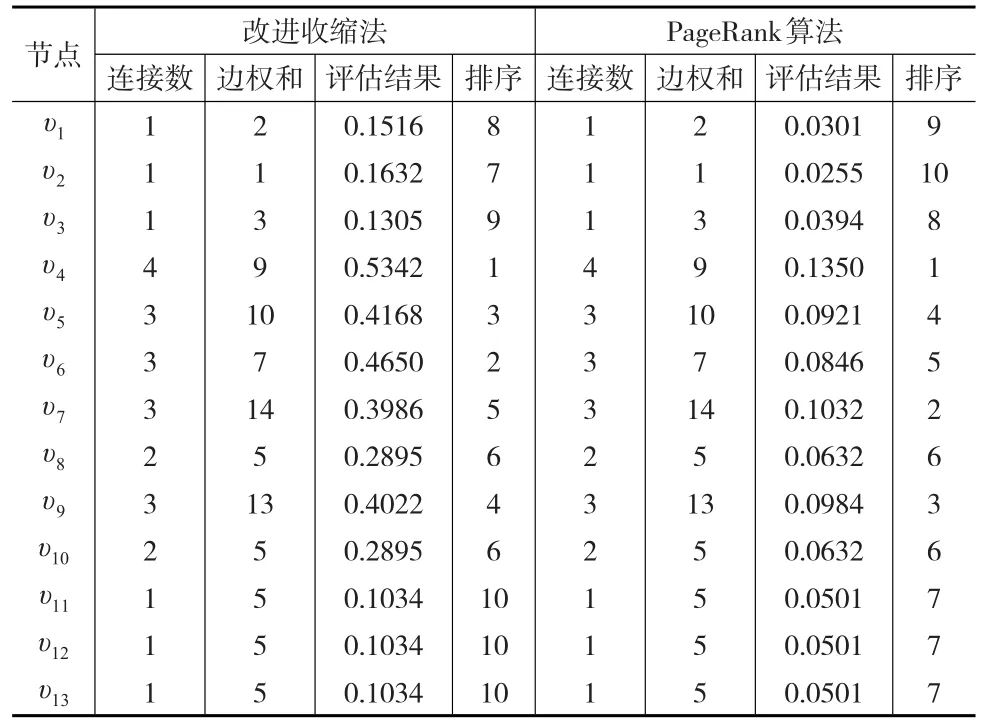
表1 改进收缩法和PageRank算法的节点重要度评估结果

从结果看，改进收缩法和PageRank算法的排序结果略有差异，改进收缩法排序结果为 υ4＞υ6＞υ5＞υ9＞υ7＞υ8=υ10＞υ2＞υ1＞υ3＞υ11=υ12=υ13，而 PageRank算法排序结果为 υ4＞υ7＞υ9＞υ5＞υ6＞υ8=υ10＞υ11=υ12=υ13＞υ3＞υ1＞υ2。其中节点υ4无论是改进收缩法还是PageRank算法，都处在该加权商业伦理复杂网络的关键位置，说明改进收缩法和PageRank算法对加权商业伦理复杂网络节点重要性评估的核心观点一致。区别在于PageRank算法相对改进收缩算法节点 υ7和 υ6、υ9和 υ5、（υ11、υ12、υ13）和 υ2、υ3和υ1的排序位置进行了更换，原因可能是由于PageR-ank算法考虑了节点连接边的方向性，对节点重要性的评估计算中考虑了入强度ψin和出强度ψοut。而改进收缩法偏向节点连接数目，节点重要度IMC(υi)的计算结果又进行过归一化处理，故其计算数值可能更接近节点重要度实际值，但排序结果可能与理论值有一定的偏差。由此可见改进收缩法和PageRank算法在加权商业伦理复杂网络节点重要性评估中各有千秋，但由于改进收缩法的排序结果更接近实际值，条件许可下，本文更偏向采用改进收缩法对加权商业伦理复杂网络的节点重要性进行评估。

4.2 运行时间比较

考虑时间成本，利用随机模型建立随机加权商业伦理复杂网络，分别采用改进收缩法和PageRank算法对随机网络中的节点进行重要性评估，通过多次运行得出运行时间的平均值，结果见图5。

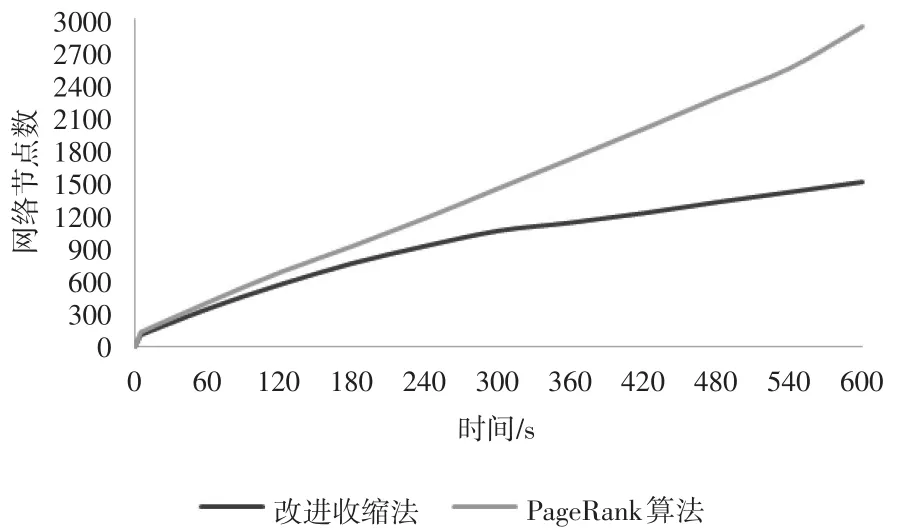
图5 不同算法和不同节点数目的运行时间

从图5可以看出，当加权商业伦理复杂网络中节点数目少于100时，改进收缩法和PageRank算法的运行时间基本控制在5s以内，而随着加权商业伦理复杂网络节点数目的增加，改进收缩法的运行时间明显长于PageRank算法，原因是由于改进收缩法需要消耗大量时间来计算平均点权之和、网络平均距离和节点连边的重要度等多个变量数值。由此可见，当评估小型加权商业伦理复杂网络节点重要性时，适合选取改进收缩法，而当评估大型加权商业伦理复杂网络节点重要性时，选取PageRank算法更能在时间上获得计算优势。

5 总结

将商业伦理纳入复杂网络研究范畴后发现，如果以传统无权复杂网络定义商业伦理复杂网络，则忽略了商业伦理复杂网络并不是一个简单的布尔网络，各节点之间的相互作用因多种因素原因存在强度差异。因此本文在无权复杂网络的基础上引入加权复杂网络，对商业伦理复杂网络中的边权进行赋值，以反应商业伦理复杂网络中各节点间的作用强度，从而构建加权商业伦理复杂网络。由于传统加权商业伦理复杂网络节点重点性评估方法不完善，本文引入收缩法和PageRank算法，并对二种方法进行实验对比。结果表明：

（1）改进收缩法计算商业伦理复杂网络节点重要度的核心思想是网络凝聚程度，只是改进收缩法在网络凝聚程度基础上，将变量因素从节点数和平均路径长度扩展到平均点权之和、网络平均距离和节点连边的重要度，改进收缩法时间复杂度为O(n3)，整个算法的复杂度为O(n3)。

（2）PageRank算法由网页PageRank算法演变而来，主要以节点之间的链向关系为依据，通过计算加权商业伦理复杂网络重要性矩阵对节点重要性进行排序，PageRank算法的时间复杂度为O(n2)，空间复杂度为O(n2)。

（3）从实验排序结果来看，改进收缩法的排序结果更接近实际值，PageRank算法接近理论值，在条件许可下，本文偏向采用改进收缩法对加权商业伦理复杂网络节点重要性进行评估，但对于大型加权商业伦理复杂网络节点重要性评估中，考虑时间成本条件下，则选择PageRank算法。