正态系数线性回归的区间估计模型

刘兆君

（山东工商学院 数学与信息科学学院，山东 烟台 264005）

0 引言

数据分析中的线性回归分析模型一般包括均值回归模型[1-3]与分位数回归模型[4-8]，这两个模型各有特色，在实际预测中都有广泛应用[2-8]。均值回归模型与分位数回归模型的一般形式都是采用线性主要部分加随机误差次要部分，其中均值回归模型对随机误差部分要求较高，为零均值同方差独立正态分布；而分位数回归模型对随机误差部分要求较低，是p分位数为零的独立同分布。在进行参数估计时，二者只追求线性主要部分与观测值的不同形式的逼近:一个是最小平方和最小，一个是加权绝对误差和最小，而不关心方差对参数估计的影响。事实上，方差对于线性主要部分与观测值的不同形式的逼近是有影响的，自然会影响参数估计的结果。在这一点上，均值回归模型是可以考虑方差对参数估计影响的，却没有做；而分位数回归模型则根本放弃方差对参数估计的影响。在上述两个模型中，自变量的系数都是常数。另外，上述两种模型对因变量取值的预测，都是点估计，没有给出估计的精确度与误差范围。对于均值回归模型，虽然学者们也做过有关的区间估计研究，但只是一元线性回归的内容有些结果，且形式复杂，计算麻烦，没有做到点估计与区间估计兼顾，难以满足实际需求。针对上述分析的均值回归模型与分位数回归模型的特点，可以考虑建立正态系数线性回归的区间估计模型，此模型以正态变量做自变量的系数，将均值与方差统一考虑，利用机会约束优化理论，构造因变量优化的点估计与区间估计，并利用计算机优化软件求解，得到因变量优化的点估计与区间估计结果。实证分析表明，此模型简单实用，能够较好地满足实际应用需求。

1 模型构建

设随机变量与一般变量之间的线性关系式为：

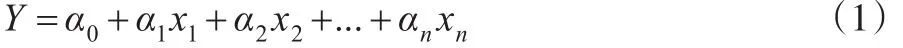
其中x1，x2，...，xn为可以精确测量或可以控制的一般变量，Y是可观测其值的随机变量，α0，α1，...，αn是相互独立的正态变量，假设αj～N(μj，σ2j)，j=0，1，2，...，n。则有：

显然：

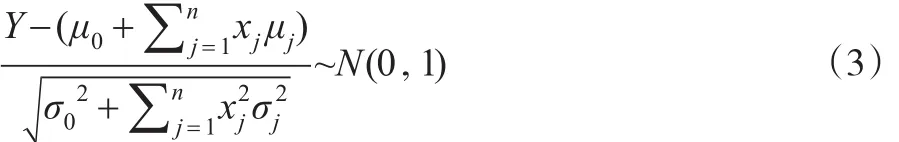
对给定的置信度1-α，0＜α＜1，查N(0，1)分布表，得分位数，其中Φ(x)表示标准正态分布函数，使得：

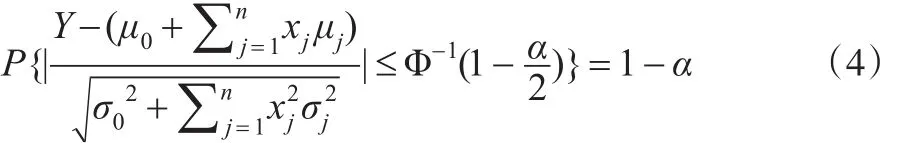
整理得：

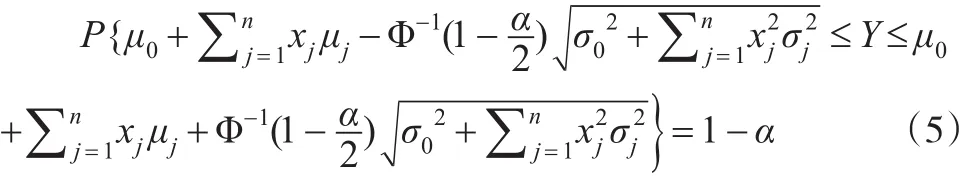
区间

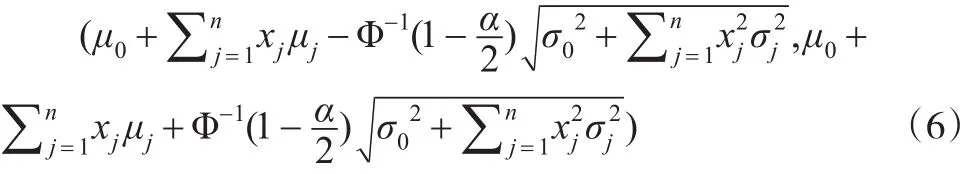
称为Y的置信度为1-α的置信区间。

为了获得一定置信度1-α下，0＜α＜1，随机变量Y的区间估计，本文做了m次独立观测试验，得到m组独立观测样本值：

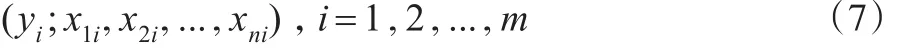
将式（7）代入式（1）可得：

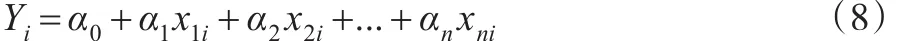
称为正态系数n元线性回归模型。

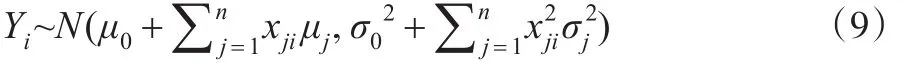
显然，式（8）与式（9）中Yi的观测值是yi，i=1，2，...，m。

在置信度1-α下，根据式（8）与式（9）做类似式（3）与式（4）的讨论，可得：

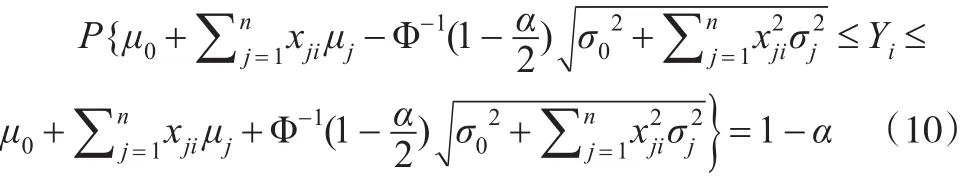
区间

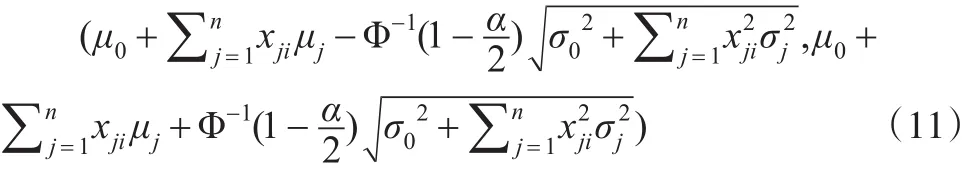
即为Yi的置信度为1-α的置信区间。

本文的目的就是要利用观测样本值式（7），估计未知参数μj，σj，j=0，1，2，...，n，得到估计值n，确定随机变量Y的置信度1-α的置信区间。

n元线性方程：

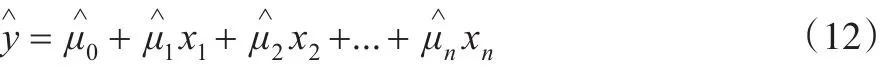
称为n元线性回归方程。对于式（7）中的每一组一般变量的取值 (x1i，x2i，...，xni)，由式（12）得：

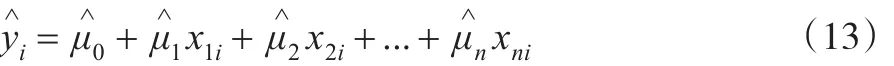
称为yi的回归值或拟合值。

一个好的置信区间式（6），应该满足下列两个原则:一是回归值的误差尽可能小；二是置信区间半径尽可能小。

未知参数μj，σj，j=0，1，2，...，n，的估计值0，1，...，n，就应该使置信区间式（6）满足上述区间估计的两个原则。

于是，构造下列随机规划：

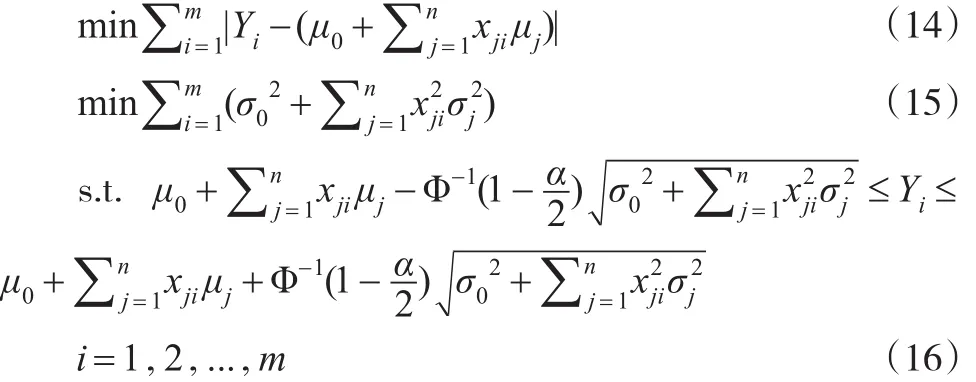
在给定置信度(1-α)m下，有下列机会约束规划：

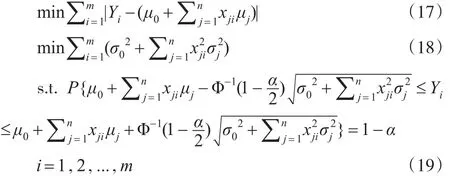
那么在给定置信度(1-α)m下，有下列等价的非线性规划：

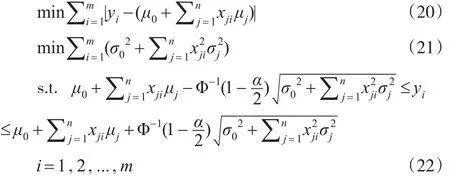
对于此多目标非线性规划，可以利用理想点方法转化为单目标的非线性规划，并应用LINGO 11优化软件，编程求解该单目标非线性规划，得到未知参数μj，σj，j=0，1，2，...，n，的估计值，从而确立随机变量Y的置信度为1-α的置信区间：

置信区间式（23）给出了回归值的带有置信度的误差区间，兼顾随机变量Y的点估计与区间估计。

2 实证

废气排放的预测与治理一直为人们所关注，能够较准确地预测未来废气排放的情况，对治理大气污染至关重要。本文以某省工业废气排放量及各影响因素的统计数据[9]（如下页表1所示）为依据，建立该省工业废气排放量与各影响因素的正态系数线性回归区间估计模型，实现对该省工业废气排放量的区间估计。

表1 某省工业废气排放量及影响因子数据

假设Y表示废气排放量，y表示其取值，x1表示工业总产值，x2表示能耗，x3表示治理设备数。

设置信度1-α=0.95，在此置信度下建立废气排放量Y的正态系数线性回归的区间估计模型。

由式（8）得：

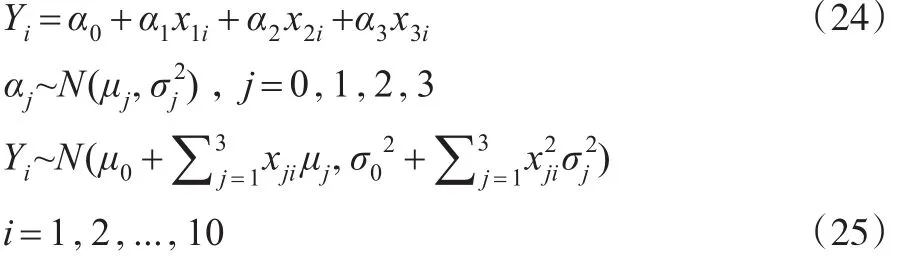
在置信度(1-α)10=0.9510下，可以确定下列机会约束规划：

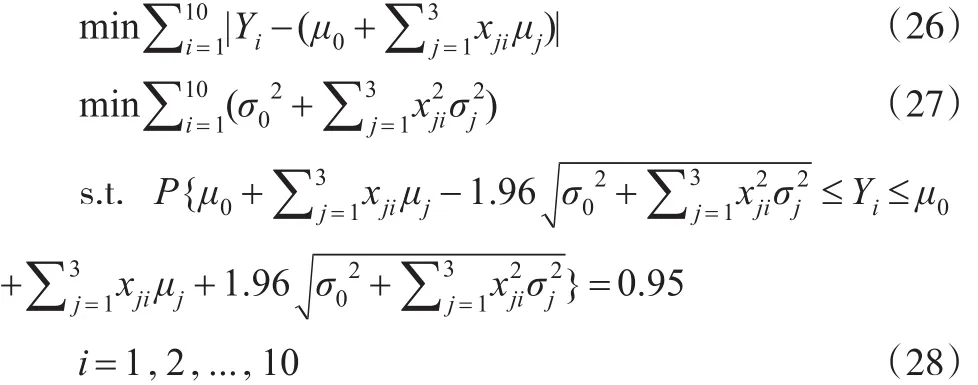
在置信度0.9510下，建立下列等价的非线性规划：

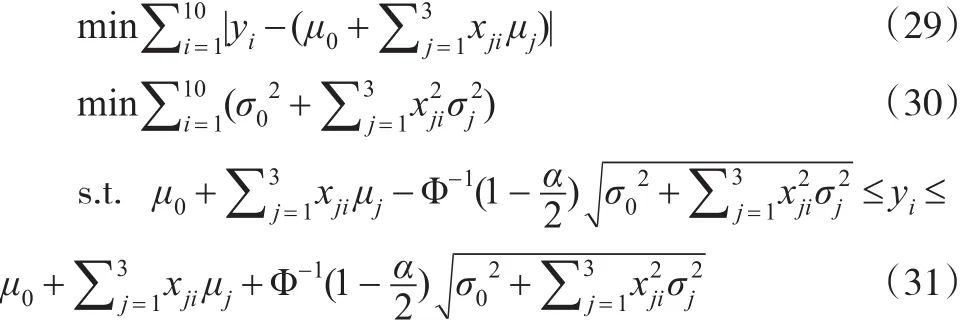
将表1中有关数据代入式（31），并利用LINGO 11编程求解，可得：

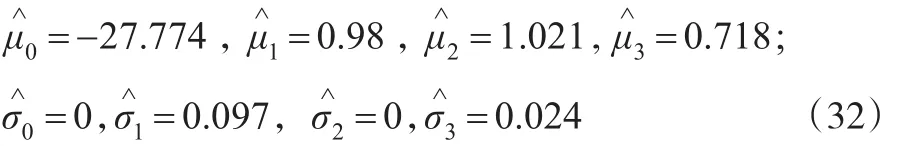
由此得到废气排放量Y与一般变量x1，x2，x3之间的线性关系式为：

且α0=-27.774 ，α1～N(0.98，0.0972)，α2=1.021,α3～N(0.718，0.0242)。

线性回归方程为：

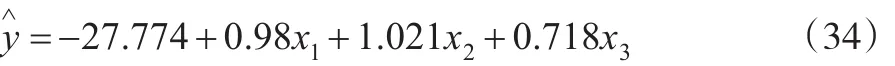
废气排放量Y的置信度为0.95的置信区间为：

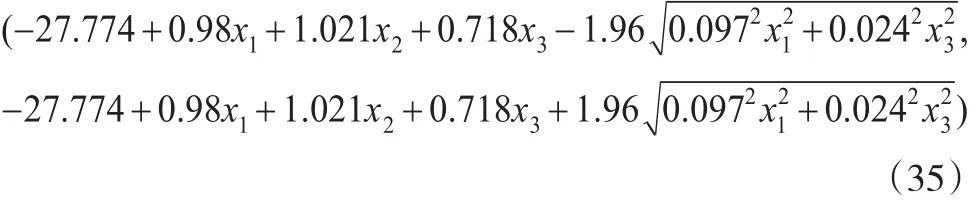
将回归值与置信度0.95的置信区间的计算结果列表，并计算回归值的平均相对误差（如表2所示）。

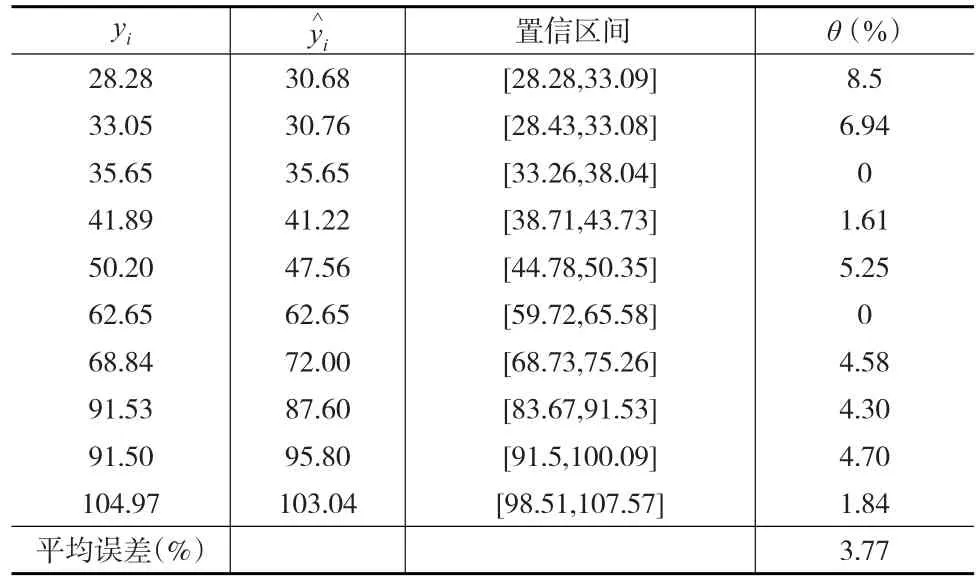
表2 置信度0.95正态系数线性回归区间估计效果

利用传统最小二乘法确定的线性回归方程[9]为：

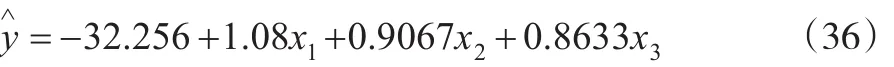
估计的σ值为=3.246，有关回归效果评价见表3所示。

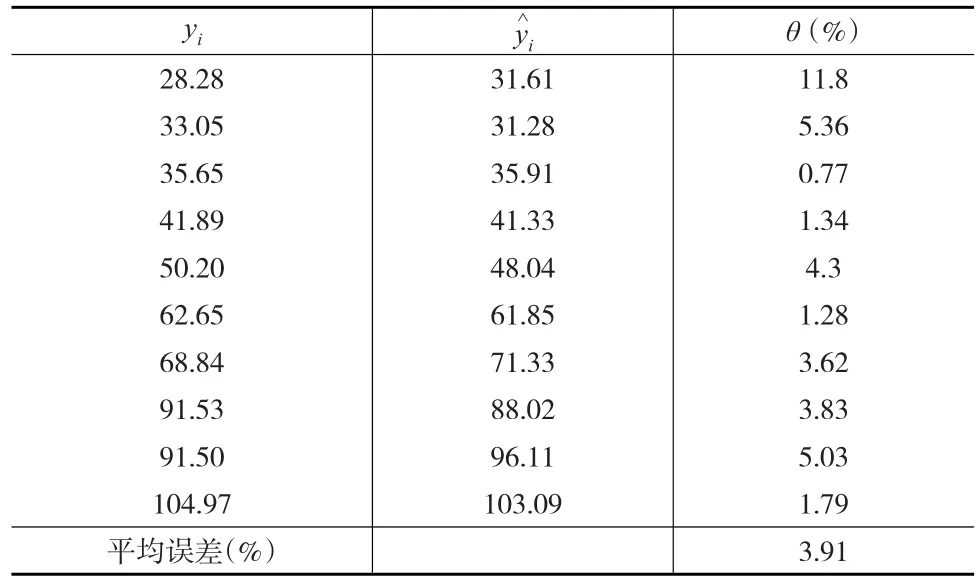
表3 传统线性回归效果评价

从表2与表3的对比中可以发现，正态系数线性回归区间估计模型的回归值的估计效果明显优于传统的最小二乘法，并且还给出了每一年废气排放量Y的可能取值的置信区间，实现了点估计与区间估计的统一。对比式（34）与式（36）可以看出，不同的预测方法所认定的各影响因素在废气排放量取值中的份量也是不同的：正态系数线性回归区间估计模型认定的各影响因素份量由高到低顺序为：能耗x2、工业总产值x1、治理设备数x3;传统的最小二乘法认定的各影响因素份量由高到低顺序为：工业总产值x1、能耗x2、治理设备数x3。很明显，正态系数线性回归区间估计模型有关份量顺序的认定更为合理，突出了主要因素“能耗”的作用，可以更有效地指导废气排放的治理工作。

3 正态系数线性回归区间估计模型的特点

正态系数线性回归区间估计模型，具有下列明显的特点:

其一，该模型充分利用了正态分布的信息，利用正态分布构造置信区间，还充分利用了正态分布的方差在估计未知参数中的作用。其二，该模型目标函数之一使用了最小一乘估计表达式，因此保持了最小一乘估计的一些优点，如模型的“稳健性”、预测的相对误差小等。其三，模型将点估计与区间估计有机统一起来，既能给出因变量的点估计值，又能给出因变量取值的区间估计，增强了模型的实用性。其四，模型的系数为正态变量，它可以表示自变量在因变量随机变化中所起到的作用。譬如在实证分析案例中，共有三个一般变量：x1表示工业总产值，x2表示能耗，x3表示治理设备数。在所得到的废气排放量Y与三个一般变量的线性关系式（33）中,x2的系数是常数，这表明能耗只能引起废气排放量Y确定性变化：不会引起废气排放量Y随机波动;而x1，x3的系数都分别为正态变量α1，α3，表明废气排放量Y是确定数量项与两个正态变量的线性组合，而x1，x3则是废气排放量Y随机性变化的确定性反映，能引起废气排放量Y的随机变化。其五，模型允许异方差的存在，并且能求出每一组一般变量所对应的正态分布的方差。最后要指出的是模型适合于因变量为正态分布的情况，本模型所使用的讨论方法具有一般性，同样适合于传统的均值回归模型。

4 结束语

对于线性随机系统可能状态的预测，已往的模型基本是倾向于点估计。利用多目标优化的思想，借助计算软件，兼顾点估计与区间估计，全面优化地解决线性随机系统预测问题，是此模型的特点，使得人们不仅能够获得复杂线性随机系统因变量取值的明确数量状态，还能统计推断复杂线性随机系统因变量取值的置信范围，让预测更加方便实用，可以较全面地满足实际应用中的各种需要。