周期函数及其性质的探究

龚凯宏

(江苏省启东中学 226200)

一、周期函数的定义

一般地，对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内每一个值时，都有f(x+T)=f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.

根据该定义可得到以下两个性质：

(1)如果f(x)定义在R上，且满足f(x+a)=f(x+b)，那么f(x)是a-b(a-b≠0)为周期的周期函数

证明因为f(x+a)=f(x+b)，所以x用x-b代换得：f(x+a-b)=f(x)，故命题成立.

(2)如果f(x)定义在R上，且满足f(x+a)= -f(x+b)，那么f(x)是2a-b(a-b≠0)为周期的周期函数.

证明因为f(x+a)= -f(x+b)，所以x用x-b代换得：f(x+a-b)= -f(x)，x再用x+a-b代换得：f(x+2a-2b)= -f(x+a-b)，因此有f(x+2a-2b)=f(x)，故命题成立.

二、几个定理

定理1 设函数y=f(x)定义在R上，其图象关于直线x=a与x=b对称(a≠b)，则f(x)是以2a-b为周期的周期函数.

证明因为f(x)的图象关于x=a与x=b对称，所以f(x)=f(2a-x)，f(x)=f(2b-x)则f(2a-x)=f(2b-x).根据性质(1)x用2b-x代换即得：f(2a-2b+x)=f(x)，因此f(x)是以2a-b为周期的周期函数.(当b=0时，它是偶函数)

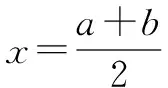
定理2 设函数f(x)是以2a-b为周期的周期函数，且f(x)的图象关于x=a(或x=b)对称，那么f(x)的图象关于x=b(或x=a)对称.

证明不妨设b>a,则2a-b=2(b-a)，因为f(x)的图象关于x=a对称，所以f(x)=f(2a-x)则f(x)=f(2a-x+2b-2a)=f(2b-x)，即f(x)的图象关于x=b对称.

定理3 如果函数y=f(x)定义在R上，其图象关于直线x=a对称，又关于点(b，0)对称，则函数f(x)是4a-b为周期的周期函数(a≠b).

证明因为f(x)的图象关于x=a对称，所以有f(x)=f(2a-x).又因为关于点(b，0)对称，有f(2b-x)=-f(x)，则f(2a-x)= -f(2b-x).此时x用2b-x代换得：f(2a-2b+x)= -f(x).根据性质(2)，x再用2a-2b+x代换得：f(4a-4b+x)=f(x)，因此，函数f(x)是4a-b为周期的周期函数.

推广如果函数y=f(x)定义在R上，其图象关于直线x=a对称，又关于点(b，c)对称，则函数f(x)是4a-b为周期的周期函数(a≠b).

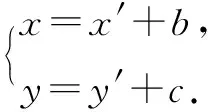
定理4 如果函数f(x)定义在R上，其图象关于点(a，0)与点(b，0)对称(a≠b)，则f(x)是以2a-b为周期的周期函数.

证明因为图象关于点(a，0)与(b，0)对称，所以f(2a-x)= -f(x)，f(2b-x)= -f(x)，则f(2a-x)=f(2b-x).根据性质1，x用2b-x代换得：f(2a-2b+x)=f(x)，因此函数f(x)是以2a-b为周期的周期函数.

在这里我们可仿定理2可证得：如果函数f(x)是以2a-b为周期的周期函数.且f(x)的图象关于点(a，0)(或(b，0))对称，则函数f(x)的图象关于点(b，0)(或(a，0))对称.证明略.

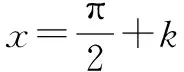
三、应用举例

例1 已知f(x+1)= -f(x)且f(1)=-1，则f(5)=____.

解因为f(x+1)= -f(x)，所以是以2为周期的周期函数，则f(5)=f(1)=-1.

例2 已知函数f(x)满足f(x+2)=f(x-2)，且f(x+4)=f(4-x)，当 -6≤x≤ -2时f(x)=x2+bx+c且f(-4)=-13，若m=f(b/3)，n=f(c/2)，p=f(11)，则m、n、p的大小关系为( ).

A．p

解由f(x+2)=f(x-2)得f(x)是以4为周期的周期函数.又因为f(x+4)=f(4-x),则f(x)又关于直线x=4对称,因此b=8,c=-61.而f(x)是偶函数,且在[0,2]上是增函数,则m=f(b/3)=f(8/3)=f(4/3),n=f(c/2)=f(-61/2)=f(3/2),p=f(11)=f(1),故p

例3 若函数f(x)的最小正周期是2004，而f(1002+x)=f(1002-x)对一切实数x都成立，则f(x)( ).

A.是奇函数而不是偶函数

B.是偶函数而不是奇函数

C.既是奇函数又是偶函数

D.既不是奇函数又不是偶函数

解因为f(1002+x)=f(1002-x)，所以x用x+1002代换得：f(2004+x)=f(-x).而f(x)以2004为周期，故f(x)是偶函数，选B.

例4 已知函数f(x)的定义域为R，对任意的x、y有 ①f(x+y)+f(x-y)=2f(x)f(y)，且f(0)≠0 ②f(π/2)=0.

(1)判断f(x)的奇偶性;

(2)判断f(x)是否为周期函数.

解(1)令x=y=0，得2f(0)=2f(0)f(0).∵f(0)≠0，∴f(0)=1.再令x=0得f(y)+f(-y)=2f(0)f(y)，∴f(-y)=f(y)，即f(x)是偶函数.

(2)令x=t+π/2，y=π/2得：f(π+t)+f(t)=2f(t+π/2)f(π/2)，即得：f(π+t)= -f(t)，则f(x)是2π为周期的周期函数.

例5 函数f(x)在R上有定义且满足

(1)f(x)是偶函数且f(0)=32;

(2)g(x)=f(x-1)是奇函数，试求f(2004)的值.

解由g(x)=f(x-1)是奇函数得f(x-1)的图象关于原点(0，0)对称，则f(x)的图象关于点(-1，0)对称.(把函数f(x)的图象向右平移一个单位即得函数f(x-1)的图象)而函数f(x)又是偶函数，所以得函数f(x)是以4为周期的周期函数.因此f(2004)=f(501×4+0)=f(0)=32.