高中数学解题中应用数形结合思想之探索

李沁芮

(重庆市南开中学 400030)

一、认识数形结合思想

对于高中数学来说，“数”和“形”是其中非常关键的构成部分，数量关系主要是以图象进行直观体现，而集合图形内也涉及到数量关系.所以，将“数”“形”进行融合来解答数学问题，这是非常高效的一种解题思想.通过对数形结合思想的实际运用，了解到其中包括两点内容：(1)以形助数；(2)以数解形.正确运用这两种方法，可以快速、正确地完成解题.

二、数形转化的有效方法

针对数形转化模式进行分析，其中包括三种转化模式：(1)形转数；(2)数转形；(3)数形互转.其一，形转数.这种模式一般是按照题目中的已知图形，经过详细审题之后便可以创造图象中隐藏的数量相关性，将几何图形所有属性以数这种形式进行体现.其二，数转形这种转化模式，一般是按照问题中的已知假设，画出相应的图形，图形可以表示既有数量关系，从而更加直接地了解数、形本质.其三，数形互转.这种模式主要是通过数、形之间的相互对立统一，详细观察图形之后，展开数、公式结构的分析，并展开联想，从而实现转化，将数学习题原本抽象、空洞的内容便成更为形象且直观的知识，帮助快速解题.

三、高中数学解题中应用数形结合思想

1.求解方程式习题

高中数学当中涉及到一元二次方程，面对这一类习题的求解，有时我们会遇到一元二次方程根分布的相关问题，这时可以使用二次函数图象进行求解.

例1 设f(x)=x2-2ax+2，当x∈[-1,+∞)时，f(x)>a恒成立，求a的取值范围.

解析：运用数形结合思想，可知这道题有两种解法.

第一种解法：由f(x)>a，在[-1，+∞)上恒成立⟺x2-2ax+2-a>0在[-1，+∞)上恒成立.函数g(x)=x2-2ax+2-a的图象在区间[-1，+∞)上位于x轴上方，如下图可知两种情况：

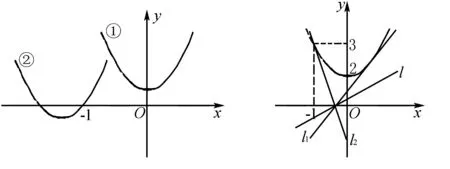
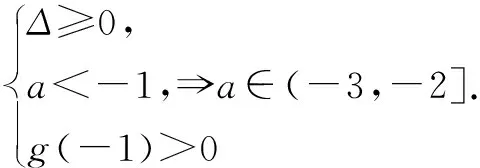
综上所述a∈(-3，1).

第二种解法：由f(x)>a⟺x2+2>a(2x+1)，令y1=x2+2,y2=a(2x+1),在同一坐标系中作出两个函数的图象,如图满足条件的直线l位于l1与l2之间，而直线l1、l2对应的a值分别为1，-3，所以直线l对应的a∈(-3,1).

2.求解函数解习题

函数有各自的表达式以及图象，解题时可以通过绘制图形的方式高效完成，展开数学计算也可以求解一些难度较高的问题.

例2 一家运输公司的运输设备分别包括7辆载重量6t的A型卡车、4辆载重量10t的B型卡车，驾驶人员为9名.某次该公司承包了每天搬运360t沥青的工作.已知每辆卡车每日往返次数如下：A型卡车8次，B型卡车6次.每辆卡车每日往返成本费如下：A型车160元，B型车252元.那么每日派出A型车、B型车多少辆，可以将公司成本控制到最低？

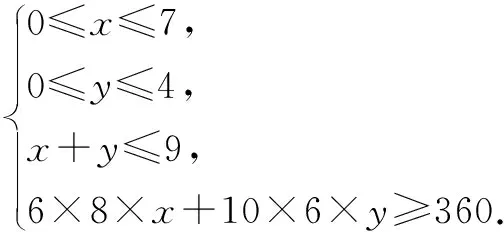
画出可行域图，保证z=160x+252y取最小值.

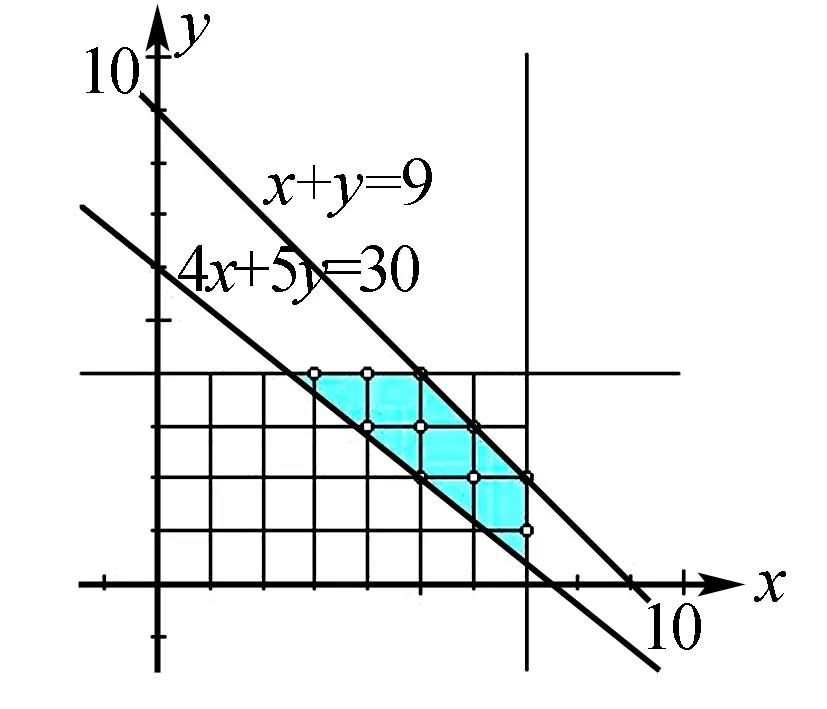
在可行域内针对某确定整数y，x取最小整数，也可以先定x，再定y的值，如此可行域内可能成为最优解的可行解如下：(7,1)(5,2)(4,3)(3,4)，将其代入到目标函数中，点(5,2)可以使公式z=160x+252y取最小值，计算可得最小值是1304元.因此，每日派A型车7辆，B型车1辆，这时可以将公司成本控制到最低.

3.求解集合类习题

一般我们面对集合类问题使用韦恩图的几率比较大，所谓韦恩图，即使用圆代表集合，若两圆相交，则证明集合内有公共元素，若两圆相离，则证明集合不包括公共元素.如此可见，韦恩图是求解集合类习题的有效方法.

例3 假设a、b为两个实数，A={(x，y)|x=n，y=na+b,n∈Z}，B={(x，y)|x=m，y=3m2+15,m∈Z}，C={(x，y)|x2+y2≤144}，是否存在a和b使A∩B≠Ø和(a，b)∈C同时成立.

解析集合A、B均为不连续点集，已知条件中给出“存在a、b，使得A∩B≠Ø”这一条件，即代表“存在a、b使得na+b=3n2+15(n∈Z)有解，解为(A∩B时x=n=m).根据主参数a、b，便可明确问题在几何角度的意义，即动点(a，b)在直线l：nx+y=3n2+15上，且直线与圆x2+y2=144有公共点，但原点到直线l的距离不小于12.应用数形结合思想，这道题同样有两种解法：

第一种解法：由A∩B≠φ得na+b=3n2+15

第二种解法：这一道题也可以使用代数方法求解.

由A∩B≠Ø可得na+b=3n2+15,即b=3n2+15-an. ①

由(a,b)∈C可得，a2+b2≤144. ②

将①代入②中可得关于a的不等式：(1+n2)a2-2n(3n2+15)a+(3n2+15)2-144≤0. ③

判别式Δ=4n2(3n2+15)2-4(1+n2)[(3n2+15)2-144]=-36(n2-3)2.

∵n是整数,

∴n2-3≠0，Δ<0.

又∵1+n2>0，故③不存在实数解.

∴不存在a、b，使得A∩B≠Ø与(a,b)∈C同时成立.

综上所述，数形结合思想在高中数学解题中运用，可以提高解题效率，降低问题难度，这对于增强高中生数学学习水平、综合素质发展有重要作用.