例说圆锥曲线中的范围与最值问题
2018-11-29 07:10赵春雷
数理化解题研究 2018年31期
赵春雷
(江苏省扬州市新华中学 225002)
一、圆锥曲线的范围问题常见求法
求圆锥曲线中的范围问题,主要用到两种方法:一是几何法.几何法就是指如果题目中的条件和结论能明显体现几何特征和意义,则考虑利用图形性质来解决.二是代数法.代数法就是指如果题目中的条件和结论能体现一种明确的函数关系,或者不等关系,或者已知参数与新参数之间的等量关系等,则利用这些去求参数的范围.
例1 [2016·浙江卷] 如图所示,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.
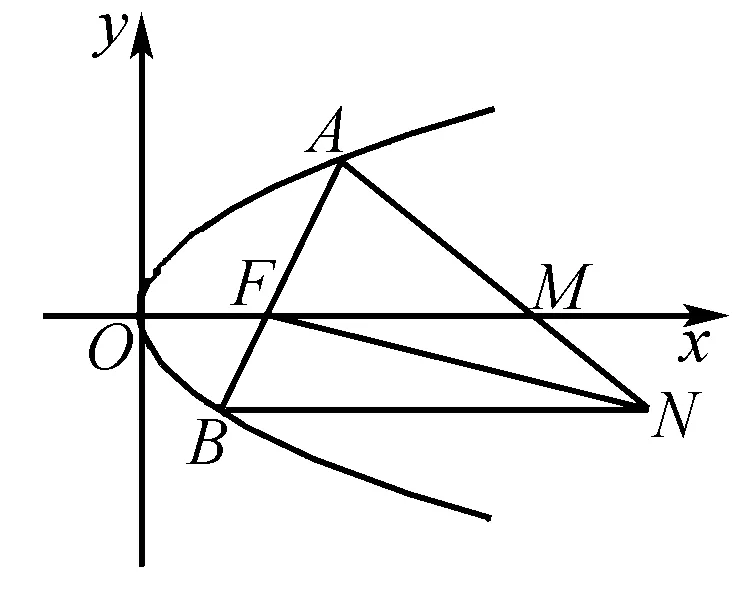
(1)求p的值;(2)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x轴交于点M,求M的横坐标的取值范围.
解(1)由题意可得,抛物

(2)由(1)得,抛物线方程为y2=4x,F(1,0),可设A(t2,2t),t≠0,t≠±1.因为AF不垂直于y轴,所以可设直线AF:x=sy+1(s≠0).
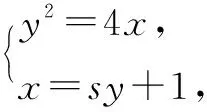
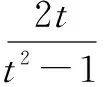
综上,点M的横坐标的取值范围是(-∞,0)∪(2,+∞).
评注本题的难度不算太大,在第一题中已经把抛物线的方程求出来了,到第二题时就可以直接应用了.第二题是求范围的典型题目,在分析了本题后,发现要想求解还是应该用代数法来求解,因为题目中给了一些数量关系,而这些数量关系正好能联立得到方程组.
二、圆锥曲线中面积的最值问题求解方法
一般来讲,圆锥曲线中面积的最值问题求解方法主要有三种.一是转化为面积与某参量的函数,利用函数的性质求最值;二是得到关于面积的关系式后,利用基本不等式求有关最值;三是结合圆锥曲线的几何性质求最值.
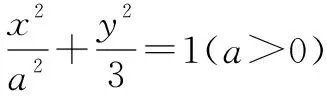
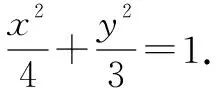
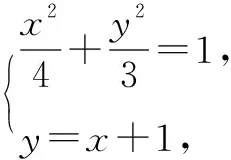
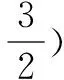
评注本题的难度较大,题目中的第一题和第二题相对简单,这道题是层层递进的,前两问是为第三题打基础的.在分析本题后,发现要想求解最后一题,先要得到关于面积的关系式,然后利用基本不等式求得最值.
猜你喜欢
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化·中考版(2021年10期)2021-11-22
河北理科教学研究(2021年4期)2021-04-19
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
数学年刊A辑(中文版)(2021年4期)2021-02-12
河北理科教学研究(2020年3期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
科学(2020年1期)2020-08-24
中学生数理化·中考版(2017年10期)2017-04-23

