对圆锥曲线一共性之推广
2018-11-29 07:10魏子贺
数理化解题研究 2018年31期
魏子贺
(河北省乐亭第一中学高三年级 063600)
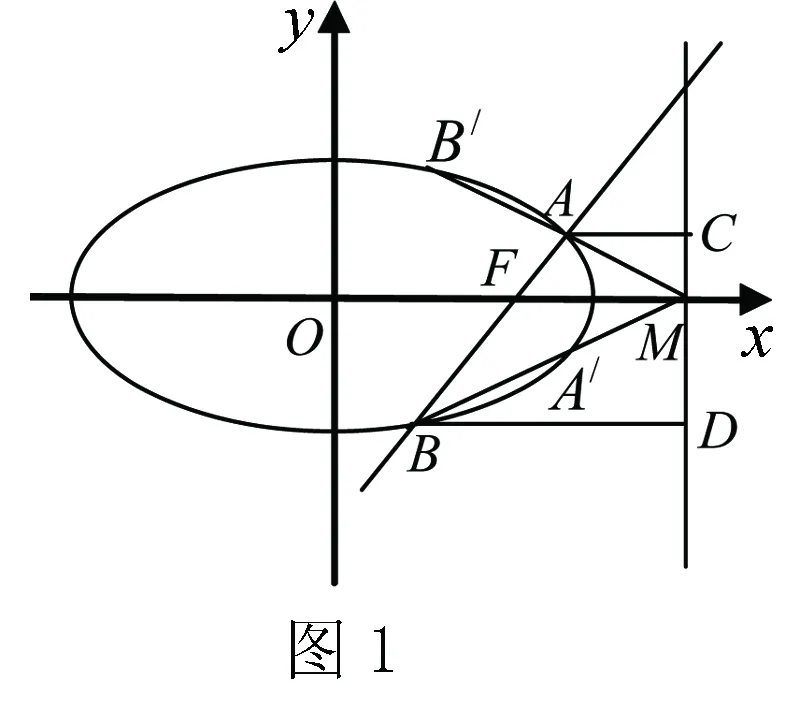
设圆锥曲线的一个焦点为F,相应准线l交焦点所在的对称轴(图(1)中的x轴)于点M,过F的直线交圆锥曲线于A,B两点.则MF是∠AMB的角平分线(特别地当圆锥曲线为双曲线时,要满足A,B两点落在双曲线的同一支.否则落在左右两支上时∠AMF,∠BMF互补).
“性质”的成立必须在F为焦点且M为相应准线与对称轴的交点的条件下(这一性质是2018年高考全国卷一19题第2问的证明,所以此处不再证明),如果改变这一条件,仅让这两点存在某种特定的内在联系,我们可得到如下一组推论.
推论1 已知抛物线y2=2px(p>0)过定点F′(m,0)(m≠0)的直线交抛物线于A,B两点,则对称轴上存在定点M′(-m,0)使得下面结论成立:(1)当m>0时,∠AM′F′=∠BM′F′;(2)当m<0时,∠AM′F′+∠BM′F′=180°.
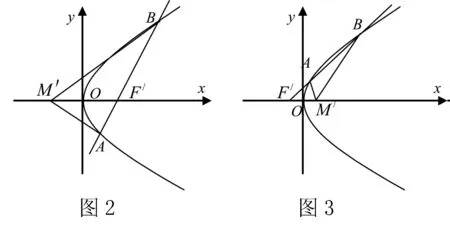
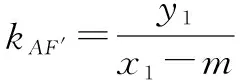
当m>0时结合图(2)可得∠AM′F′=∠BM′F′;当m<0时结合图(3)可得∠AM′F′+∠BM′F′=180°.若AB的斜率不存在,则必须满足m>0,此时命题成立.
类似的结论在椭圆和双曲线中仍然成立,见下面推论2,推论3.

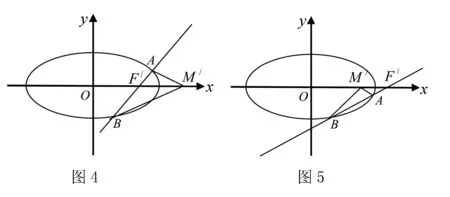
证明当AB的斜率存在时(斜率不存在时成立,略去不证),设A(x1,y1),B(x2,y2),AB所在直线方程为y=k(x-m)(k≠0),将其代入椭圆方程并整理得(b2+a2k2)x2-2ma2k2x+(a2k2m2-a2b2)=0.
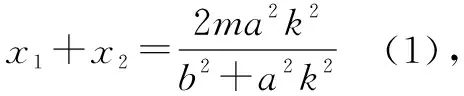
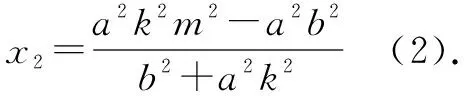

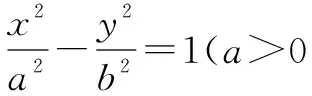
推论3的证明与推论1、2思路类似,在此不在给出.以上通过对2018年全国卷一解析几何解答题的分析给出了三个相关推论,希望对读者以后的学习有所帮助.
猜你喜欢
中学数学研究(江西)(2022年5期)2022-05-08
中学数学研究(江西)(2019年6期)2019-07-08
中学生数理化·七年级数学人教版(2017年10期)2017-04-23
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16
福建中学数学(2016年2期)2016-10-19
数学大王·低年级(2016年10期)2016-09-10
中学数学杂志(2015年9期)2015-01-01
福建中学数学(2013年1期)2013-03-06
中学数学研究(2008年3期)2008-12-09
中学生数理化·七年级数学北师大版(2008年6期)2008-10-22

