定义在R的奇函数可以任性使用f(0)=0
孟维帅
(辽宁省大连市庄河市第五高级中学)
定义在R的奇函数可以任性使用f(0)=0
孟维帅
(辽宁省大连市庄河市第五高级中学)

就上述问题,不由让笔者引起思考,倘若函数在x=0处有定义,一般的来说,定义在R上的奇函数难道就可以任性地使用f(0)=0来求参吗?笔者认为,结合具体实例来研究这个问题不失为一个好办法.
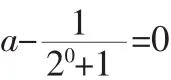
通过例1,发现定义在R上的奇函数可以任性的使用f(0)=0来求出参数a,但是一个例子的佐证似乎显得有些苍白,因此笔者再选一例来讨论定义在R上的奇函数是否任性的使用f(0)=0来求参.

当a=1时,函数f(x)=ex-e-x.
此时f(-x)=e-x-ex,显然f(x)+f(-x)=0.
当a=-1时,函数f(x)=e-x-ex,
此时f(-x)=ex-e-x,显然f(x)+f(-x)=0.
综上,a=±1都会使得函数f(x)为奇函数.
例2似乎进一步巩固了例1的说法,即定义在R的奇函数可利用f(0)=0来求解析式中的参数,讨论也仿佛到了尾声,结论好像已如磐石那般坚定,然而笔者却始终心存疑虑,并开始寻找定义域为R的反例,最终寻得一例,并予以说明:
例3 已知函数f(x)=ax2+(a-1)x+a2-a(a∈R)为奇函数,求实数a的值.
解法一:不难看出,函数f(x)是定义域为R的奇函数,利用f(0)=0可得a2-a=0,解得a=0或a=1.
当a=0时,f(x)=-x,此时f(-x)=x,于是f(x)+f(-x)=0,
由奇函数的定义可知,函数f(x)为奇函数.
当a=1时,f(x)=x2,此时f(-x)=f(x),函数f(x)为偶函数,而并非奇函数.
此例是以简单的多项式函数来构造成功反例,推翻了定义在R的奇函数可任性使用f(0)=0来求解析式中的参数,例子虽然简单但是足以说明问题,即使是定义在R上的奇函数,也不可以任性地使用f(0)=0来求参数.
通过对三道例题的分析,例1和例2说明f(0)=0确实是为求定义域为R上的奇函数中的参数问题提供了便利,但同时例3警示此类做法的风险,同时也指出此类方法检验的必要性.
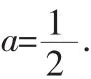
·编辑 鲁翠红

