例析框图三大交汇问题
唐洵

随着课改的深入,高考对考生的能力要求正在不断提升,在交汇处命制试题也成为出题老师的一大重要手段.因此,当同学们面对数学问题时,应当学会多方位思考,建构系统的知识结构,做到“窥一斑而见全豹,做一题而解一类”.那么算法与程序框图的试题有哪些常见交汇呢?
交汇一、携手函数,翩翩起舞
题型介绍:框图与函数的交汇主要体现为两方面内容:一是利用条件结构,将分段函数融人框图之中,求函数的值或值域,此时应先从框图中抽象出分段函数的具体形式,再求解函数在各自段上的值域,最后进行综合;二是利用条件结构或循环结构,通过判断函数的性质,筛选函数,此时应当紧抓函数性质的判定方法,如函数的奇偶性,可通过定义法或图象法进行判定等.
例1 某程序框图如图1所示,现有以下六个函数,任选一个函数输入,则函数可以输出的个数为()
(1)f(x)=x;(2)f(x)=lgx;(3)f(x)=ex;(4)f(x)=sinx/x(5)f(x)=x/ln/x(6)f(x)=x2COSx.
A.1
B.2
C.3
D.4
分析 f(x)+f(-x)=0 f(-x)=-f(x) 函数为奇函数;因此先判断函数是否为奇函数,再判断函数是否存在零点.
解析 由程序框图可知,要使得函数输出,必须满足f(x)是奇函数并且f(x)在定义域上存在零点.易知f(x)=x符合输出的条件;f(x)=lgx,f(x)=e x均为非奇非偶函数;f(z)=sinx/x为奇函数且x=π为该函数的一个零点,符合输出的条件;f(x)=x/ln|x|是奇函数,由函数图象可知,该函数在其定义域内无零点;f(x)=x2 COSx为偶函数;故满足输出条件的仅有f(x)=x和f(x)=sinx/x所以任选一个函数输入,则函数可以输出的个数为2,故选B.
点评 本例将函数的性质与程序框图相挂钩,其解题关键在于看懂程序框图的内涵及选择正确的判定方法.如函数的奇偶性常见的判定方法有三种:一是定义法,即利用f(-x)与f;(x)的关系进行判断;二是图象法,即利用所给函数的图象是否关于原点或y轴对称进行合理判断,一般用于基本初等函数或函数的识图问题中;三是结论法,如“奇函数X奇函数一偶函数,奇函数×偶函数一奇函数”等常用二级结论进行判定.在平时的学习过程中应注意积累.
交汇二、相约数列,结伴而行
题型介绍:框图与数列的交汇多种多样,其一般以循环结构为主线,可以考查特殊数列的求值、等差数列或等比数列的前n项和、分组求和法、裂项相消法等诸多内容.常见的利用循环结构求值就是一种特殊的框图与数列的交汇性试题.
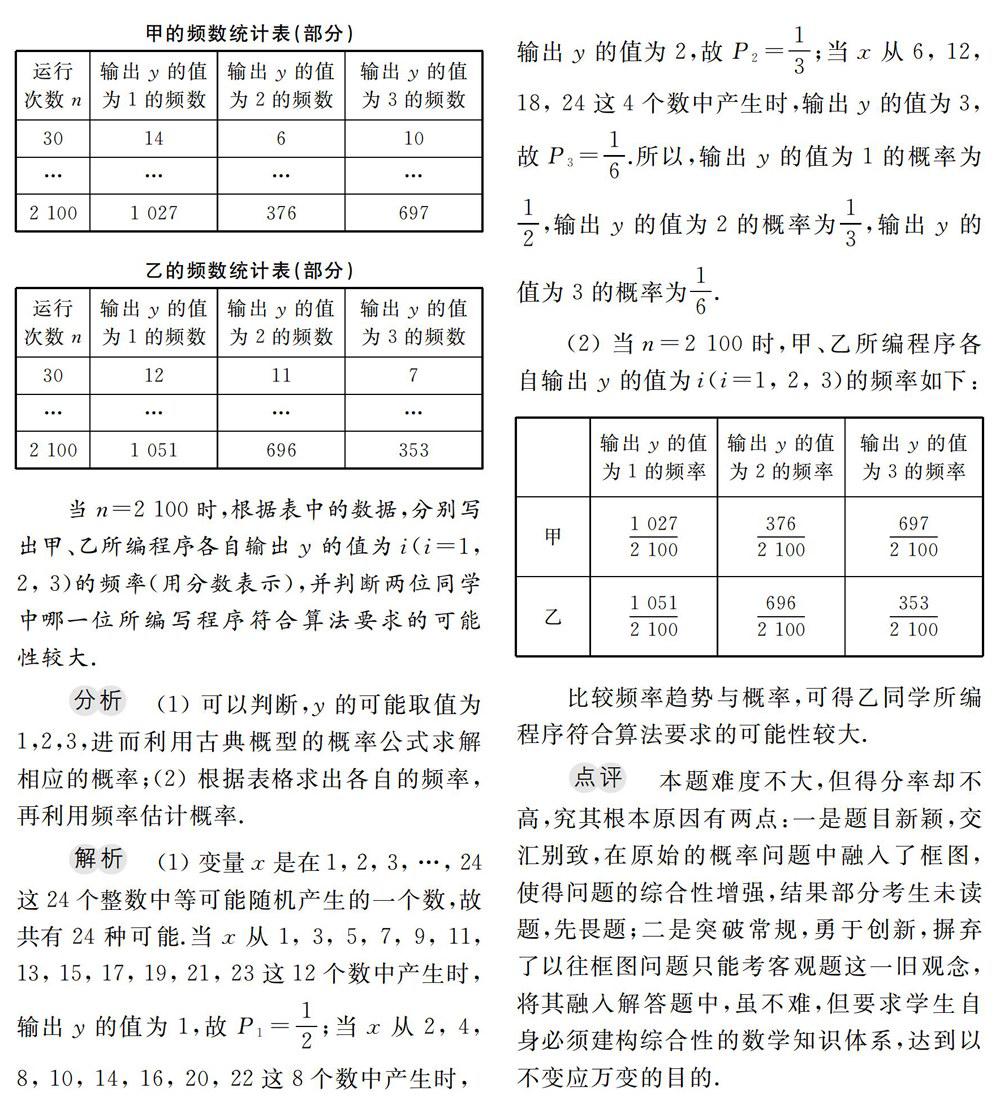
例2执行如图2的程序框图,如果输入p=10,则输出的S=____.
分析 运行第一次,S=O+1/2,n=2;运行第二次,S=O+1/2十1/22,n=3;运行第三次,s=o+1/+1/2+1/221/23,n=4;…;以此类推,可知该程序的功能是实现等比数列的求和,此时应当注意循环结构的终止条件.
解析 运行该程序,可知该程序输出的s=o+1/+1/2+……1/2,由等比数列求和公式可知S=511/512
点评 数列与框图的交汇在高考中屡见不鲜,处理此类问题往往有两种方法:一是按部就班,运行程序,根据框图提示,一步一步地运行程序,得到相应答案,此法一般在框图步骤较少时使用;二是归纳推理,根据框图提示列出前几项,观察规律,看清该框图实现的功能是求数列中的项还是求和,进而套用相应的数列公式进行求解.交汇三、联袂概率,新颖别致
例3 某算法的程序框图如图3所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(1)分别求出按程序框圖正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=l,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
分析 (l)可以判断,y的可能取值为1,2,3,进而利用古典概型的概率公式求解相应的概率;(2)根据表格求出各自的频率,再利用频率估计概率,
解析 (l)变量x是在l,2,3.….24这24个整数中等可能随机产生的一个数,故共有24种可能.当x从1,3,5,7,9,II,13,15,17,19,21,23这12个数中产生时,输出y的值为1,故P1=1/2;当x从2,4,8,10,14,16,20,22这8个数中产生时,输出y的值为2,故P2=1/3;当x从6, 12,18,24这4个数中产生时,输出y的值为3,故P3=1/6.所以,输出y的值为1的概率为1/2,输出y的值为2的概率为1/3,输出y的值为3的概率为1/6.
(2)当n=2100时,甲、乙所编程序各自输出y的值为i(i=l,2,3)的频率如下:
比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大.
点评 本题难度不大,但得分率却不高,究其根本原因有两点:一是题目新颖,交汇别致,在原始的概率问题中融入了框图,使得问题的综合性增强,结果部分考生未读题,先畏题;二是突破常规,勇于创新,摒弃了以往框图问题只能考客观题这一旧观念,将其融人解答题中,虽不难,但要求学生自身必须建构综合性的数学知识体系,达到以不变应万变的目的.

